/Szkoła średnia/Równania/Wykładnicze/Z parametrem

Zadanie nr 4321602

Znajdź zbiór tych wartości parametru 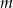m dla których równanie 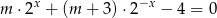m ⋅2x + (m + 3) ⋅2−x − 4 = 0 ma co najmniej jedno rozwiązanie.

Wersja PDF

Rozwiązanie

Podstawiając 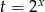x t = 2 mamy równanie

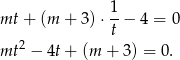
1 mt + (m + 3)⋅ -− 4 = 0 t mt2 − 4t+ (m + 3 ) = 0.

Zapisując podstawienie 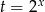t = 2x w postaci

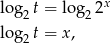
x log 2t = log2 2 log t = x, 2

widzimy, że równanie będzie miało rozwiązanie, gdy powyższe równanie kwadratowe ma co najmniej jedno rozwiązanie dodatnie.

Sprawdźmy najpierw co się dzieje, gdy równanie nie jest kwadratowe, tzn. dla 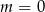m = 0 . Mamy wtedy

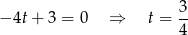
− 4t+ 3 = 0 ⇒ t = 3- 4

i jest OK.

Jeżeli równanie jest kwadratowe, to na początek sprawdźmy kiedy równanie ma pierwiastki

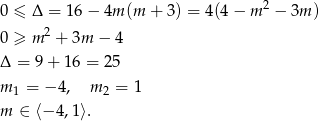
2 0 ≤ Δ = 16 − 4m (m + 3) = 4(4 − m − 3m ) 0 ≥ m 2 + 3m − 4 Δ = 9 + 16 = 25 m 1 = − 4, m 2 = 1 m ∈ ⟨− 4,1⟩.

Tak naprawdę z tego przedziału powinniśmy wyrzucić 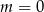m = 0 , ale nie robimy tego, bo już sprawdziliśmy, że dla 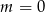m = 0 jest OK.

Musimy teraz ustalić kiedy przynajmniej jeden pierwiastek jest dodatni. Jest to dość nieprzyjemny warunek do sprawdzania – o wiele łatwiej jest odpowidzieć na pytanie przeciwne: kiedy pierwiastki są niedodatnie. Na mocy wzorów Viéte’a tak będzie, gdy

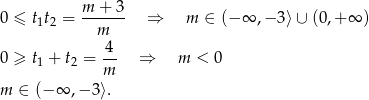
m + 3 0 ≤ t1t2 = ------ ⇒ m ∈ (− ∞ ,− 3⟩∪ (0,+ ∞ ) m 0 ≥ t + t = 4- ⇒ m < 0 1 2 m m ∈ (− ∞ ,− 3⟩.

Zatem będziemy mieli jeden pierwiastek dodatni gdy (patrzymy też na warunek z 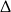Δ -ą!)

m ∈ (− 3 ,1 ⟩.

 
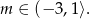
Odpowiedź: m ∈ (− 3,1⟩

Wersja PDF