/Szkoła średnia/Geometria/Planimetria/Trójkąt/Równoramienny/Kąty

Zadanie nr 5108498

W trójkącie równoramiennym środkowe ramion są prostopadłe. Oblicz cosinus kąta między ramionami.

Wersja PDF

Rozwiązanie

Sposób I

Zaczynamy od rysunku.

PIC

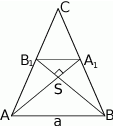
Szukany cosinus będziemy chcieli wyliczyć z twierdzenia cosinusów zastosowanego do trójkąta 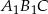A 1B 1C . Aby móc to zrobić oznaczmy długość podstawy 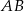AB przez a (równie dobrze możemy ustalić, że jest to 1). Na mocy twierdzenia Talesa (lub podobieństwa trójkątów)

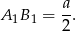
A B = a-. 1 1 2

Stosując twierdzenie Pitagorasa do trójkąta 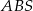ABS mamy

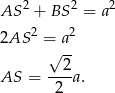
2 2 2 AS + BS = a 2AS 2 = a 2 √ -- --2- AS = 2 a.

Ponieważ punkt przecięcia się środkowych dzieli każdą z nich w stosunku 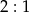2 : 1 (licząc od wierzchołka), to

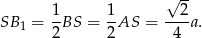
√ -- SB 1 = 1-BS = 1AS = --2a. 2 2 4

Stosujemy teraz twierdzenie Pitagorasa do trójkąta 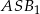ASB 1

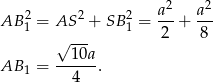
2 2 AB 2= AS 2 + SB 2= a--+ a-- 1 √ --- 1 2 8 10a AB 1 = ------. 4

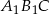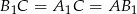No i w końcu możemy zastosować twierdzenie cosinusów do trójkąta A B C 1 1 (korzystamy z faktu, że B1C = A 1C = AB 1 ).

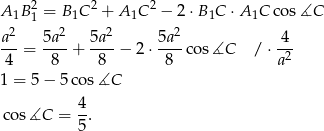
A B2 = B C2 + A C2 − 2 ⋅B C ⋅A C cos ∡C 1 1 1 1 1 1 a2- 5a2- 5a2- 5a-2 4-- 4 = 8 + 8 − 2 ⋅ 8 cos ∡C / ⋅ a2 1 = 5 − 5 cos∡C 4- cos ∡C = 5.

Sposób II

Znowu zaczynamy od rysunku, ale tym razem użyjemy do rozwiązania wektory.

PIC

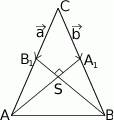
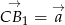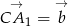Oznaczmy → → CB 1 = a oraz → → CA 1 = b . Możemy ponadto przyjąć, że oba te wektory mają długość 1, czyli

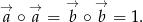
→ → → → a ∘ a = b ∘ b = 1.

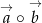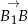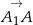To co musimy zrobić, to wyliczyć → → a ∘ b – ponieważ wektory mają długość 1, jest to dokładnie cosinus kąta między nimi. Aby to zrobić wyliczymy wektory B→ B 1 i A →A 1 i skorzystamy z faktu, że są one prostopadłe. Liczymy

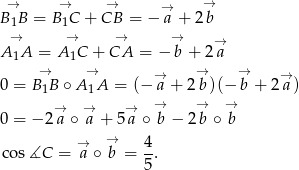
→ → → → → B 1B = B1C + CB = − a + 2 b → → → → → A 1A = A 1C + CA = − b + 2a → → → → → → 0 = B1B ∘ A 1A = (− a + 2 b)(− b + 2a ) → → → → → → 0 = − 2a ∘ a + 5 a ∘ b − 2 b ∘ b → → 4 cos∡C = a ∘ b = -. 5

 
Odpowiedź: 4 5

Wersja PDF