Zadanie nr 9512931
Pokazać, że dla każdej liczby całkowitej  liczba
liczba 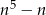 jest podzielna przez 5.
jest podzielna przez 5.
Rozwiązanie
Sposób I
Rozkładamy podane wyrażenie
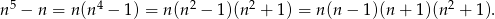
Jeżeli liczba  daje przy dzieleniu przez 5 resztę 0,1 lub 4, to jedna z liczb w pierwszych trzech nawiasach dzieli się przez 5. Jeżeli natomiast
daje przy dzieleniu przez 5 resztę 0,1 lub 4, to jedna z liczb w pierwszych trzech nawiasach dzieli się przez 5. Jeżeli natomiast 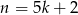 lub
lub 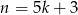 to
to
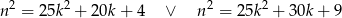
i liczba 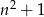 dzieli się przez 5.
dzieli się przez 5.
Sposób II
Robimy podobnie jak poprzednio, ale używamy odrobinę innego rozkładu.
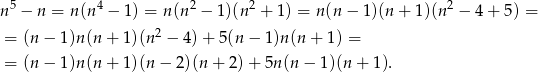
Pierwszy składnik jest iloczynem 5 kolejnych liczb całkowitych jest więc podzielny przez 5. Drugi dzieli się przez 5 w oczywisty sposób.
Sposób III
Zadanie możemy też rozwiązać indukcyjnie, ale będziemy potrzebować wzoru dwumianowego Newtona dla 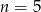
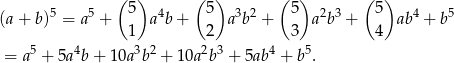
Zakładamy indukcyjnie, że 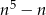 dzieli się przez 5 i liczymy
dzieli się przez 5 i liczymy
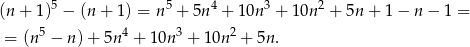
Wyrażenie w nawiasie dzieli się przez 5 z założenia indukcyjnego, reszta też, więc wykazaliśmy tezę dla 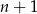 .
.
Zadanie jest szczególnym przypadkiem tzw. małego twierdzenia Fermata: jeżeli 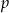 jest liczbą pierwszą, to
jest liczbą pierwszą, to 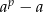 dzieli się przez
dzieli się przez 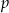 .
.

