W ostrosłupie prawidłowym czworokątnym ściana boczna o polu równym 10 jest nachylona do płaszczyzny podstawy pod kątem 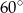 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy czworokątny
Oblicz objętość i pole powierzchni całkowitej ostrosłupa prawidłowego czworokątnego, w którym krawędź podstawy ma długość 2, a krawędź boczna długość 6.
Oblicz objętość i pole powierzchni całkowitej ostrosłupa prawidłowego czworokątnego, w którym krawędź boczna ma długość 8, a krawędź podstawy ma długość 2.
Oblicz objętość i pole powierzchni całkowitej ostrosłupa prawidłowego czworokątnego, w którym krawędź podstawy ma długość 4, a krawędź boczna długość 10.
W ostrosłupie prawidłowym czworokątnym 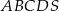 o podstawie
o podstawie 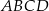 wysokość jest równa 5, a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę
wysokość jest równa 5, a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę 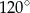 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Dany jest ostrosłup prawidłowy czworokątny. Wysokość ściany bocznej tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 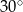 i ma długość równą 6 (zobacz rysunek).
i ma długość równą 6 (zobacz rysunek).
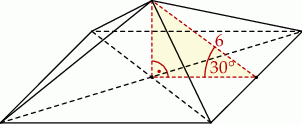
Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.
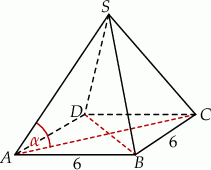
Długość krawędzi podstawy ostrosłupa prawidłowego czworokątnego jest równa 6. Pole powierzchni całkowitej tego ostrosłupa jest cztery razy większe od pola jego podstawy. Kąt  jest kątem nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny podstawy (zobacz rysunek). Oblicz cosinus kąta
jest kątem nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny podstawy (zobacz rysunek). Oblicz cosinus kąta  .
.
Ostrosłup prawidłowy czworokątny przecięto płaszczyzna przechodzącą przez krawędź podstawy i przecinającą przeciwległe krawędzie boczne w punktach jednakowo odległych od wierzchołka ostrosłupa. Przekrój ten jest trapezem o podstawach długości 12 i 8. Oblicz pole tego przekroju, jeżeli wysokość ostrosłupa ma długość 18.
Dany jest ostrosłup prawidłowy czworokątny 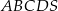 o podstawie
o podstawie 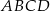 . Krawędź podstawy tego ostrosłupa ma długość
. Krawędź podstawy tego ostrosłupa ma długość  . Ściana boczna jest nachylona do płaszczyzny podstawy pod kątem o mierze
. Ściana boczna jest nachylona do płaszczyzny podstawy pod kątem o mierze  takim, że
takim, że 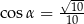 . Przez krawędź
. Przez krawędź 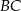 podstawy ostrosłupa poprowadzono płaszczyznę
podstawy ostrosłupa poprowadzono płaszczyznę 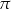 prostopadłą do ściany bocznej
prostopadłą do ściany bocznej 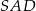 . Sporządź rysunek tego ostrosłupa, zaznacz na rysunku przekrój wyznaczony przez płaszczyznę
. Sporządź rysunek tego ostrosłupa, zaznacz na rysunku przekrój wyznaczony przez płaszczyznę 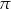 i nazwij figurę, która jest tym przekrojem. Oblicz pole otrzymanego przekroju.
i nazwij figurę, która jest tym przekrojem. Oblicz pole otrzymanego przekroju.
Objętość ostrosłupa prawidłowego czworokątnego 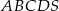 o podstawie
o podstawie 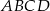 jest równa 224, a promień okręgu opisanego na podstawie
jest równa 224, a promień okręgu opisanego na podstawie 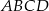 jest równy
jest równy 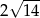 . Oblicz cosinus kąta między wysokością tego ostrosłupa i jego ścianą boczną.
. Oblicz cosinus kąta między wysokością tego ostrosłupa i jego ścianą boczną.
Dany jest ostrosłup prawidłowy czworokątny 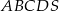 o podstawie
o podstawie 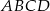 . Pole trójkąta
. Pole trójkąta 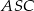 jest równe 120, a cosinus kąta
jest równe 120, a cosinus kąta 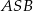 jest równy
jest równy 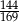 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.
Dany jest ostrosłup prawidłowy czworokątny 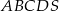 o podstawie
o podstawie 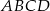 . W trójkącie równoramiennym
. W trójkącie równoramiennym 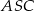 stosunek długości podstawy do długości ramienia jest równy
stosunek długości podstawy do długości ramienia jest równy 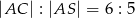 . Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
. Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
Wysokość ostrosłupa prawidłowego czworokątnego jest 2 razy dłuższa od krawędzi jego podstawy. Przez przekątną podstawy i środek rozłącznej z nią krawędzi bocznej poprowadzono płaszczyznę. Oblicz pole otrzymanego przekroju, wiedząc, że krawędź podstawy ostrosłupa ma długość  .
.
Wysokość ostrosłupa prawidłowego czworokątnego jest 2,5 razy dłuższa od krawędzi jego podstawy. Przez przekątną podstawy i środek rozłącznej z nią krawędzi bocznej poprowadzono płaszczyznę. Oblicz pole otrzymanego przekroju, wiedząc, że krawędź podstawy ostrosłupa ma długość  .
.
Objętość ostrosłupa prawidłowego czworokątnego jest równa 384. Wysokość ściany bocznej tego ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze  taki, że
taki, że 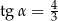 .
.
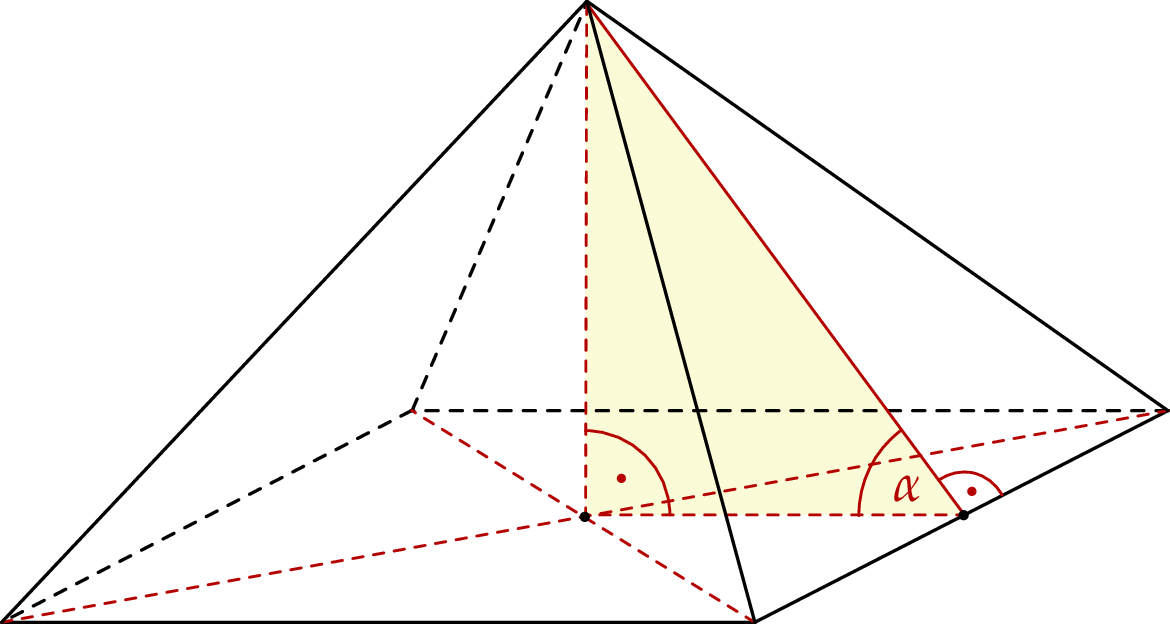
Oblicz wysokość ściany bocznej tego ostrosłupa.
W ostrosłupie prawidłowym czworokątnym o krawędzi podstawy 18 cm, kąt między wysokościami przeciwległych ścian bocznych ma miarę 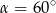 . Oblicz pole powierzchni bocznej tego ostrosłupa. Wykonaj odpowiedni rysunek i zaznacz kąt
. Oblicz pole powierzchni bocznej tego ostrosłupa. Wykonaj odpowiedni rysunek i zaznacz kąt  .
.
W ostrosłupie prawidłowym czworokątnym o krawędzi podstawy 12 cm, kąt między wysokościami przeciwległych ścian bocznych ma miarę 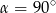 . Oblicz pole powierzchni bocznej tego ostrosłupa. Wykonaj odpowiedni rysunek i zaznacz kąt
. Oblicz pole powierzchni bocznej tego ostrosłupa. Wykonaj odpowiedni rysunek i zaznacz kąt  .
.
Odległość środka podstawy ostrosłupa prawidłowego czworokątnego od krawędzi bocznej równa się  , a kąt płaski ściany bocznej przy wierzchołku ostrosłupa równa się
, a kąt płaski ściany bocznej przy wierzchołku ostrosłupa równa się 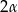 . Oblicz wysokość ostrosłupa.
. Oblicz wysokość ostrosłupa.
W ostrosłupie prawidłowym czworokątnym wysokości przeciwległych ścian bocznych, poprowadzone z wierzchołka ostrosłupa, są do siebie prostopadłe.
- Oblicz sinus kąta nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy.
- Jakim procentem objętości sześcianu, którego krawędź ma długość równą długości krawędzi podstawy danego ostrosłupa, jest objętość tego ostrosłupa?
Krawędź boczna ostrosłupa prawidłowego czworokątnego jest nachylona do płaszczyzny podstawy pod kątem  takim, że
takim, że 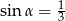 . Oblicz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
. Oblicz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.

