Zadanie nr 7627047
Udowodnij, że jeżeli liczby 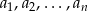 , gdzie
, gdzie 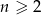 , tworzą ciąg arytmetyczny i żadna z nich nie jest zerem, to
, tworzą ciąg arytmetyczny i żadna z nich nie jest zerem, to
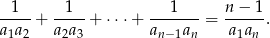
Rozwiązanie
Sposób I
Uzasadnimy podaną równość indukcyjnie.
Dla 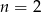 mamy oczywistą równość
mamy oczywistą równość
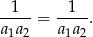
Załóżmy, że wzór ten jest prawdziwy dla liczby  , pokażemy jego prawdziwość dla liczby
, pokażemy jego prawdziwość dla liczby 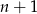 . Liczymy
. Liczymy
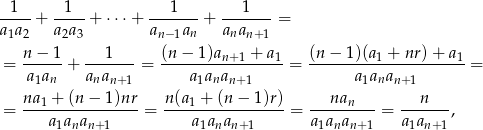
co kończy dowód indukcyjny.
Sposób II
Tym razem będziemy się wzorować na znanym sposobie liczenia sumy
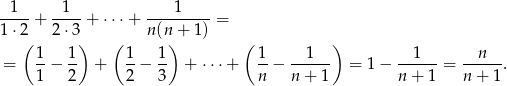
Zauważmy, że
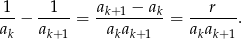
Zatem
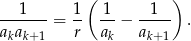
Przekształćmy teraz sumę z treści zadania