/Szkoła podstawowa/Egzamin ósmoklasisty/Egzamin 2019/Próbne testy
Próbny Egzamin Ósmoklasisty
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 13 kwietnia 2019 Czas pracy: 100 minut
Firma kurierska przyjmuje wyłącznie paczki, których wymiary spełniają następujące warunki:
– wysokość paczki nie może przekraczać 80 cm;
– szerokość paczki nie może przekraczać 60 cm;
– obwód paczki, zdefiniowany wzorem
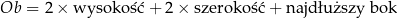
nie może przekraczać 3 m.
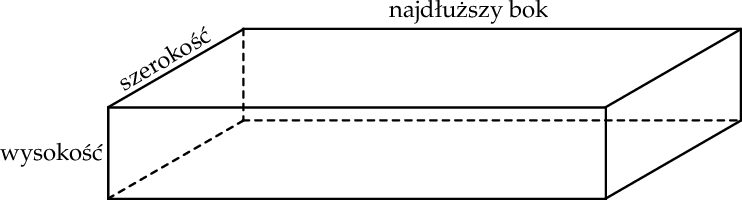
Jeżeli paczka o wymiarach
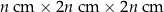 spełnia warunki wysyłki, to największa możliwa wartość
spełnia warunki wysyłki, to największa możliwa wartość  jest równa
jest równa A) 37,5 B) 40 C) 60 D) 30
Kierowca samochodu dostawczego zanotował w tabeli informacje o 6 wyjazdach służbowych.
| L. p. | Liczba przejechanych kilometrów | Czas podróży |
| 1. | 170 | 2 h 50 min |
| 2. | 160 | 2 h 20 min |
| 3. | 120 | 2 h |
| 4. | 150 | 2 h 20 min |
| 5. | 310 | 5 h 10 min |
| 6. | 190 | 3 h 10 min |
Na podstawie informacji zawartych w powyższej tabeli wybierz zdanie prawdziwe.
A) Kierowca w ciągu jednego wyjazdu przejeżdżał średnio 180 km.
B) Trzy pierwsze wyjazdy trwały dłużej, niż trzy kolejne.
C) Podczas dwóch pierwszych wyjazdów kierowca przejechał 30% łącznej liczby kilometrów przejechanych podczas 6 wyjazdów.
D) Średnia prędkość podczas każdego z wyjazdów wyniosła 60 km/h.
Która równość jest fałszywa? Wybierz odpowiedź spośród podanych.
A) 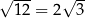 B)
B) 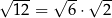 C)
C) 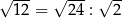 D)
D) 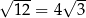
W X edycji konkursu recytatorskiego wzięło udział 140 dziewcząt i 112 chłopców. W XI edycji tego konkursu wzięła udział ta sama liczba osób, ale liczba dziewcząt zmalała o 20%. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W X edycji konkursu wzięło udział o 20% dziewcząt więcej niż w XI edycji. | P | F |
| Liczba chłopców w XI edycji konkursu wzrosła w stosunku do liczby chłopców w X edycji o 20%. | P | F |
Pewna agencja reklamowa przygotowała zestawy promocyjne, które zawierały długopisy, ołówki i notesy. W każdym zestawie była taka sama liczba długopisów, ołówków i notesów, a łącznie we wszystkich zestawach znalazło się 225 długopisów, 300 ołówków i 150 notesów.
Ile maksymalnie przygotowano zestawów reklamowych? Wybierz odpowiedź spośród podanych.
A) 90 B) 75 C) 50 D) 25
Wykres przedstawia zależność drogi przebytej przez samochód jadący z miasta 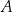 do miasta
do miasta 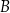 w zależności od czasu jazdy.
w zależności od czasu jazdy.
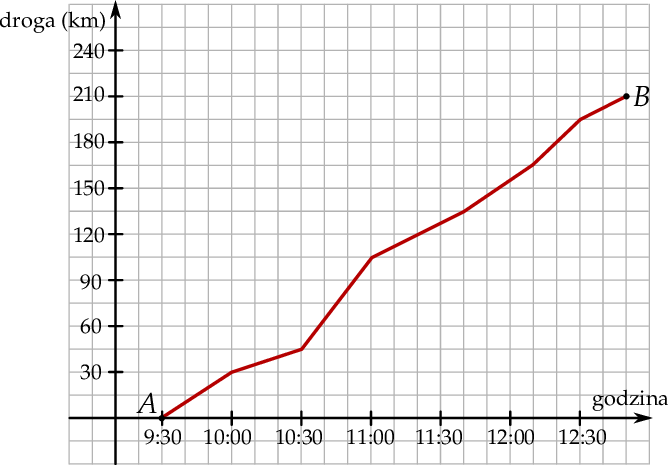
Zaznacz P, jeśli zdanie jest prawdziwe, lub zaznacz F – jeśli jest fałszywe.
| Samochód przejechał drugą połowę trasy szybciej niż pierwszą połowę. | P | F |
| Pół godziny przez zakończeniem podróży samochód miał jeszcze do przejechania 30 km. | P | F |
Jeden litr to 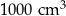 . Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
. Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Jeden metr sześcienny to A/B litrów.
A) 10000 B) 1000
Jeden  to C/D litra.
to C/D litra.
C) 0,0001 D) 0,000001
Dwie proste równoległe 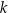 i
i 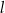 przecięto prostymi
przecięto prostymi 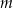 i
i  w sposób przedstawiony na rysunku.
w sposób przedstawiony na rysunku.
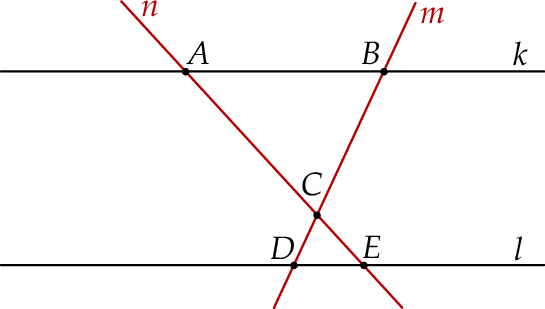
Czy trójkąty 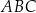 i
i 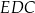 są przystające? Wybierz odpowiedź T albo N oraz jej uzasadnienie spośród zdań oznaczonych literami A–D.
są przystające? Wybierz odpowiedź T albo N oraz jej uzasadnienie spośród zdań oznaczonych literami A–D.
| Tak | Nie |
| ponieważ | |
| A) | te trójkąty mają wspólny wierzchołek. |
| B) | te trójkąty mają boki różnej długości. |
| C) | te trójkąty mają odpowiednie kąty równej miary. |
| D) | te trójkąty mają boki równoległe. |
Adam i Wojtek mają razem 82 cukierki. Jeżeli każdy z chłopców zje 29 cukierków, to Adam będzie miał trzy razy mniej cukierków niż Wojtek.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jeżeli Wojtek odda Adamowi 6 cukierków, to chłopcy będą mieli taką samą liczbę cukierków. | P | F |
| Jeżeli każdy z chłopców zje 23 cukierki, to Wojtek będzie miał dwa razy więcej cukierków niż Adam. | P | F |
Po dodaniu do zestawu liczb: 10, 4, 5, 9, 12 jednej liczby średnia liczb zmniejszyła się o 1.
Którą z poniższych liczb dopisano? Wybierz odpowiedź spośród podanych.
A) 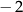 B)
B) 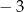 C) 2 D) 3
C) 2 D) 3
Uczniowie na zimowisku zostali podzielni na 4 grupy. Tabela zawiera informację o liczbie uczniów w poszczególnych grupach z podziałem ze względu na ich wiek.
| Wiek | Grupa I | Grupa II | Grupa III | Grupa IV |
| 10 lat | 20 | 10 | 30 | 20 |
| 11 lat | 30 | 10 | 20 | 0 |
| 12 lat | 40 | 30 | 30 | 20 |
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo, że losowo wybrany uczeń grupy ma 12 lat jest największe, gdy ucznia losujemy z grupy II. | P | F |
| Prawdopodobieństwo, że losowo wybrany uczeń grupy ma mniej niż 12 lat jest najmniejsze, gdy ucznia losujemy z grupy II. | P | F |
Dokończ zdanie, wybierając odpowiedź spośród podanych.
Miara kąta  zaznaczonego na rysunku jest równa
zaznaczonego na rysunku jest równa
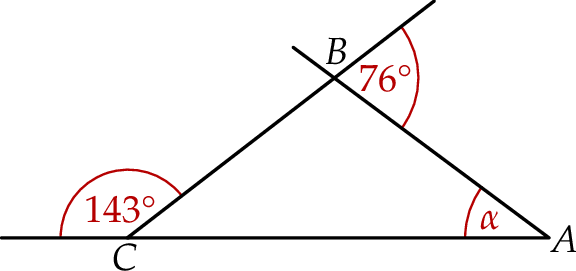
A) 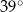 B)
B) 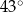 C)
C) 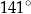 D)
D) 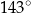
Do pomalowania wszystkich ścian graniastosłupa czworokątnego zużyto 30 mililitrów farby o wydajności 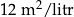 .
.
Dokończ zdanie, wybierając odpowiedź spośród podanych. Pole powierzchni tego graniastosłupa jest równe
A) 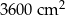 B)
B) 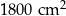 C)
C) 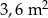 D)
D) 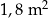
Na rysunku przedstawiono równoległobok 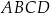
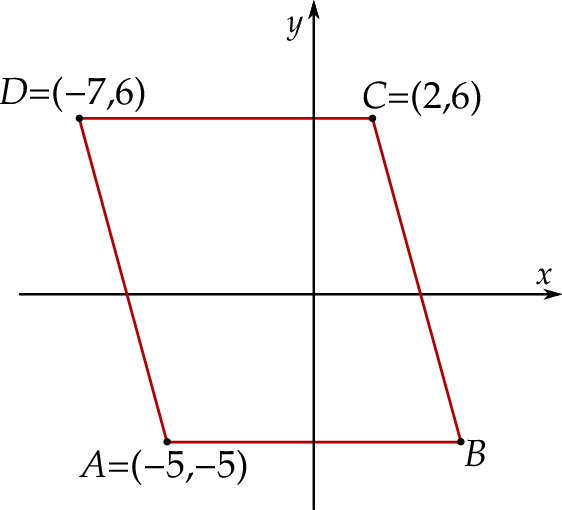
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Pole równoległoboku 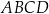 jest równe A/B .
jest równe A/B .
A) 99 B) 80
Wierzchołek 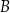 równoległoboku
równoległoboku 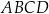 ma współrzędne C/D .
ma współrzędne C/D .
C) 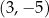 D)
D) 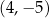
Na rysunku podano wymiary trzech prostopadłościennych pojemników.

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Objętość pojemnika nr 2 jest dwa razy mniejsza od objętości pojemnika nr 1. | P | F |
| Objętość pojemnika nr 3 jest dwa razy większa od objętości pojemnika nr 1. | P | F |
Każdy z 240 uczniów pewnej szkoły otrzymał 3 lub 4 darmowe bilety do kina. W sumie rozdano 880 biletów. Ilu uczniów otrzymało 3, a ilu 4 bilety? Zapisz obliczenia.
Oblicz pole trójkąta, którego wymiary podano na rysunku.

Kasia napisała na tablicy 6 kolejnych wielokrotności liczby 9. Uzasadnij, że suma pierwszych trzech z tych liczb jest o 81 mniejsza od sumy trzech ostatnich.
Przekątna 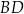 prostokąta
prostokąta 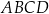 ma długość 10 i dzieli prostokąt na dwa trójkąty prostokątne, w których stosunek przyprostokątnych jest równy
ma długość 10 i dzieli prostokąt na dwa trójkąty prostokątne, w których stosunek przyprostokątnych jest równy  . Oblicz obwód prostokąta. Zapisz obliczenia.
. Oblicz obwód prostokąta. Zapisz obliczenia.
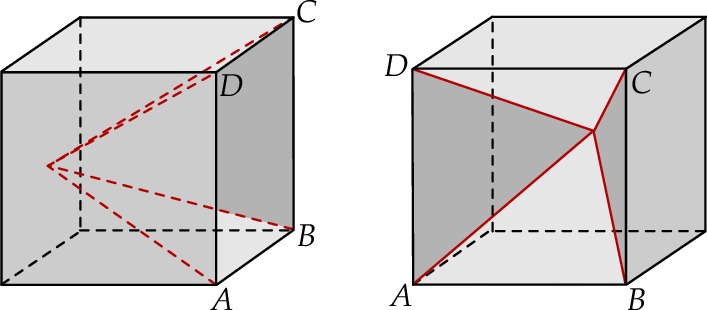
Z drewnianego sześcianu o krawędzi długości 6 cm wycięto ostrosłup prawidłowy czworokątny o wysokości równej krawędzi sześcianu. Otrzymano w ten sposób bryłę, której widok z dwóch stron przedstawiono na rysunku. Jaką objętość ma ta bryła? Zapisz obliczenia.
Na schematycznym planie miasta zaznaczono położenie domów trzech koleżanek: Kasi, Uli i Ewy. Odległość między domami Kasi i Uli jest równa 900 m, a odległość między domami Uli i Ewy jest równa 1,2 km. Oblicz odległość (mierzoną w linii prostej) między domami Kasi i Ewy. Zapisz obliczenia.