Zamawiając pizzę mamy do wyboru 12 dodatków, 2 rodzaje ciasta i 3 rodzaje sosów. Na ile sposobów możemy zamówić pizzę jeżeli zdecydowaliśmy się wybrać jeden dodatek główny i jeden dodatek pomocniczy (różny od głównego), oraz jeden sos?
A) 28 B) 792 C) 29 D) 864
/Szkoła średnia
Wierzchołki 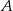 i
i 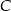 kwadratu
kwadratu 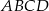 o polu 8 leżą na prostej o równaniu
o polu 8 leżą na prostej o równaniu 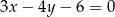 . Środek symetrii tego kwadratu ma współrzędne
. Środek symetrii tego kwadratu ma współrzędne 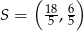 . Oblicz współrzędne punktów
. Oblicz współrzędne punktów  i
i  .
.
Promień kuli o polu powierzchni równym 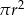 powiększono 2 razy. Objętość tak zmienionej kuli jest równa
powiększono 2 razy. Objętość tak zmienionej kuli jest równa
A) 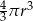 B)
B) 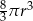 C)
C) 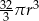 D)
D) 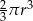
Promień kuli o polu powierzchni równym 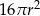 zmniejszono 2 razy. Objętość tak zmienionej kuli jest równa
zmniejszono 2 razy. Objętość tak zmienionej kuli jest równa
A) 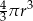 B)
B) 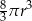 C)
C) 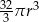 D)
D) 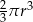
Promień kuli o polu powierzchni równym 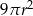 powiększono 2 razy. Objętość tak zmienionej kuli jest równa
powiększono 2 razy. Objętość tak zmienionej kuli jest równa
A) 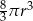 B)
B) 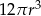 C)
C) 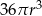 D)
D) 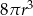
Dla jakich wartości parametru 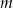 , równanie
, równanie 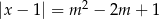 ma dwa pierwiastki dodatnie?
ma dwa pierwiastki dodatnie?
Wyznacz wszystkie wartości parametru  , dla których równanie
, dla których równanie 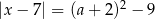 ma dwa różne rozwiązania dodatnie.
ma dwa różne rozwiązania dodatnie.
Wyznacz wszystkie wartości parametru  , dla których równanie
, dla których równanie 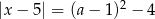 ma dwa różne rozwiązania dodatnie.
ma dwa różne rozwiązania dodatnie.
Dany jest nieskończony ciąg geometryczny 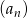 , w którym
, w którym 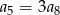 . Wtedy
. Wtedy
A) 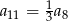 B)
B) 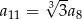 C)
C) 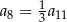 D)
D) 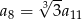
Dany jest nieskończony ciąg geometryczny 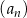 , w którym
, w którym 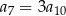 . Wtedy
. Wtedy
A) 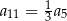 B)
B) 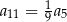 C)
C) 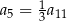 D)
D) 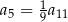
Wszystkie wyrazy nieskończonego ciągu geometrycznego 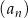 , określonego dla każdej liczby naturalnej
, określonego dla każdej liczby naturalnej 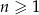 , są dodatnie i
, są dodatnie i 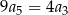 . Wtedy iloraz tego ciągu jest równy
. Wtedy iloraz tego ciągu jest równy
A)  B)
B)  C)
C) 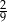 D)
D) 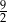
W dwóch pudełkach umieszczono po pięć kul, przy czym w pierwszym pudełku: 2 kule białe i 3 kule czerwone, a w drugim pudełku: 1 kulę białą i 4 kule czerwone. Z pierwszego pudełka losujemy jedną kulę i bez oglądania wkładamy ją do drugiego pudełka. Następnie losujemy jedną kulę z drugiego pudełka. Oblicz prawdopodobieństwo wylosowania kuli białej z drugiego pudełka.
W rozwinięciu wyrażenia 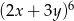 współczynnik przy iloczynie
współczynnik przy iloczynie 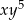 jest równy
jest równy
A) 1458 B) 2916 C) 972 D) 486
Granica jednostronna 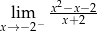
A) jest równa 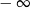 B) jest równa
B) jest równa 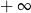 C) jest liczbą rzeczywistą D) nie istnieje
C) jest liczbą rzeczywistą D) nie istnieje
Granica jednostronna 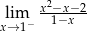
A) jest liczbą rzeczywistą B) jest równa 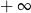 C) nie istnieje D) jest równa
C) nie istnieje D) jest równa 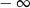
Granica jednostronna 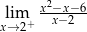
A) jest liczbą rzeczywistą B) jest równa 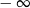 C) nie istnieje D) jest równa
C) nie istnieje D) jest równa 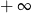
Granica jednostronna 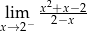
A) jest liczbą rzeczywistą B) jest równa 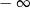 C) nie istnieje D) jest równa
C) nie istnieje D) jest równa 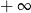
Granica jednostronna 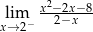
A) jest liczbą rzeczywistą B) nie istnieje C) jest równa 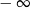 D) jest równa
D) jest równa 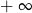
Granica jednostronna 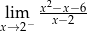
A) jest liczbą rzeczywistą B) jest równa 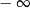 C) nie istnieje D) jest równa
C) nie istnieje D) jest równa 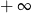
Granica jednostronna 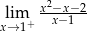
A) jest równa 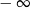 B) jest liczbą rzeczywistą C) nie istnieje D) jest równa
B) jest liczbą rzeczywistą C) nie istnieje D) jest równa 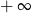
Granica jednostronna 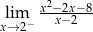
A) jest liczbą rzeczywistą B) jest równa 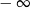 C) nie istnieje D) jest równa
C) nie istnieje D) jest równa 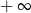
Granica jednostronna 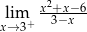
A) jest równa 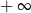 B) jest równa
B) jest równa 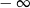 C) jest liczbą rzeczywistą D) nie istnieje
C) jest liczbą rzeczywistą D) nie istnieje
Granica jednostronna 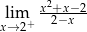
A) jest liczbą rzeczywistą B) jest równa 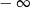 C) nie istnieje D) jest równa
C) nie istnieje D) jest równa 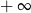
Granica jednostronna 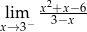
A) jest równa 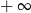 B) jest równa
B) jest równa 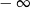 C) jest liczbą rzeczywistą D) nie istnieje
C) jest liczbą rzeczywistą D) nie istnieje
Granica jednostronna 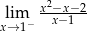
A) jest równa 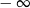 B) jest liczbą rzeczywistą C) nie istnieje D) jest równa
B) jest liczbą rzeczywistą C) nie istnieje D) jest równa 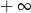
Granica jednostronna 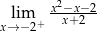
A) jest równa 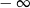 B) jest równa
B) jest równa 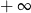 C) jest liczbą rzeczywistą D) nie istnieje
C) jest liczbą rzeczywistą D) nie istnieje
Granica jednostronna 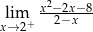
A) jest liczbą rzeczywistą B) nie istnieje C) jest równa 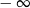 D) jest równa
D) jest równa 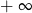
Granica jednostronna 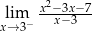
A) jest liczbą rzeczywistą B) jest równa 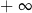 C) nie istnieje D) jest równa
C) nie istnieje D) jest równa 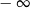
Granica jednostronna 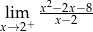
A) jest liczbą rzeczywistą B) jest równa 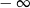 C) nie istnieje D) jest równa
C) nie istnieje D) jest równa 
Granica jednostronna 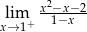
A) jest liczbą rzeczywistą B) jest równa 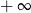 C) nie istnieje D) jest równa
C) nie istnieje D) jest równa 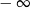
Rozwiąż nierówność  .
.
Stosunek pola powierzchni bocznej walca do pola przekroju osiowego tego walca
A) może być większy od 6 B) jest zawsze większy od 3
C) może być równy 3 D) jest zawsze mniejszy od 3
Listonosz losowo rozmieszcza 7 listów w 5 różnych skrzynkach na listy. Oblicz prawdopodobieństwo, że w każdej skrzynce znajdzie się przynajmniej jeden list.
Boki trójkąta 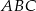 mają długości 12 cm, 15 cm, 18 cm. Trójkąt
mają długości 12 cm, 15 cm, 18 cm. Trójkąt 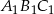 jest podobny do trójkąta
jest podobny do trójkąta 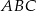 . Najdłuższy bok trójkąta
. Najdłuższy bok trójkąta 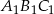 ma długość 6 cm. Obwód trójkąta
ma długość 6 cm. Obwód trójkąta 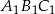 jest równy
jest równy
A) 15 cm B) 45 cm C) 22,5 cm D) 9 cm
Pewien graniastosłup ma 57 krawędzi. Liczba wszystkich ścian tego graniastosłupa jest równa
A) 19 B) 21 C) 38 D) 57
Ciąg 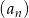 jest określony wzorem
jest określony wzorem 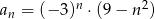 dla
dla 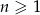 . Wynika stąd, że
. Wynika stąd, że
A) 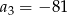 B)
B) 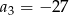 C)
C) 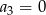 D)
D) 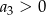
Ciąg 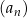 jest określony wzorem
jest określony wzorem 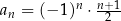 dla każdej liczby naturalnej
dla każdej liczby naturalnej 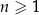 . Trzeci wyraz tego ciągu jest równy
. Trzeci wyraz tego ciągu jest równy
A) 2 B) 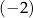 C) 3 D)
C) 3 D) 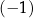
Ciąg 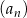 jest określony wzorem
jest określony wzorem 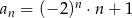 dla każdej liczby naturalnej
dla każdej liczby naturalnej 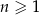 . Wtedy trzeci wyraz tego ciągu jest równy
. Wtedy trzeci wyraz tego ciągu jest równy
A) 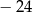 B)
B) 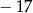 C)
C) 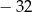 D)
D) 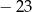
Ciąg 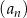 jest określony wzorem
jest określony wzorem 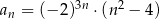 dla
dla 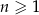 . Wówczas
. Wówczas
A) 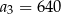 B)
B) 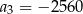 C)
C) 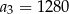 D)
D) 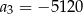
Ciąg 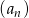 jest określony wzorem
jest określony wzorem 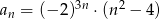 dla
dla 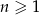 . Wówczas
. Wówczas
A) 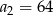 B)
B) 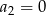 C)
C) 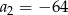 D)
D) 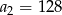
Dla 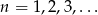 ciąg
ciąg 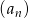 jest określony wzorem
jest określony wzorem 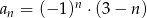 . Wtedy
. Wtedy
A) 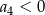 B)
B) 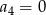 C)
C) 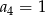 D)
D) 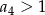
Ciąg 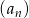 jest określony wzorem
jest określony wzorem 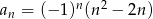 dla
dla 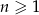 . Wtedy
. Wtedy
A) 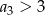 B)
B) 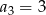 C)
C) 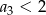 D)
D) 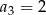
Dla 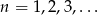 ciąg
ciąg 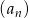 jest określony wzorem
jest określony wzorem 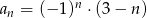 . Wtedy
. Wtedy
A) 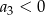 B)
B) 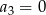 C)
C) 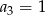 D)
D) 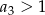
Ciąg 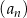 jest określony wzorem
jest określony wzorem 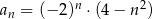 , dla
, dla 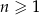 . Wtedy
. Wtedy
A) 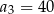 B)
B) 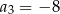 C)
C) 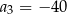 D)
D) 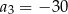
Wyznacz współrzędne punktu 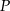 , który dzieli odcinek o końcach
, który dzieli odcinek o końcach 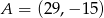 i
i 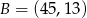 w stosunku
w stosunku 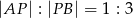 .
.
Wyznacz współrzędne punktu 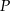 , który dzieli odcinek o końcach
, który dzieli odcinek o końcach 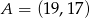 i
i 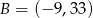 w stosunku
w stosunku 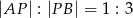 .
.
Rozwiąż równanie 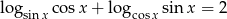 .
.
Gracz 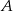 rzuca raz sześcienną kostką z liczbami 2,4 i 9 na ściankach, a gracz
rzuca raz sześcienną kostką z liczbami 2,4 i 9 na ściankach, a gracz 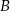 rzuca raz kostką z liczbami 3,5 i 7 przy czym każda liczba znajduje się na dwóch ściankach kostki. Wygrywa ten gracz, na którego kostce wypadnie większa liczba. Oblicz prawdopodobieństwo wygrania gracza
rzuca raz kostką z liczbami 3,5 i 7 przy czym każda liczba znajduje się na dwóch ściankach kostki. Wygrywa ten gracz, na którego kostce wypadnie większa liczba. Oblicz prawdopodobieństwo wygrania gracza 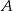 .
.
Rozwiąż równanie 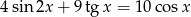 dla
dla 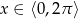 .
.
W kulę o promieniu długości 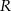 wpisano walec o największej objętości. Wyznacz stosunek objętości kuli do objętości tego walca.
wpisano walec o największej objętości. Wyznacz stosunek objętości kuli do objętości tego walca.
W kulę o promieniu długości 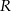 wpisano stożek o maksymalnej objętości. Oblicz objętość tego stożka.
wpisano stożek o maksymalnej objętości. Oblicz objętość tego stożka.
Nieskończony ciąg geometryczny 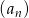 jest określony wzorem
jest określony wzorem 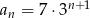 , dla
, dla 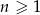 . Oblicz iloraz
. Oblicz iloraz 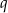 tego ciągu.
tego ciągu.
Nieskończony ciąg geometryczny 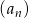 jest określony wzorem
jest określony wzorem 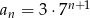 , dla
, dla 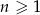 . Oblicz iloraz
. Oblicz iloraz 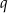 tego ciągu.
tego ciągu.
Nieskończony ciąg geometryczny 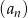 jest określony wzorem
jest określony wzorem 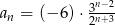 , dla
, dla 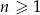 . Oblicz iloraz
. Oblicz iloraz 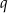 tego ciągu.
tego ciągu.

