Oblicz całkę 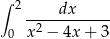 .
.
/Studia
Zbadaj monotoniczność ciągu określonego wzorem 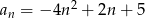 .
.
Zbadaj monotoniczność ciągu określonego wzorem 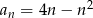 .
.
Zbadaj monotoniczność ciągu danego wzorem 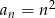 .
.
Zbadaj monotoniczność ciągu danego wzorem 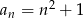 .
.
Wykaż, że jeżeli funkcje 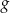 i
i 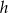 są określone w tym samym zbiorze i są rosnące, to funkcja określona wzorem
są określone w tym samym zbiorze i są rosnące, to funkcja określona wzorem 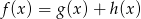 jest rosnąca.
jest rosnąca.
Korzystając ze wzoru 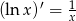 oblicz pochodną funkcji
oblicz pochodną funkcji 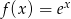 .
.
Napisz równanie stycznej do krzywej 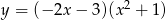 w punkcie
w punkcie 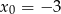 .
.
Oblicz granicę ciągu ![-----n+1----- nl→im+∞ n[ln(n+1)−lnn]](https://img.zadania.info/zad/1059240/HzadT0x.gif) .
.
Oblicz całkę niewłaściwą 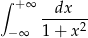 .
.
Oblicz całkę nieoznaczoną 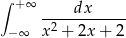 .
.
Zbadaj zbieżność całki niewłaściwej 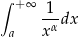 dla
dla 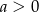 .
.
Oblicz całkę 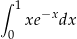 .
.
Wyznacz asymptoty funkcji 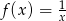 .
.
Oblicz całkę 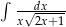 .
.
Oblicz całkę 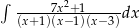 .
.
Oblicz pole obszaru ograniczonego parabolą 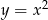 i prostą
i prostą 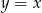 .
.
Oblicz pole obszaru ograniczonego parabolą 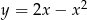 i prostą
i prostą 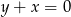 .
.
Oblicz całkę 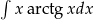 .
.
Oblicz całkę 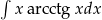 .
.
Zbadaj monotoniczność ciągu określonego wzorem 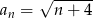 .
.
Oblicz granicę 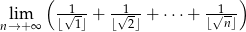 .
.
Uzasadnij, że nie istnieje granica 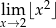 .
.
Uzasadnij, że nie istnieje granica 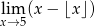 .
.
Napisz równanie stycznej do krzywej 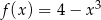 wiedząc, że jest ona równoległa do prostej
wiedząc, że jest ona równoległa do prostej 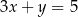 .
.
Funkcja 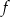 określona jest wzorem
określona jest wzorem 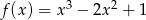 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania tych stycznych do wykresu funkcji
. Wyznacz równania tych stycznych do wykresu funkcji 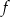 , które są równoległe do prostej o równaniu
, które są równoległe do prostej o równaniu 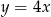 .
.
Funkcja 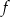 określona jest wzorem
określona jest wzorem 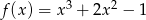 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania tych stycznych do wykresu funkcji
. Wyznacz równania tych stycznych do wykresu funkcji 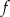 , które są równoległe do prostej o równaniu
, które są równoległe do prostej o równaniu 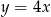 .
.
Oblicz całkę 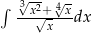 .
.
Wykazać, że jeśli równanie liniowe 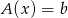 w
w 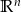 , ma dwa różne rozwiązania, to ma ich nieskończenie wiele.
, ma dwa różne rozwiązania, to ma ich nieskończenie wiele.

