Zadanie nr 1077727

Ciąg 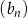(bn ) jest nieskończonym ciągiem liczb dodatnich, a ciąg 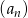(an) spełnia warunek

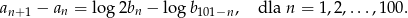
an+ 1 − an = lo g2bn − log b101−n, dla n = 1,2,...,100.

Oblicz 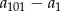a101 − a1 .

Wersja PDF

Rozwiązanie

Sposób I

Przekształćmy podany warunek

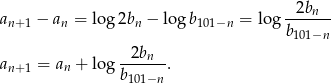
2b an+ 1 − an = log2bn − log b101−n = log ----n-- b101−n -2bn--- an+ 1 = an + log b . 101−n

Widać teraz, że mając jeden wyraz ciągu 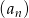(a ) n możemy obliczyć wszystkie jego wyrazy. Liczymy

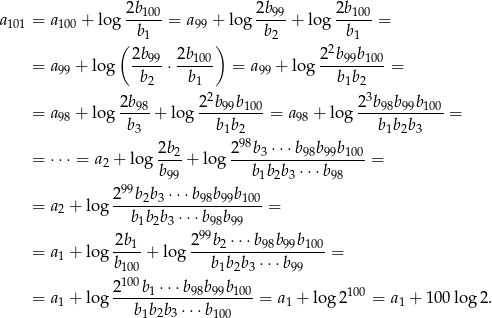
2b100 2b 99 2b100 a101 = a100 + lo g -----= a99 + log -----+ log ----- = ( b1 ) b2 b1 2b-99 2b100- 22b99b100 = a99 + log b ⋅ b = a99 + log b b = 2 1 1 2 2b98- 22b99b100- 23b98b99b100 = a98 + log b3 + lo g b1b2 = a98 + log b1b2b3 = 98 = ⋅⋅⋅ = a + log 2b2-+ log 2--b3⋅⋅-⋅b98b99b100-= 2 b99 b1b2b3⋅⋅⋅b 98 299b b ⋅⋅⋅ b b b = a2 + log ----2-3-----98--99-100-= b1b2b3 ⋅⋅⋅b98b99 2b1 2 99b2 ⋅⋅⋅b98b99b100 = a1 + log ----+ lo g-------------------= b100 b1b2b3 ⋅⋅⋅b99 2100b1⋅⋅⋅b98b99b100- 100 = a1 + log b1b2b3⋅⋅⋅b100 = a1 + log 2 = a1 + 100log 2.

Zatem

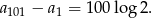
a101 − a1 = 10 0log 2.

Sposób II

Zapiszmy podany warunek w postaci

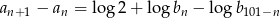
an+1 − an = log 2 + logbn − log b101−n

i wypiszmy pod sobą kolejne równości otrzymane przez podstawianie 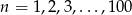n = 1,2,3,...,100 .

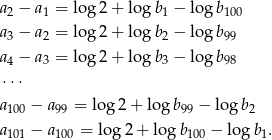
a − a = log 2 + logb − log b 2 1 1 100 a3 − a2 = log 2 + logb 2 − log b99 a − a = log 2 + logb − log b 4 3 3 98 ⋅⋅⋅ a100 − a99 = log 2+ log b99 − lo gb2 a101 − a100 = lo g2 + log b100 − log b1.

Dodając te równości stronami otrzymamy

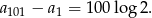
a101 − a1 = 10 0log 2.

Odpowiedź: 100 log 2