/Szkoła średnia/Zadania maturalne/Matura 2019
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 6 kwietnia 2019 Czas pracy: 170 minut
Zadania zamknięte
Do 2 kg roztworu soli dolano 0,25 litra wody i stężenie procentowe roztworu zmniejszyło się o 1 punkt procentowy. Jakie jest stężenie procentowe otrzymanego roztworu?
A) 8% B) 5% C) 9% D) 6%
Liczba 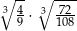 jest równa
jest równa
A)  B)
B) 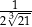 C)
C) 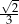 D)
D) 
Liczba 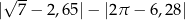 jest równa
jest równa
A) 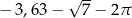 B)
B) 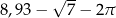 C)
C) 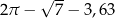 D)
D) 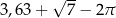
Liczba 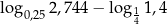 jest równa
jest równa
A) 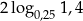 B)
B) 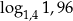 C)
C) 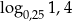 D) 0
D) 0
Na rysunku przedstawiony jest przedział 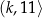 , gdzie
, gdzie 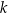 jest liczbą całkowitą. Suma wszystkich liczb całkowitych należących do tego przedziału jest równa
jest liczbą całkowitą. Suma wszystkich liczb całkowitych należących do tego przedziału jest równa 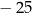 .
.

Stąd wynika, że
A) 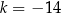 B)
B) 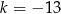 C)
C) 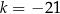 D)
D) 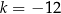
Funkcja kwadratowa określona jest wzorem 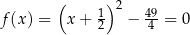 . Liczby
. Liczby 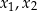 są różnymi miejscami zerowymi funkcji
są różnymi miejscami zerowymi funkcji 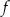 . Zatem
. Zatem
A) 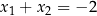 B)
B) 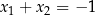 C)
C) 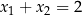 D)
D) 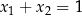
W tabeli podano dane dotyczące wyników z pracy klasowej z matematyki uzyskanych w pewnej klasie.
| Liczba uczniów | 2 | 4 | 7 | 2 | 3 | 2 |
| Ocena | 1 | 2 | 3 | 4 | 5 | 6 |
Różnica średniej arytmetycznej ocen i mediany wynosi
A) 0,3 B) 3,3 C) 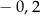 D) 3
D) 3
Na jednym z rysunków przedstawiono fragment wykresu funkcji kwadratowej określonej wzorem 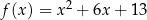 . Wskaż ten rysunek.
. Wskaż ten rysunek.
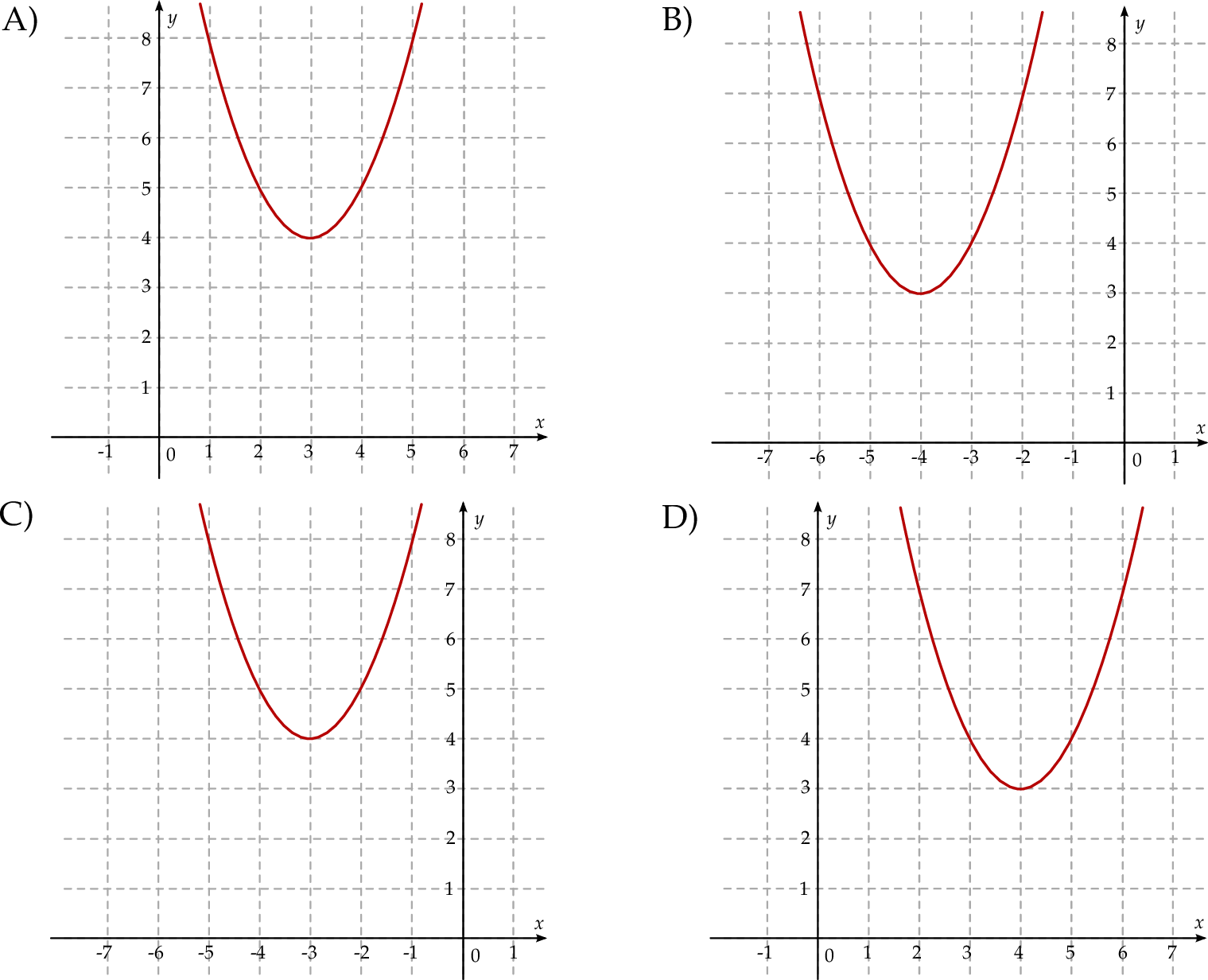
Liczba 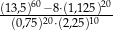 jest równa
jest równa
A) 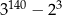 B)
B) 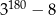 C)
C) 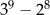 D)
D) 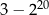
Wyrażenie 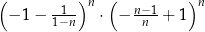 jest równe wyrażeniu
jest równe wyrażeniu
A) 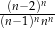 B)
B) 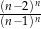 C)
C) 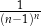 D)
D) 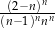
Liczba 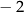 jest miejscem zerowym funkcji liniowej
jest miejscem zerowym funkcji liniowej 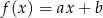 , a punkt
, a punkt 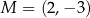 należy do wykresu tej funkcji. Współczynnik
należy do wykresu tej funkcji. Współczynnik  we wzorze tej funkcji jest równy
we wzorze tej funkcji jest równy
A) 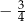 B)
B)  C)
C) 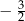 D)
D) 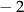
Punkt 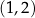 jest wierzchołkiem paraboli o równaniu
jest wierzchołkiem paraboli o równaniu
A) 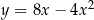 B)
B) 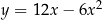 C)
C) 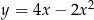 D)
D) 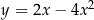
Punkty  i
i 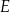 są środkami odpowiednio podstawy
są środkami odpowiednio podstawy 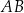 i ramienia
i ramienia 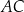 trójkąta równoramiennego
trójkąta równoramiennego 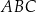 . Punkty
. Punkty 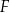 i
i 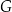 leżą na ramieniu
leżą na ramieniu 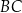 tak, że odcinki
tak, że odcinki 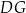 i
i 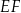 są prostopadłe do prostej
są prostopadłe do prostej 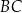 (zobacz rysunek).
(zobacz rysunek).
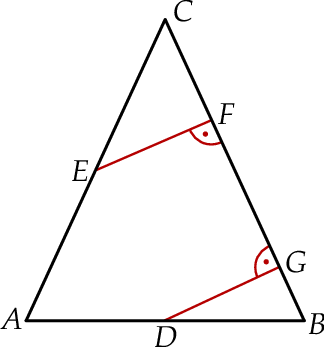
Pole trójkąta 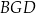 jest równe 2, a pole trójkąta
jest równe 2, a pole trójkąta 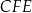 jest równe 4. Zatem pole trójkąta
jest równe 4. Zatem pole trójkąta 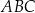 jest równe
jest równe
A) 24 B) 8 C) 12 D) 16
Dany jest ciąg arytmetyczny 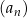 określony wzorem
określony wzorem 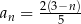 dla każdej liczby całkowitej
dla każdej liczby całkowitej 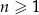 . Różnica
. Różnica  tego ciągu jest równa
tego ciągu jest równa
A) 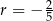 B)
B) 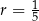 C)
C) 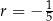 D)
D) 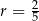
Podstawy trapezu równoramiennego 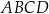 mają długości 8 i 16, a przekątne tego trapezu mają długość 15 (zobacz rysunek).
mają długości 8 i 16, a przekątne tego trapezu mają długość 15 (zobacz rysunek).
Wtedy miara  kąta ostrego
kąta ostrego  tego trójkąta spełnia warunek
tego trójkąta spełnia warunek
A) 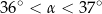 B)
B) 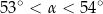 C)
C) 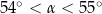 D)
D) 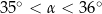
Dla pewnej liczby  ciąg
ciąg 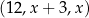 jest geometryczny. Liczba
jest geometryczny. Liczba  jest równa
jest równa
A) 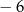 B) 9 C) 6 D) 3
B) 9 C) 6 D) 3
Na trójkącie 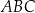 opisano okrąg i poprowadzono styczną do okręgu w punkcie
opisano okrąg i poprowadzono styczną do okręgu w punkcie 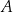 (zobacz rysunek obok).
(zobacz rysunek obok).
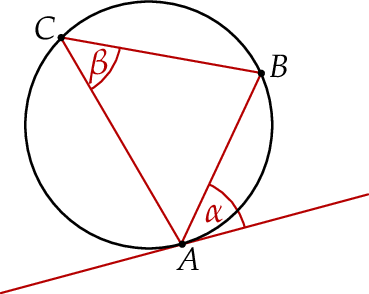
Jeżeli 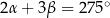 , to
, to
A) 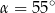 B)
B) 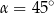 C)
C) 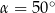 D)
D) 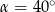
Punkt 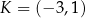 jest wierzchołkiem trójkąta równoramiennego
jest wierzchołkiem trójkąta równoramiennego 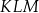 , w którym
, w którym 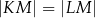 . Odcinek
. Odcinek 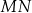 jest wysokością trójkąta i
jest wysokością trójkąta i 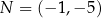 . Zatem
. Zatem
A) 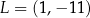 B)
B) 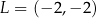 C)
C) 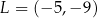 D)
D) 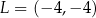
Wartość wyrażenia 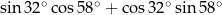 jest równa
jest równa
A) 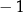 B) 1 C) 0 D) 2
B) 1 C) 0 D) 2
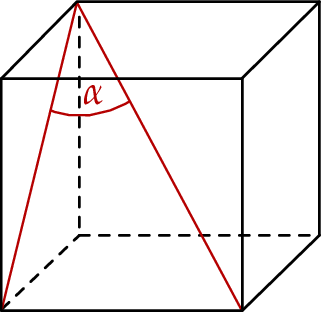
Jeżeli  oznacza miarę kąta między przekątną sześcianu a przekątną ściany bocznej tego sześcianu (zobacz rysunek), to
oznacza miarę kąta między przekątną sześcianu a przekątną ściany bocznej tego sześcianu (zobacz rysunek), to
A) 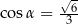 B)
B) 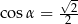 C)
C) 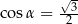 D)
D) 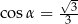
Na rysunku przedstawiono bryłę zbudowaną z walca, stożka i półkuli. Wysokość walca jest równa  i jest taka sama jak wysokość stożka, oraz taka sama jak promień półkuli, promień podstawy walca i promień podstawy stożka.
i jest taka sama jak wysokość stożka, oraz taka sama jak promień półkuli, promień podstawy walca i promień podstawy stożka.
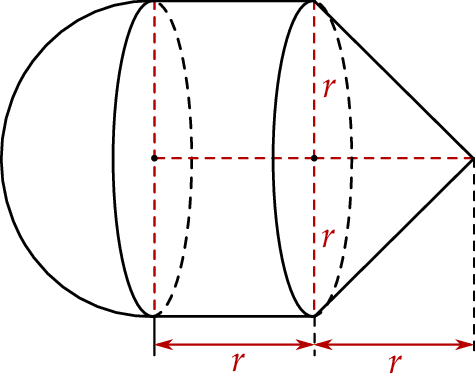
Objętość tej bryły jest równa
A) 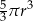 B)
B) 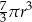 C)
C) 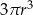 D)
D) 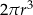
Gdy dodamy liczbę wszystkich krawędzi pewnego graniastosłupa do liczby wszystkich jego wierzchołków, to otrzymamy w wyniku 25. Liczba wszystkich krawędzi tego graniastosłupa jest równa
A) 9 B) 5 C) 6 D) 15
Liczba wszystkich dodatnich liczb pięciocyfrowych, które są podzielne przez 3, i których cyfry należą do zbioru 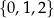 , jest równa
, jest równa
A) 81 B) 54 C) 162 D) 243
Pewnego dnia w klasie Ib było dwa razy więcej uczniów, niż w klasie Ia. Tego samego dnia dziewczynki stanowiły 60% uczniów klasy Ia, oraz 40% uczniów klasy Ib. Jeżeli tego dnia wylosujemy jednego ucznia z klas Ia i Ib, to prawdopodobieństwo wylosowania chłopca jest równe
A) 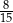 B)
B) 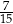 C)
C) 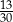 D)
D) 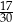
Zadania otwarte
Rozwiąż nierówność 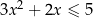 .
.
Wykaż, że reszta z dzielenia sumy kwadratów czterech kolejnych nieparzystych liczb naturalnych przez 16 jest równa 4.
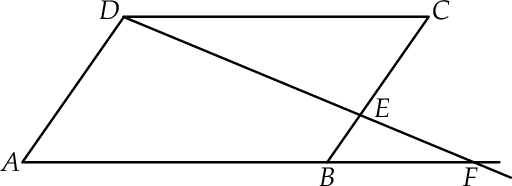
W równoległoboku 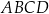 punkt
punkt 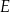 jest takim punktem boku
jest takim punktem boku 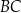 , że
, że 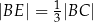 . Z wierzchołka
. Z wierzchołka 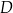 poprowadzono prostą przecinającą bok
poprowadzono prostą przecinającą bok 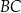 w punkcie
w punkcie 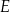 . Proste
. Proste 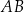 i
i 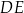 przecinają się w punkcie
przecinają się w punkcie 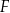 (zobacz rysunek). Wykaż, że pole trójkąta
(zobacz rysunek). Wykaż, że pole trójkąta 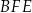 stanowi
stanowi 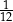 pola równoległoboku
pola równoległoboku  .
.
Uzasadnij, że rozwinięcie dziesiętne liczby 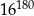 ma więcej niż 216 cyfr.
ma więcej niż 216 cyfr.
Prosta 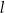 przecina okrąg o środku
przecina okrąg o środku 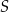 w punktach
w punktach 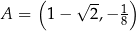 i
i 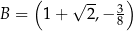 . Punkt
. Punkt 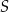 leży na prostej
leży na prostej 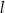 . Oblicz pole koła ograniczonego tym okręgiem.
. Oblicz pole koła ograniczonego tym okręgiem.
Wykres funkcji wykładniczej 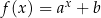 (gdzie
(gdzie 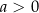 i
i 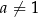 ) przesunięto o 4 jednostki w prawo i 2 jednostki w dół. W rezultacie otrzymano wykres funkcji
) przesunięto o 4 jednostki w prawo i 2 jednostki w dół. W rezultacie otrzymano wykres funkcji 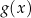 , który przecina oś
, który przecina oś 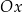 w punkcie
w punkcie 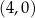 oraz przechodzi przez punkt
oraz przechodzi przez punkt 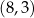 . Wyznacz
. Wyznacz  i
i 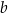 oraz rozwiąż nierówność
oraz rozwiąż nierówność 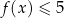 .
.
Ze zbioru 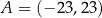 losujemy dwucyfrową liczbę całkowitą
losujemy dwucyfrową liczbę całkowitą  , natomiast ze zbioru
, natomiast ze zbioru 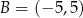 losujemy liczbę całkowitą
losujemy liczbę całkowitą 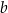 . Te liczby są współczynnikami funkcji
. Te liczby są współczynnikami funkcji 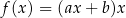 . Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wykres otrzymanej funkcji
. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wykres otrzymanej funkcji  ma co najmniej dwa punkty wspólne z prostą
ma co najmniej dwa punkty wspólne z prostą 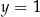 .
.
Dany jest ciąg arytmetyczny 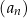 określony dla każdej liczby naturalnej
określony dla każdej liczby naturalnej 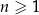 , w którym suma pierwszych 60 wyrazów jest równa 108 750, a suma wyrazów o numerach od 31 do 50 (włącznie) jest równa 34 850. Wyznacz największy wyraz tego ciągu.
, w którym suma pierwszych 60 wyrazów jest równa 108 750, a suma wyrazów o numerach od 31 do 50 (włącznie) jest równa 34 850. Wyznacz największy wyraz tego ciągu.
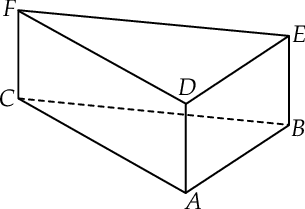
Dany jest graniastosłup prawidłowy trójkątny (zobacz rysunek). Objętość tego graniastosłupa jest równa 324. Pole podstawy graniastosłupa jest równe polu jednej ściany bocznej. Oblicz pole powierzchni całkowitej tego graniastosłupa.