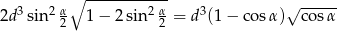/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Prawidłowy czworokątny

Zadanie nr 5319705

Dodaj do ulubionych
Dodaj do rozwiązanych

W graniastosłupie prawidłowym czworokątnym przekątne ścian bocznych, wychodzące z tego samego wierzchołka, mają długość 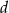d i tworzą kąt o mierze α . Oblicz objętość tego graniastosłupa.

Rozwiązanie

Rozpoczynamy od rysunku.

PIC

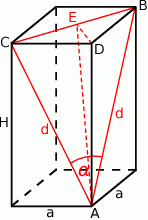
Oznaczmy długość krawędzi podstawy graniastosłupa przez a , a długość jego wysokości przez 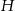H . Ponadto niech 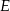E będzie środkiem przekątnej BC .

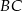Sposób I

Trójkąt 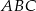ABC jest równoramienny, więc odcinek 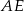AE jest jego wysokością, a jednocześnie dwusieczną kąta 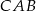CAB . Z trójkąta prostokątnego 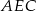AEC możemy obliczyć a w zależności od α i d .

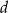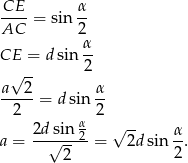
CE-- α- AC = sin 2 α CE = d sin-- √ -- 2 a--2- α- 2 = d sin 2 2dsin α √ -- α a = --√---2-= 2dsin -. 2 2

Długość wysokości możemy wyliczyć np. z trójkąta prostokątnego 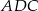ADC

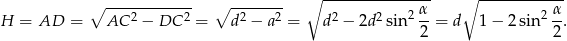
∘ --------------- ∘ ------------ ∘ ----2------2 ∘ --2---2- 2 2 2 α- 2 α H = AD = AC − DC = d − a = d − 2d sin 2 = d 1 − 2 sin 2 .

Pozostało obliczyć objętość ostrosłupa.

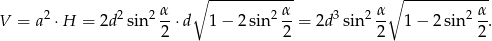
∘ ------------ ∘ ------------ 2 2 2 α 2 α- 3 2 α- 2 α- V = a ⋅H = 2d sin 2 ⋅d 1− 2sin 2 = 2d sin 2 1− 2sin 2.

Sposób II

Tym razem skorzystamy z twierdzenia cosinusów w trójkącie 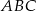ABC .

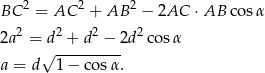
BC 2 = AC 2 + AB 2 − 2AC ⋅AB cos α 2 2 2 2 2a = d + d − 2d cosα √ --------- a = d 1 − co sα.

Długość wysokości 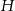H graniastosłupa obliczamy podobnie jak w poprzednim sposobie – korzystamy z twierdzenia Pitagorasa w trójkącie ADC .

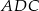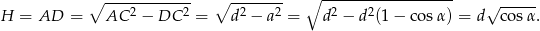
∘ ------------ ∘ -------- ∘ ------------------ √ ----- H = AD = AC 2 − DC 2 = d2 − a2 = d2 − d2(1 − cos α) = d co sα.

Liczymy objętość

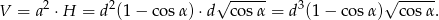
2 2 √ ----- 3 √ ----- V = a ⋅ H = d (1− cosα )⋅d cosα = d (1− cosα ) cosα.

 
Odpowiedź: ∘ ------------ 3 2 α 2 α 3 √ ----- 2d sin 2 1− 2sin 2 = d (1 − cos α) cos α

Wersja PDF