W trójkącie 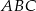 , gdzie
, gdzie 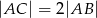 dane są
dane są 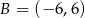 i
i 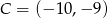 . Wyznacz współrzędne wierzchołka
. Wyznacz współrzędne wierzchołka 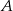 , jeżeli leży on na prostej
, jeżeli leży on na prostej 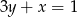 .
.
/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt
Punkty 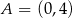 i
i 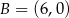 są końcami odcinka
są końcami odcinka 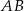 . Prosta
. Prosta 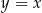 przecina odcinek
przecina odcinek 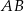 w punkcie
w punkcie 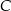 . Oblicz stosunek
. Oblicz stosunek 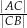 .
.
Punkty 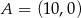 i
i 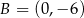 są końcami odcinka
są końcami odcinka 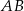 . Prosta
. Prosta 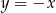 przecina odcinek
przecina odcinek 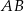 w punkcie
w punkcie 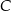 . Oblicz stosunek
. Oblicz stosunek 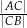 .
.
Prosta o równaniu 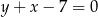 zawiera jedną z dwusiecznych kątów wewnętrznych trójkąta
zawiera jedną z dwusiecznych kątów wewnętrznych trójkąta 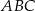 , w którym
, w którym 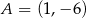 i
i 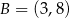 . Oblicz pole tego trójkąta.
. Oblicz pole tego trójkąta.
Punkty 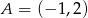 i
i 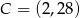 są wierzchołkami trójkąta równoramiennego, w którym
są wierzchołkami trójkąta równoramiennego, w którym 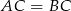 . Prosta zawierająca wysokość opuszczoną z wierzchołka
. Prosta zawierająca wysokość opuszczoną z wierzchołka 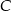 ma równanie
ma równanie 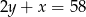 . Oblicz pole trójkąta
. Oblicz pole trójkąta 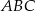 .
.
Wierzchołkami kwadratu 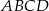 są punkty o współrzędnych
są punkty o współrzędnych 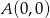 ,
, 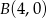 ,
, 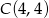 i
i 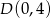 . Dla każdej liczby rzczywistej
. Dla każdej liczby rzczywistej 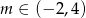 rozważamy trójkąt o wierzchołkach
rozważamy trójkąt o wierzchołkach 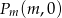 ,
, 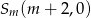 i
i 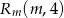 . Wyznacz wszystkie wartości prametru
. Wyznacz wszystkie wartości prametru 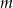 , dla których pole figury, która jest częścią wspólną kwadratu
, dla których pole figury, która jest częścią wspólną kwadratu 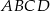 i trójkąta
i trójkąta 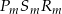 wynosi 2.
wynosi 2.
Wyznacz równanie takiej prostej przechodzącej przez punkt 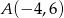 , która wraz z osiami układu współrzędnych ogranicza trójkąt o polu równym 2.
, która wraz z osiami układu współrzędnych ogranicza trójkąt o polu równym 2.
W okrąg o równaniu 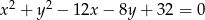 wpisano trójkąt równoboczny
wpisano trójkąt równoboczny 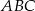 w którym
w którym 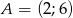 . Oblicz współrzędne pozostałych wierzchołków trójkąta.
. Oblicz współrzędne pozostałych wierzchołków trójkąta.
Napisz równanie symetralnej boku 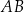 trójkąta
trójkąta 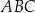 o wierzchołkach
o wierzchołkach 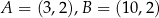 i
i 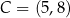 .
.
Dane są proste o równaniach 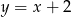 oraz
oraz 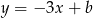 , które przecinają się w punkcie leżącym na osi
, które przecinają się w punkcie leżącym na osi 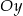 układu współrzędnych. Oblicz pole trójkąta, którego dwa boki zawierają się w danych prostych, a trzeci jest zawarty w osi
układu współrzędnych. Oblicz pole trójkąta, którego dwa boki zawierają się w danych prostych, a trzeci jest zawarty w osi 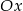 .
.
Dane są proste o równaniach 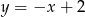 oraz
oraz 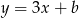 , które przecinają się w punkcie leżącym na osi
, które przecinają się w punkcie leżącym na osi 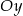 układu współrzędnych. Oblicz pole trójkąta, którego dwa boki zawierają się w danych prostych, a trzeci jest zawarty w osi
układu współrzędnych. Oblicz pole trójkąta, którego dwa boki zawierają się w danych prostych, a trzeci jest zawarty w osi 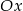 .
.
Dane są proste o równaniach 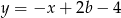 oraz
oraz 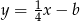 , które przecinają się w punkcie leżącym na osi
, które przecinają się w punkcie leżącym na osi 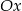 układu współrzędnych. Oblicz pole trójkąta, którego dwa boki zawierają się w danych prostych, a trzeci jest zawarty w osi
układu współrzędnych. Oblicz pole trójkąta, którego dwa boki zawierają się w danych prostych, a trzeci jest zawarty w osi 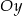 .
.
Oblicz pole trójkąta 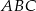 , którego boki zawierają się w prostych o równaniach:
, którego boki zawierają się w prostych o równaniach: 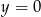 ,
, 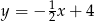 oraz
oraz 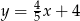 .
.
Oblicz pole trójkąta 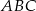 , którego boki zawierają się w prostych o równaniach:
, którego boki zawierają się w prostych o równaniach: 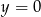 ,
, 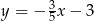 oraz
oraz 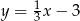 .
.
Podstawa 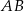 trójkąta równoramiennego
trójkąta równoramiennego 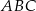 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 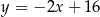 . Wierzchołki
. Wierzchołki 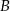 i
i 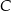 mają współrzędne
mają współrzędne 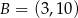 i
i 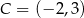 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 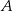 i pole trójkąta
i pole trójkąta 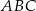 .
.
Podstawa 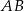 trójkąta równoramiennego
trójkąta równoramiennego 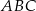 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 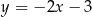 . Wierzchołki
. Wierzchołki 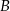 i
i 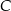 mają współrzędne
mają współrzędne 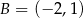 i
i 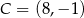 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 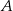 i pole trójkąta
i pole trójkąta 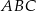 .
.
Punkt 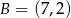 jest wierzchołkiem trójkąta równoramiennego
jest wierzchołkiem trójkąta równoramiennego 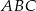 o podstawie
o podstawie 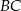 . Pole tego trójkąta jest równe 20, a wysokość poprowadzona z wierzchołka
. Pole tego trójkąta jest równe 20, a wysokość poprowadzona z wierzchołka 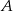 tego trójkąta zawiera się w prostej o równaniu
tego trójkąta zawiera się w prostej o równaniu 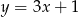 . Oblicz współrzędne punktów
. Oblicz współrzędne punktów 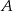 i
i 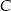 . Rozważ wszystkie przypadki.
. Rozważ wszystkie przypadki.
Pole trójkąta 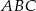 o danych wierzchołkach
o danych wierzchołkach 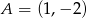 oraz
oraz 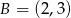 jest równe 4,5. Wyznacz współrzędne trzeciego wierzchołka wiedząc, że należy on do prostej o równaniu
jest równe 4,5. Wyznacz współrzędne trzeciego wierzchołka wiedząc, że należy on do prostej o równaniu 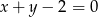 .
.
Dane są punkty 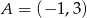 i
i 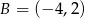 . Wyznacz współrzędne punktu
. Wyznacz współrzędne punktu 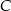 na prostej
na prostej 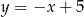 tak, aby pole trójkąta
tak, aby pole trójkąta 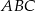 było równe 7.
było równe 7.
Znajdź taki punkt 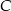 , leżący na prostej
, leżący na prostej 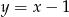 , aby pole trójkąta
, aby pole trójkąta 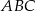 , którego wierzchołkami są punkty:
, którego wierzchołkami są punkty: 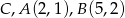 było równe 5.
było równe 5.
Dane są punkty 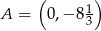 i
i 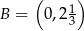 . Wyznacz na prostej
. Wyznacz na prostej 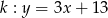 punkt
punkt 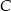 , tak aby
, tak aby 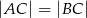 . Dla wyznaczonego punktu C:
. Dla wyznaczonego punktu C:
- wykaż, że trójkąt
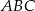 jest prostokątny;
jest prostokątny; - wyznacz równanie okręgu opisanego na trójkącie
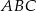 .
.
Punkty 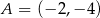 i
i 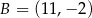 są wierzchołkami trójkąta
są wierzchołkami trójkąta 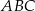 . Wierzchołek
. Wierzchołek 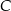 tego trójkąta leży na prostej
tego trójkąta leży na prostej 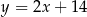 , a dwusieczna kąta
, a dwusieczna kąta 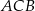 przecina bok
przecina bok 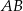 w punkcie
w punkcie 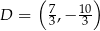 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 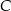 trójkąta
trójkąta 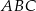 .
.
Oblicz pole i obwód trójkąta o wierzchołkach: 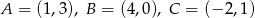 .
.
Okrąg wpisany w trójkąt 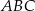 jest opisany równaniem
jest opisany równaniem
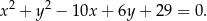
Punkty styczności tego okręgu z bokami 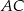 i
i 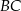 trójkąta
trójkąta 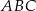 leżą na prostej o równaniu:
leżą na prostej o równaniu: 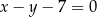 . Wyznacz współrzędne wierzchołka
. Wyznacz współrzędne wierzchołka 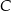 trójkąta
trójkąta 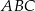 .
.
Boki 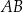 i
i 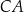 trójkąta
trójkąta 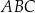 są zawarte w prostych
są zawarte w prostych 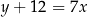 i
i 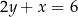 , a jego dwa wierzchołki mają współrzędne
, a jego dwa wierzchołki mają współrzędne 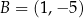 i
i 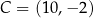 . Oblicz pole tego trójkąta.
. Oblicz pole tego trójkąta.
W trójkącie 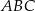 o polu 20 dane sa współrzędne dwóch wierzchołków:
o polu 20 dane sa współrzędne dwóch wierzchołków:  ,
, 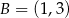 oraz środek
oraz środek 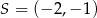 okręgu opisanego na tym trójkącie. Wyznacz współrzędne wierzchołka
okręgu opisanego na tym trójkącie. Wyznacz współrzędne wierzchołka 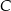 .
.
Dane są punkty 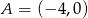 i
i 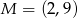 oraz prosta
oraz prosta 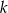 o równaniu
o równaniu 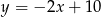 . Wierzchołek
. Wierzchołek 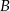 trójkąta
trójkąta 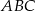 to punkt przecięcia prostej
to punkt przecięcia prostej 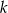 z osią
z osią 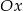 układu współrzędnych, a wierzchołek
układu współrzędnych, a wierzchołek 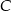 jest punktem przecięcia prostej
jest punktem przecięcia prostej 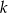 z prostą
z prostą 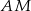 . Oblicz pole trójkąta
. Oblicz pole trójkąta 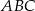 .
.
Dane są punkty 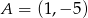 i
i 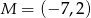 oraz prosta
oraz prosta 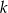 o równaniu
o równaniu 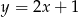 . Wierzchołek
. Wierzchołek 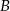 trójkąta
trójkąta 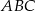 to punkt przecięcia prostej
to punkt przecięcia prostej 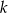 z prostą
z prostą 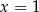 , a wierzchołek
, a wierzchołek 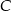 jest punktem przecięcia prostej
jest punktem przecięcia prostej 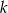 z prostą
z prostą 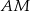 . Oblicz pole trójkąta
. Oblicz pole trójkąta 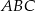 .
.
Dany jest wierzchołek trójkąta równobocznego 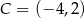 . Bok
. Bok 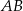 zawarty jest w prostej o równaniu
zawarty jest w prostej o równaniu 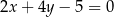 . Wyznacz długość boku tego trójkąta.
. Wyznacz długość boku tego trójkąta.

