Dziewiąty wyraz ciągu arytmetycznego 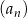 , określonego dla
, określonego dla 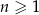 , jest równy 34, a suma jego ośmiu początkowych wyrazów jest równa 110. Oblicz pierwszy wyraz i różnicę tego ciągu.
, jest równy 34, a suma jego ośmiu początkowych wyrazów jest równa 110. Oblicz pierwszy wyraz i różnicę tego ciągu.
/Szkoła średnia/Ciągi/Arytmetyczny
Jedenasty wyraz ciągu arytmetycznego 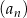 , określonego dla
, określonego dla 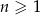 , jest równy
, jest równy 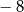 , a suma jego dziesięciu początkowych wyrazów jest równa
, a suma jego dziesięciu początkowych wyrazów jest równa 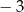 . Oblicz pierwszy wyraz i różnicę tego ciągu.
. Oblicz pierwszy wyraz i różnicę tego ciągu.
Suma ośmiu początkowych wyrazów ciągu arytmetycznego 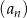 , określonego dla
, określonego dla 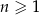 , jest równa 90, a suma
, jest równa 90, a suma 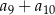 jest równa 57,5. Oblicz pierwszy wyraz i różnicę tego ciągu.
jest równa 57,5. Oblicz pierwszy wyraz i różnicę tego ciągu.
Pięćdziesiąty wyraz ciągu arytmetycznego 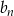 jest równy 5. Oblicz
jest równy 5. Oblicz 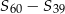 , gdzie
, gdzie 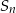 oznacza sumę
oznacza sumę  początkowych wyrazów ciągu
początkowych wyrazów ciągu 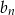 .
.
Ciąg 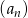 , gdzie
, gdzie 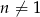 jest ciągiem arytmetycznym w którym
jest ciągiem arytmetycznym w którym 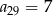 . Oblicz
. Oblicz 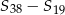 , gdzie
, gdzie 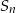 oznacza sumę
oznacza sumę  początkowych wyrazów ciągu
początkowych wyrazów ciągu 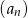 .
.
Jednym z pierwiastków trójmianu kwadratowego 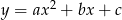 jest
jest 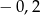 . Liczby
. Liczby 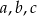 tworzą w podanej kolejności ciąg arytmetyczny, a ich suma wynosi 24. Oblicz drugi pierwiastek tego trójmianu.
tworzą w podanej kolejności ciąg arytmetyczny, a ich suma wynosi 24. Oblicz drugi pierwiastek tego trójmianu.
Jedno z rozwiązań równania 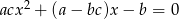 z niewiadomą
z niewiadomą  jest równe 4. Liczby
jest równe 4. Liczby 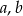 i
i  (w podanej kolejności) tworzą ciąg arytmetyczny, w którym pierwszy wyraz jest o 6 większy od trzeciego. Znajdź drugie rozwiązanie tego równania.
(w podanej kolejności) tworzą ciąg arytmetyczny, w którym pierwszy wyraz jest o 6 większy od trzeciego. Znajdź drugie rozwiązanie tego równania.
W ciągu arytmetycznym 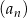 , określonym dla
, określonym dla 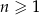 , dane są wyrazy:
, dane są wyrazy: 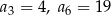 . Wyznacz wszystkie wartości
. Wyznacz wszystkie wartości  , dla których wyrazy ciągu
, dla których wyrazy ciągu 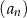 są mniejsze od 200.
są mniejsze od 200.
W ciągu arytmetycznym 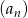 dane są wyrazy:
dane są wyrazy: 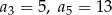 . Oblicz, ile wyrazów ciągu
. Oblicz, ile wyrazów ciągu 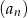 jest mniejszych niż 83.
jest mniejszych niż 83.
Wykaż, że jeżeli liczby 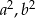 i
i 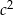 tworzą ciąg arytmetyczny, który nie jest stały, to liczby
tworzą ciąg arytmetyczny, który nie jest stały, to liczby 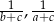 i
i 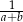 również tworzą ciąg arytmetyczny.
również tworzą ciąg arytmetyczny.
Liczby 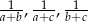 , gdzie
, gdzie 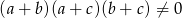 są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że liczby
są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że liczby 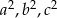 są również wyrazami ciągu arytmetycznego.
są również wyrazami ciągu arytmetycznego.
Nieskończony ciąg liczbowy 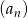 dla
dla 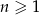 jest określony wzorem
jest określony wzorem
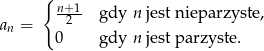
- Uzupełnij tabelkę:

1 2 3 4 5 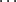
2005 2006 2007 2008 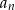
1 0 … - Oblicz
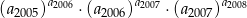 .
. - Oblicz sumę 2008 początkowych wyrazów ciągu
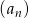 .
.
W ciągu arytmetycznym o nieparzystej liczbie wyrazów suma wyrazów stojących na miejscach nieparzystych równa się 44, a suma pozostałych wynosi 33. Znajdź wyraz środkowy i liczbę wyrazów tego ciągu.
Na płaszczyźnie z prostokątnym układem współrzędnych zilustruj zbiór wszystkich punktów płaszczyzny o współrzędnych 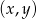 , dla których ciąg:
, dla których ciąg: 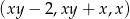 jest rosnącym ciągiem arytmetycznym.
jest rosnącym ciągiem arytmetycznym.
Pierwszy wyraz ciągu arytmetycznego jest równy 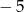 , a suma dwudziestu początkowych wyrazów tego ciągu jest równa 1230. Wyznacz różnicę tego ciągu.
, a suma dwudziestu początkowych wyrazów tego ciągu jest równa 1230. Wyznacz różnicę tego ciągu.
Długości boków prostokąta i długość jego przekątnej tworzą ciąg arytmetyczny. Oblicz długości jego boków, jeśli obwód prostokąta jest równy 14.
Długości boków prostokąta i długość jego przekątnej tworzą ciąg arytmetyczny. Oblicz długości jego boków, jeśli pole prostokąta jest równe 48.
Oblicz wyrazy 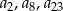 ciągu arytmetycznego jeśli
ciągu arytmetycznego jeśli 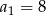 i
i 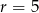 .
.
Pierwszy wyraz malejącego ciągu arytmetycznego 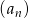 jest równy 3, a iloczyn wyrazów czwartego i piątego równy jest 15. Oblicz różnicę ciągu
jest równy 3, a iloczyn wyrazów czwartego i piątego równy jest 15. Oblicz różnicę ciągu 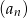 oraz sumę 14 jego początkowych wyrazów.
oraz sumę 14 jego początkowych wyrazów.
W ciągu arytmetycznym 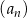 , określonym dla
, określonym dla 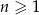 , suma 221 początkowych wyrazów jest równa 1547. Oblicz sumę
, suma 221 początkowych wyrazów jest równa 1547. Oblicz sumę 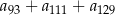 .
.
Suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 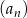 dla każdego
dla każdego 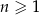 określona jest wzorem
określona jest wzorem 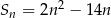 .
.
- Wykaż, że ciąg
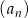 jest ciągiem arytmetycznym.
jest ciągiem arytmetycznym. - Wykaż, że jeżeli suma
 początkowych wyrazów ciągu dla każdego
początkowych wyrazów ciągu dla każdego 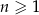 określona jest wzorem
określona jest wzorem 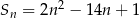 , to ciąg ten nie jest arytmetyczny.
, to ciąg ten nie jest arytmetyczny. - Znajdź takie trzy kolejne wyrazy ciągu
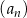 , aby kwadrat środkowego wyrazu był o 48 mniejszy od różnicy kwadratów wyrazów z nim sąsiadujących.
, aby kwadrat środkowego wyrazu był o 48 mniejszy od różnicy kwadratów wyrazów z nim sąsiadujących.
Suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 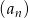 wyraża się wzorem
wyraża się wzorem 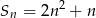 dla
dla 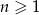 . Oblicz pierwszy wyraz ciągu i jego różnice.
. Oblicz pierwszy wyraz ciągu i jego różnice.
Suma 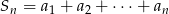 początkowych
początkowych  wyrazów pewnego ciągu arytmetycznego
wyrazów pewnego ciągu arytmetycznego 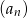 jest określona wzorem
jest określona wzorem 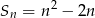 dla
dla 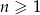 . Wyznacz wzór na
. Wyznacz wzór na  -ty wyraz tego ciągu.
-ty wyraz tego ciągu.
Suma 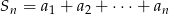 początkowych
początkowych  wyrazów pewnego ciągu arytmetycznego
wyrazów pewnego ciągu arytmetycznego 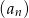 jest określona wzorem
jest określona wzorem 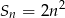 dla
dla 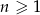 . Wyznacz wzór na
. Wyznacz wzór na  -ty wyraz tego ciągu.
-ty wyraz tego ciągu.
Pierwszy wyraz ciągu arytmetycznego 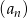 jest równy
jest równy 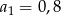 , a jego różnica jest równa
, a jego różnica jest równa 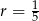 . Oblicz
. Oblicz 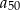 oraz sumę 50 początkowych wyrazów ciągu
oraz sumę 50 początkowych wyrazów ciągu 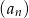 .
.
W trójkącie dwa boki mają długość 3 cm i 4 cm. Długość trzeciego boku jest większa od długości dwóch pozostałych boków. Długości wysokości w tym trójkącie są trzema kolejnymi wyrazami ciągu arytmetycznego. Oblicz pole tego trójkąta oraz długości promieni okręgów: wpisanego w ten trójkąt i opisanego na tym trójkącie.
Sześcian największej z czterech różnych liczb całkowitych, tworzących rosnący ciąg arytmetyczny o wyrazach dodatnich, jest równy sumie sześcianów pozostałych liczb. Wykaż, że iloczyn dwóch z tych liczb jest o 60% większy od iloczynu dwóch pozostałych.
Ile liczb trzeba wstawić między liczby 62 i 440, aby otrzymać ciąg arytmetyczny, którego suma jest równa 2008? Wyznacz różnicę tego ciągu.
Ile liczb trzeba wstawić między liczby 16 i 250, aby otrzymać ciąg arytmetyczny, którego suma jest równa 1995? Wyznacz różnicę tego ciągu.

