/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 25 lutego 2017 Czas pracy: 180 minut
Zadania zamknięte
Liczba 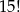 jest podzielna przez
jest podzielna przez
A) 91 B) 71 C) 51 D) 41
Liczba 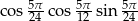 jest równa
jest równa
A) 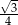 B)
B) 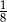 C)
C) 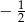 D)
D) 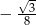
Granica 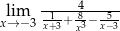
A) jest równa 0 B) jest równa 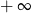 C) jest równa
C) jest równa 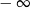 D) nie istnieje
D) nie istnieje
Funkcja 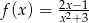 jest określona dla każdej liczby rzeczywistej
jest określona dla każdej liczby rzeczywistej  . Pochodna tej funkcji jest określona wzorem
. Pochodna tej funkcji jest określona wzorem
A) 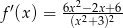 B)
B) 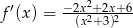 C)
C) 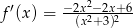 D)
D) 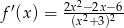
O zdarzeniach losowych 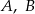 wiadomo, że:
wiadomo, że: 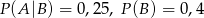 i
i 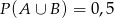 . Wtedy prawdopodobieństwo
. Wtedy prawdopodobieństwo 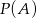 jest równe
jest równe
A) 0,1 B) 0,2 C) 0,3 D) 0,4
Zadania otwarte
Trzy koła o promieniu 1 są parami styczne zewnętrznie. Oblicz pole obszaru zawartego między tymi kołami.
Liczby  i
i 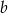 są rozwiązaniami równania
są rozwiązaniami równania 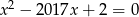 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia
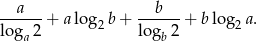
Ile jest liczb naturalnych ośmiocyfrowych, w których każda cyfra jest większa od 4 i dokładnie 3 spośród cyfr takiej liczby są równe 9?
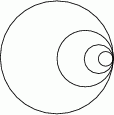
Dany jest okrąg 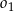 o promieniu
o promieniu  . Wewnątrz tego okręgu narysowano okrąg
. Wewnątrz tego okręgu narysowano okrąg 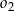 styczny wewnętrznie o średnicy
styczny wewnętrznie o średnicy  , wewnątrz okręgu
, wewnątrz okręgu 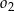 znów narysowano okrąg styczny wewnętrznie o średnicy
znów narysowano okrąg styczny wewnętrznie o średnicy 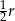 itd. Czynność tę powtórzono nieskończenie wiele razy. Oblicz sumę długości wszystkich skonstruowanych w ten sposób okręgów.
itd. Czynność tę powtórzono nieskończenie wiele razy. Oblicz sumę długości wszystkich skonstruowanych w ten sposób okręgów.
Wykaż, że jeżeli 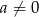 i
i 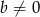 , to
, to 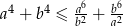 .
.
Rozwiąż nierówność 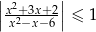 .
.
Funkcja 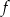 określona jest wzorem
określona jest wzorem 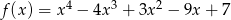 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania tych stycznych do wykresu funkcji
. Wyznacz równania tych stycznych do wykresu funkcji 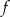 , które są równoległe do prostej o równaniu
, które są równoległe do prostej o równaniu 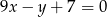 .
.
Dany jest trójkąt prostokątny o przyprostokątnych długości: 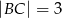 i
i 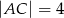 . Na boku
. Na boku 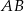 tego trójkąta wybrano taki punkt
tego trójkąta wybrano taki punkt 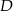 , że
, że 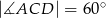 . Oblicz długość odcinka
. Oblicz długość odcinka 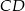 .
.
Rozwiąż nierówność 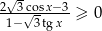 w przedziale
w przedziale 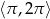 .
.
Podstawą ostrosłupa 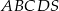 jest romb
jest romb 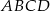 , w którym
, w którym 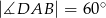 . Krawędź
. Krawędź 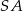 jest wysokością ostrosłupa oraz jej długość jest równa długości krawędzi podstawy. Oblicz sinus kąta nachylenia ściany
jest wysokością ostrosłupa oraz jej długość jest równa długości krawędzi podstawy. Oblicz sinus kąta nachylenia ściany 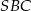 do płaszczyzny podstawy.
do płaszczyzny podstawy.
Punkty 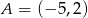 i
i 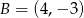 są wierzchołkami trójkąta
są wierzchołkami trójkąta 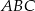 , a wysokości opuszczone z wierzchołków
, a wysokości opuszczone z wierzchołków 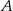 i
i 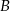 tego trójkąta zawierają się odpowiednio w prostych o równaniach
tego trójkąta zawierają się odpowiednio w prostych o równaniach 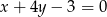 oraz
oraz 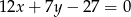 . Oblicz długość wysokości tego trójkąta opuszczonej na bok
. Oblicz długość wysokości tego trójkąta opuszczonej na bok 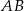 .
.
Na rysunku poniżej przedstawiono fragment wykresu funkcji 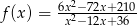 określonej dla
określonej dla 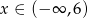 . Wykres ten przecina osie
. Wykres ten przecina osie 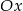 i
i 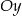 odpowiednio w punktach
odpowiednio w punktach 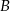 i
i 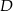 , a punkt
, a punkt 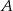 jest początkiem układu współrzędnych. Rozpatrujemy wszystkie czworokąty
jest początkiem układu współrzędnych. Rozpatrujemy wszystkie czworokąty 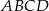 , w których punkt
, w których punkt 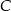 leży na wykresie funkcji
leży na wykresie funkcji 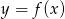 pomiędzy punktami
pomiędzy punktami 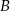 i
i 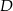 .
.
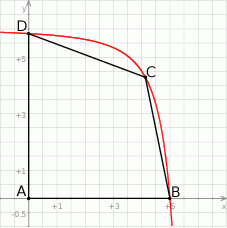
Oblicz pierwszą współrzędną wierzchołka 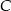 tego z rozpatrywanych czworokątów, którego pole jest największe.
tego z rozpatrywanych czworokątów, którego pole jest największe.

