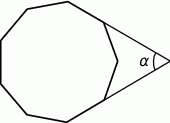
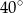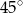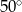Moneta o średnicy 1 cm toczy się po obwodzie sześciokąta foremnego o boku długości 1 cm (patrz rysunek) tak długo, aż powróci do położenia początkowego. Ile centymetrów ma długość drogi, którą zakreślił środek monety?
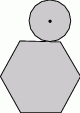
A) 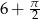 B)
B) 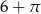 C)
C) 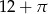 D)
D) 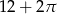 E)
E) 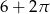

 takich, że odległość na osi liczbowej między liczbami
takich, że odległość na osi liczbowej między liczbami 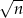 i 10 jest mniejsza niż 1.
i 10 jest mniejsza niż 1.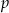 liczby
liczby 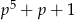 i
i 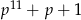 są pierwsze.
są pierwsze. 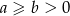 to
to 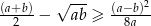 .
. 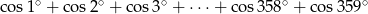 ?
?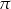
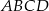 kolejno w punktach
kolejno w punktach 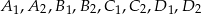 (zobacz rysunek).
(zobacz rysunek). 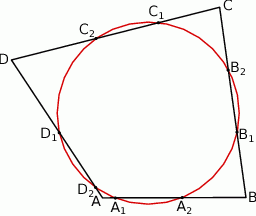
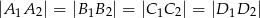 , to w czworokąt
, to w czworokąt 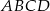 można wpisać okrąg.
można wpisać okrąg. 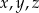 spełniona jest nierówność
spełniona jest nierówność 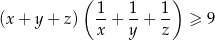
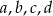 są liczbami dodatnimi to
są liczbami dodatnimi to 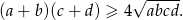

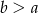 zachodzi równość
zachodzi równość 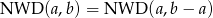 .
. 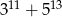 jest
jest 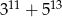
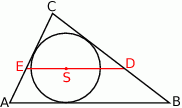
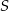 okręgu wpisanego w trójkąt
okręgu wpisanego w trójkąt 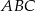 poprowadzono prostą równoległą do boku
poprowadzono prostą równoległą do boku 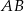 , która przecina boki
, która przecina boki 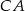 i
i 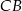 odpowiednio w punktach
odpowiednio w punktach 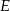 i
i 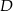 .
.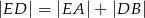 .
. 
 ?
?