Najprostsze równania wielomianowe to równania liniowe oraz kwadratowe. Ponieważ jednak omówiliśmy je w osobnych poradnikach, skupimy się teraz wyłącznie na równaniach stopnia co najmniej 3. Proste równania Bardzo wiele równań, które pojawiają się w zadaniach szkolnych, możemy rozwiązać bez korzystania z jakichkolwiek twierdzeń czy algorytmów. Ogólna zasada jest prosta: próbujemy równanie doprowadzić do postaci iloczyn prostych składników równy 0. Przez proste składniki rozumiemy wielomiany, dla których bardzo łatwo jest wyznaczyć pierwiastki, np. wielomiany liniowe 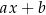 , albo kwadratowe
, albo kwadratowe 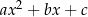 .
.
Rozwiążmy równanie 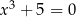 .
.
Liczymy
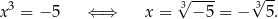
Zauważmy, że równanie jest na tyle proste, że nie ma tym przypadku potrzeby rozkładania wielomianu z lewej strony równania.
Rozwiążmy równanie 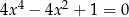 .
.
Jeżeli się dobrze przyjrzymy, to powinniśmy dostrzec, że z lewej strony mamy wzór skróconego mnożenia:
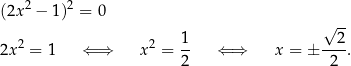
Rozwiążmy równanie 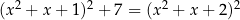 .
.
Korzystamy ze wzoru skróconego mnożenia na różnicę kwadratów.
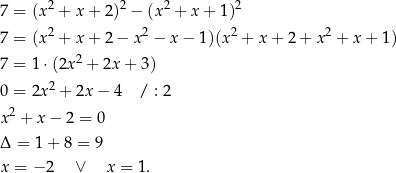
Grupowanie wyrazów Odrobinę więcej wprawy wymagają zadania, w których należy odpowiednio pogrupować składniki, tak aby móc wyłączyć dwumian postaci 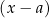 przed nawias.
przed nawias.
Rozwiążmy równanie 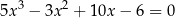 .
.
Zauważmy, że dwa ostatnie współczynniki: 10 i -6 to wielokrotności pierwszych dwóch współczynników: 5 i -3. Taka sytuacja to typowy znak, że możemy coś wyłączyć przed nawias.
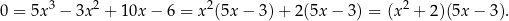
Mamy zatem 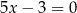 , czyli
, czyli 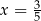 .
.
Rozwiążmy równanie 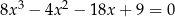 .
.
Tu już trochę trudniej dostrzec możliwość wyłączenia czynnika liniowego przed nawias, ale schemat jest ten sam, co poprzednio.
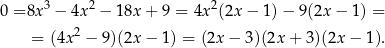
Mamy zatem 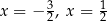 lub
lub 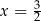 .
.
Pierwiastki wymierne No dobrze, a co zrobić, gdy nie uda nam się sprytnie rozłożyć wielomianu na czynniki? – stosujemy wtedy twierdzenie o wymiernych pierwiastkach wielomianu.
Jeżeli liczba wymierna 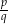 jest pierwiastkiem równania
jest pierwiastkiem równania
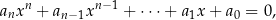
o współczynnikach całkowitych, oraz ułamek 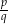 jest nieskracalny, to
jest nieskracalny, to 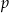 dzieli
dzieli 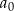 i
i 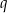 dzieli
dzieli 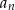 .
.
Powyższe twierdzenie daje nam przepis w jaki sposób poszukiwać pierwiastków wielomianu o współczynnikach całkowitych: szukamy pierwiastków (wstawiając do wielomianu) wśród liczb wymiernych postaci 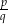 , gdzie
, gdzie 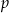 dzieli
dzieli 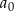 i
i 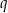 dzieli
dzieli 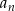 .
.
Wymierne pierwiastki równania 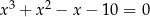 muszą być postaci:
muszą być postaci:
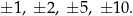
Sprawdzając po kolei te liczby, znajdujemy pierwiastek 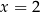 :
:
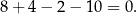
Wyznaczmy wymierne pierwiastki równania 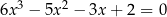 .
.
Na mocy powyższego twierdzenia musimy brać pod uwagę ułamki 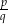 , gdzie
, gdzie 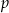 dzieli 2, a
dzieli 2, a 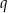 dzieli 6. Dzielniki 2 są cztery:
dzieli 6. Dzielniki 2 są cztery: 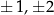 , a dzielników 6 jest 8:
, a dzielników 6 jest 8: 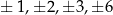 . Łatwo sprawdzić, że otrzymujemy w ten sposób następujące liczby
. Łatwo sprawdzić, że otrzymujemy w ten sposób następujące liczby
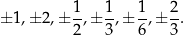
Można sprawdzić, że pierwiastkami są 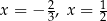 oraz
oraz 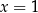 .
.
Gdy uda nam się już znaleźć chociaż jeden pierwiastek równania, korzystamy z tzw. twierdzenia Bézouta
Liczba  jest miejscem zerowym wielomianu
jest miejscem zerowym wielomianu 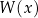 wtedy i tylko wtedy, gdy wielomian
wtedy i tylko wtedy, gdy wielomian 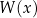 jest podzielny przez dwumian
jest podzielny przez dwumian 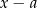 .
.
Z punktu widzenia rozwiązywania równania, twierdzenie to oznacza, że jeżeli wiemy, że liczba  jest pierwiastkiem równania
jest pierwiastkiem równania 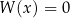 , to wielomian
, to wielomian 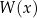 można podzielić przez dwumian
można podzielić przez dwumian 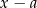 . Samo dzielenie wielomianów zostało opisane w osobnym poradniku. Gdy wykonamy dzielenie, otrzymamy ponownie równanie wielomianowe, ale jego stopień będzie już o jeden niższy.
. Samo dzielenie wielomianów zostało opisane w osobnym poradniku. Gdy wykonamy dzielenie, otrzymamy ponownie równanie wielomianowe, ale jego stopień będzie już o jeden niższy.
Rozwiążmy równanie 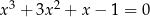 .
.
Najpierw szukamy pierwiastków wymiernych: nie mamy dużego wyboru musimy tylko sprawdzić 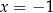 i
i 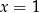 . Okazuje się, że pierwsza z tych liczb jest pierwiastkiem, więc dzielimy lewą stronę przez
. Okazuje się, że pierwsza z tych liczb jest pierwiastkiem, więc dzielimy lewą stronę przez 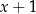 . Gdy to zrobimy otrzymamy
. Gdy to zrobimy otrzymamy
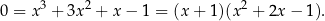
Pierwszy składnik zeruje się dokładnie dla 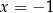 , a ten pierwiastek już znamy, więc wystarczy sprawdzić kiedy zeruje się drugi nawias, co prowadzi do zwykłego równania kwadratowego.
, a ten pierwiastek już znamy, więc wystarczy sprawdzić kiedy zeruje się drugi nawias, co prowadzi do zwykłego równania kwadratowego.
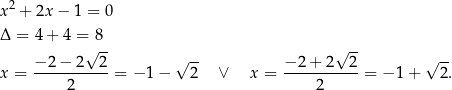
W sumie równanie ma więc trzy rozwiązania.

