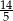Zadanie nr 8817125
Dane są punkty 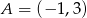 i
i 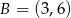 . Funkcja
. Funkcja 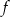 przyporządkowuje dowolnemu punktowi należącemu do odcinka
przyporządkowuje dowolnemu punktowi należącemu do odcinka 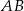 jego odległość od punktu
jego odległość od punktu 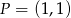 . Wyznacz zbiór wartości tej funkcji i jej wartość najmniejszą.
. Wyznacz zbiór wartości tej funkcji i jej wartość najmniejszą.
Rozwiązanie
Sposób I
Na początku musimy jakoś opisać punkty odcinka 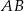 (mądrzej mówiąc, sparametryzujemy odcinek
(mądrzej mówiąc, sparametryzujemy odcinek 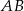 ). Napiszmy równanie prostej
). Napiszmy równanie prostej 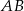 . Szukamy prostej w postaci
. Szukamy prostej w postaci 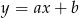 . Podstawiając współrzędne punktów
. Podstawiając współrzędne punktów 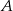 i
i 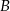 otrzymujemy układ
otrzymujemy układ
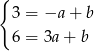
Odejmujemy od drugiego równania pierwsze (żeby skrócić 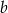 ) i mamy
) i mamy
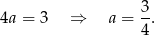
Zatem 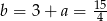 i prosta
i prosta 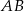 ma równanie
ma równanie 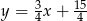 . Zauważmy teraz, że punkt
. Zauważmy teraz, że punkt 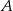 otrzymamy podstawiając
otrzymamy podstawiając 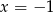 , a punkt
, a punkt 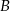 podstawiając
podstawiając 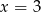 , więc dowolny punkt
, więc dowolny punkt 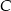 odcinka
odcinka 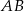 ma postać
ma postać 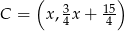 , gdzie
, gdzie 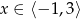 .
.
Obliczmy teraz odległość 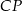 .
.
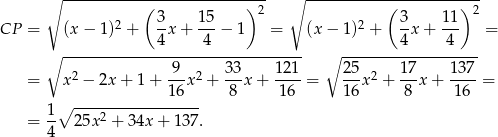
Ponieważ pierwiastek 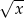 jest funkcją rosnącą, wystarczy badać funkcję pod pierwiastkiem, a na koniec policzyć pierwiastki z otrzymanych wartości. Funkcja
jest funkcją rosnącą, wystarczy badać funkcję pod pierwiastkiem, a na koniec policzyć pierwiastki z otrzymanych wartości. Funkcja 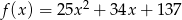 dla
dla 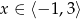 jest fragmentem paraboli o ramionach skierowanych do góry. Sprawdźmy gdzie jest jej wierzchołek.
jest fragmentem paraboli o ramionach skierowanych do góry. Sprawdźmy gdzie jest jej wierzchołek.
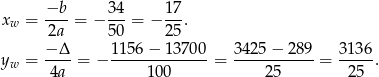
Ponieważ 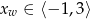 , dokładnie w tym punkcie funkcja
, dokładnie w tym punkcie funkcja 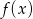 przyjmuje wartość najmniejszą. Pamiętając o wyciągnięciu pierwiastka i podzieleniu przez 4, wartość najmniejsza wyjściowej funkcji będzie równa
przyjmuje wartość najmniejszą. Pamiętając o wyciągnięciu pierwiastka i podzieleniu przez 4, wartość najmniejsza wyjściowej funkcji będzie równa 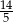 .
.
Aby ustalić jaki jest zbiór wartości, liczymy wartości na końcach przedziału.
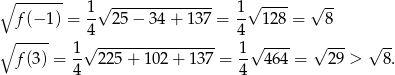
Zatem zbiór wartości to przedział
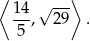
Sposób II
Zauważmy, że każdy punkt 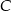 odcinka
odcinka 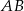 jest postaci
jest postaci
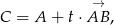
gdzie 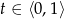 (ten zapis oznacza przesunięcie punktu
(ten zapis oznacza przesunięcie punktu 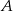 o wektor
o wektor 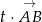 ). Np. dla
). Np. dla 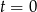 mamy punkt
mamy punkt 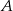 , dla
, dla 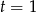 punkt
punkt 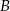 , a dla
, a dla 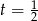 środek odcinka
środek odcinka 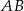 . Rozpiszmy dokładniej tę równość
. Rozpiszmy dokładniej tę równość
![C = (− 1,3)+ t[2,3] = (− 1,3) + [4t,3t] = (4t− 1 ,3t+ 3).](https://img.zadania.info/zad/8817125/HzadR43x.gif)
Inny sposób otrzymania takiej parametryzacji odcinka 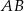 to obserwajca, że
to obserwajca, że
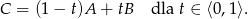
Tak jest, bo ten wzór jest równaniem prostej przechodzącej przez punkty 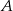 (dla
(dla 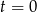 ) i
) i 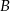 (dla
(dla 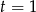 ). Dla pośrednich wartości
). Dla pośrednich wartości 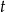 otrzymujemy punkty odcinka
otrzymujemy punkty odcinka 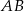 . (Tak naprawdę wyprowadziliśmy tzw. parametryczne równanie prostej).
. (Tak naprawdę wyprowadziliśmy tzw. parametryczne równanie prostej).
Dobrze, skoro wiemy jak wyglądają punkty odcinka 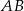 , to możemy policzyć odległość
, to możemy policzyć odległość 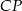 .
.
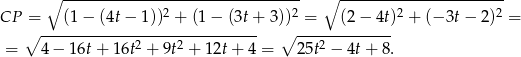
Ponieważ pierwiastek 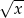 jest funkcją rosnącą, wystarczy badać funkcję pod pierwiastkiem, a na koniec policzyć pierwiastki z otrzymanych wartości. Funkcja
jest funkcją rosnącą, wystarczy badać funkcję pod pierwiastkiem, a na koniec policzyć pierwiastki z otrzymanych wartości. Funkcja 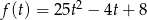 dla
dla 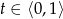 jest fragmentem paraboli o ramionach skierowanych do góry. Sprawdźmy gdzie jest jej wierzchołek.
jest fragmentem paraboli o ramionach skierowanych do góry. Sprawdźmy gdzie jest jej wierzchołek.
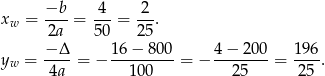
Ponieważ 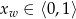 , dokładnie w tym punkcie funkcja
, dokładnie w tym punkcie funkcja 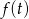 przyjmuje wartość najmniejszą. Pamiętając o wyciągnięciu pierwiastka, wartość najmniejsza wyjściowej funkcji będzie równa
przyjmuje wartość najmniejszą. Pamiętając o wyciągnięciu pierwiastka, wartość najmniejsza wyjściowej funkcji będzie równa 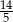 .
.
Aby ustalić jaki jest zbiór wartości, liczymy wartości na końcach przedziału.
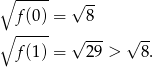
Zatem zbiór wartości to przedział
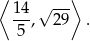
Odpowiedź: Zbiór wartości: 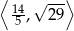 , wartość najmniejsza:
, wartość najmniejsza: