Zadanie nr 9935069

Okrąg wpisany w trójkąt 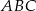ABC jest styczny do boków 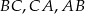BC ,CA ,AB odpowiednio w punktach 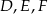D ,E,F . Punkty 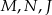M ,N ,J są odpo- wiednio środkami okręgów wpisanych w trójkąty 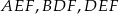AEF ,BDF ,DEF . Dowieść, że punkty 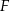i 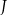są symetryczne względem prostej .

Wersja PDF

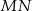Rozwiązanie

W tym zadaniu (jak to często w geometrii) najważniejszy jest rysunek – to on powie nam co mamy robić.

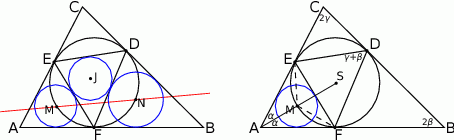
Gdy dokładnie narysujemy opisaną sytuację, to pierwsza rzecz która się narzuca, to że punkty 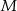i 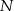leżą na okręgu wpisanym w trójkąt 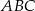ABC . Zanim zaczniemy kombinować do czego to się może przydać, spróbujmy sprawdzić czy tak jest (prawy rysunek).

To co musimy sprawdzić, to czy 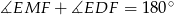∘ ∡EMF + ∡EDF = 18 0 (bo to jest warunek na to, aby punkt 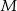leżał na okręgu opisanym na trójkącie 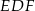EDF , albo jak ktoś woli na to, żeby na czworokącie 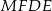MF DE można było opisać okrąg). Oba kąty łatwo jest wyliczyć korzystając z tego, że trójkąty 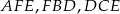AF E ,FBD ,DCE są równoramienne. Jeżeli oznaczymy kąty jak na rysunku to mamy

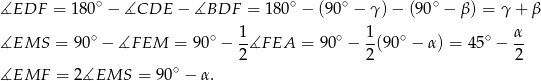
∘ ∘ ∘ ∘ ∡EDF = 180 − ∡CDE − ∡BDF = 180 − (9 0 − γ)− (90 − β) = γ + β ∘ ∘ 1- ∘ 1- ∘ ∘ α- ∡EMS = 90 − ∡F EM = 90 − 2∡F EA = 90 − 2(90 − α ) = 45 − 2 ∡EMF = 2∡EMS = 90 ∘ − α .

Jest więc jasne, że 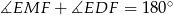∡EMF + ∡EDF = 180∘ , czyli punkt 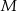leży na okręgu wpisanym w trójkąt 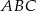ABC . Oczywiście podobnie jest z punktem 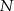. Zanim przejdziemy dalej, zauważmy jeszcze, że punkt 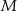dzieli łuk 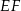na połowy, a punkt 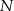dzieli na połowy łuk .

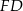Ok, teraz z powrotem popatrzmy na wyjściowy obrazek i się zastanówmy co dalej robić.

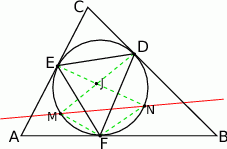
Ponieważ punkt 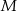dzieli łuk 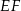na połowy, prosta 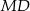jest dwusieczną kąta 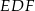EDF . Zatem leży na niej punkt 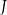. Podobnie, punkty 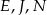E,J,N są współliniowe. Ponadto, z tych samych powodów, prosta 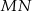jest dwusieczną kąta 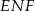ENF oraz kąta 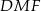DMF . Zatem czworokąt 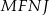MF NJ musi być deltoidem, co dowodzi, że punkty 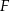i 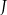są symetryczne względem prostej .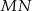