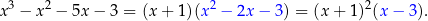Dzielenie wielomianów to motyw przewodni wielu szkolnych zadań. Zacznijmy od przypomnienia co to jest dzielenie liczb. Co to znaczy podzielić 15 przez 7? To znaczy sprawdzić ile razy 7 mieści się w 15 (to jest iloraz), oraz ile zostanie jak te wszystkie możliwe siódemki odejmiemy (to jest reszta). Możemy to działanie zapisać w postaci
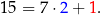
W powyższym rachunku 2 jest ilorazem, a 1 resztą z dzielenia. To co jest bardzo ważne, to że reszta jest zawsze mniejsza od liczby, przez którą dzielimy (gdyby reszta była większa od 7 to by znaczyło, że w danej liczbie mieści się jeszcze jedna siódemka, czyli jest coś nie tak z naszym dzieleniem).
Dokładnie tak samo dzieli się wielomiany i jeżeli będziemy musieli sobie kiedyś szybko przypomnieć o co chodzi w dzieleniu wielomianów, najpierw napiszmy sobie przykład z liczbami podobny do tego wyżej.
Podzielenie wielomianu 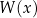 przez wielomian
przez wielomian 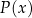 polega na znalezieniu dwóch wielomianów
polega na znalezieniu dwóch wielomianów 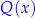 i
i 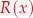 tak, aby była spełniona równość:
tak, aby była spełniona równość:
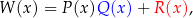
gdzie stopień wielomianu 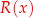 jest mniejszy od stopnia wielomianu
jest mniejszy od stopnia wielomianu 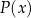 . Wielomian
. Wielomian 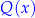 nazywamy ilorazem, a
nazywamy ilorazem, a 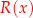 resztą z dzielenia. Warunek
resztą z dzielenia. Warunek 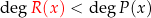 należy traktować jako dokładny odpowiednik analogicznego warunku dla reszty przy dzieleniu liczb (gdyby stopień nie był mniejszy, to by znaczyło, że resztę wciąż można podzielić przez
należy traktować jako dokładny odpowiednik analogicznego warunku dla reszty przy dzieleniu liczb (gdyby stopień nie był mniejszy, to by znaczyło, że resztę wciąż można podzielić przez 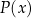 , co byłoby sprzeczne z ideą reszty).
, co byłoby sprzeczne z ideą reszty).
Powiedzmy, że chcemy podzielić wielomian 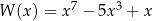 przez wielomian
przez wielomian 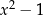 . Jakie będą stopnie ilorazu i reszty?
. Jakie będą stopnie ilorazu i reszty?
Stopień ilorazu łatwo przewidzieć. Ponieważ stopnie się dodają gdy mnożymy wielomiany, iloraz musi mieć stopień 5 (inaczej mówiąc, żeby wyszło 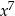 musimy
musimy 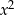 przemnożyć przez
przemnożyć przez 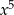 ). Co do reszty, to wiemy, że maksymalnie może mieć stopień 1 (bo dzielimy przez wielomian stopnia 2). Czy ma dokładnie stopień 1? Tego już nie wiadomo, trzeba podzielić, żeby się przekonać.
). Co do reszty, to wiemy, że maksymalnie może mieć stopień 1 (bo dzielimy przez wielomian stopnia 2). Czy ma dokładnie stopień 1? Tego już nie wiadomo, trzeba podzielić, żeby się przekonać.
Wyznaczmy resztę z dzielenia wielomianu 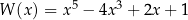 przez wielomian
przez wielomian 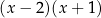 .
.
Ponieważ dzielimy przez wielomian stopnia 2, reszta będzie miała stopień 1, czyli szukamy wielomianu 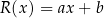 takiego, że
takiego, że
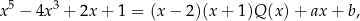
gdzie 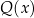 jest pewnym wielomianem, który nas specjalnie nie interesuje (bo mamy tylko wyznaczyć resztę). Podstawiając w tej równości
jest pewnym wielomianem, który nas specjalnie nie interesuje (bo mamy tylko wyznaczyć resztę). Podstawiając w tej równości 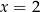 i
i 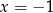 (żeby składnik z
(żeby składnik z 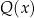 się wyzerował), otrzymujemy układ równań
się wyzerował), otrzymujemy układ równań
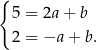
Odejmując od pierwszego równania drugie otrzymamy 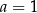 , skąd
, skąd 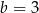 i
i 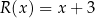 .
.
W przypadku gdy 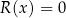 mówimy, że wielomian
mówimy, że wielomian 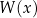 dzieli się przez
dzieli się przez 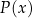 bez reszty (albo krótko, że się dzieli przez
bez reszty (albo krótko, że się dzieli przez 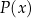 ). Oczywiście znowu jest to w pełni analogiczne do terminologii stosowanej przy dzieleniu liczb.
). Oczywiście znowu jest to w pełni analogiczne do terminologii stosowanej przy dzieleniu liczb.
W jednym z poprzednich przykładów sprawdziliśmy, że
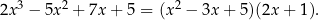
Równość ta oznacza, że wielomian z lewej strony dzieli się bez reszty zarówno przez wielomian 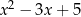 (z ilorazem
(z ilorazem 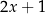 ) jak i przez
) jak i przez 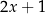 (z ilorazem
(z ilorazem 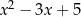 ).
).
Dzielenie wielomianów – dzielenie pisemne Skoro już dobrze wiemy o co chodzi w dzieleniu wielomianów, nadszedł czas, żebyśmy nauczyli się sprawnie takie dzielenie wykonywać.
Naukę rozpoczniemy od dzielenia pisemnego, które jest dokładnym odpowiednikiem dzielenia liczb. Powiedzmy, że chcemy podzielić wielomian 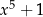 przez wielomian
przez wielomian 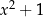 . Wykonamy najpierw dzielenie, a potem wyjaśnimy, co dokładnie się działo.
. Wykonamy najpierw dzielenie, a potem wyjaśnimy, co dokładnie się działo.
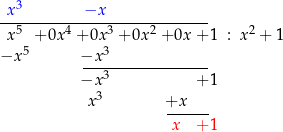
Zaczynamy jak przy dzieleniu liczb: piszemy wielomian, który dzielimy i nad nim rysujemy kreskę. W tym kroku jest ważne, żeby napisać wszystkie współczynniki wielomianu, również te zerowe. Patrzymy teraz na najwyższą potęgę  w naszym wielomianie, czyli na
w naszym wielomianie, czyli na 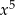 i dzielimy przez najwyższą potęgę
i dzielimy przez najwyższą potęgę  w wielomianie przez, który dzielimy. Otrzymujemy
w wielomianie przez, który dzielimy. Otrzymujemy 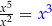 i piszemy to nad kreską, jest to pierwszy składnik wyniku. Mnożymy teraz otrzymane
i piszemy to nad kreską, jest to pierwszy składnik wyniku. Mnożymy teraz otrzymane 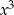 przez wielomian, przez który dzielimy i otrzymujemy
przez wielomian, przez który dzielimy i otrzymujemy
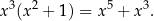
Zapisujemy to wyrażenie ze zmienionym znakiem pod wyjściowym wielomianem. Całość podkreślamy i dodajemy. Teraz startujemy od wyrażenia pod kreską, czyli od 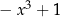 i powtarzamy te same operacje co poprzednio: dzielimy
i powtarzamy te same operacje co poprzednio: dzielimy 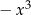 przez
przez 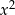 i wynik
i wynik 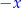 piszemy u góry; przemnażamy
piszemy u góry; przemnażamy 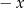 przez
przez 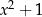 i podpisujemy ze zmienionym znakiem pod
i podpisujemy ze zmienionym znakiem pod 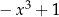 . Znowu kreska i dodawanie. Teraz otrzymujemy już wielomian, którego stopień jest mniejszy od wielomianu, przez który dzielimy, więc jest to nasza reszta. Iloraz mamy napisany na samej górze.
. Znowu kreska i dodawanie. Teraz otrzymujemy już wielomian, którego stopień jest mniejszy od wielomianu, przez który dzielimy, więc jest to nasza reszta. Iloraz mamy napisany na samej górze.
Sprawdźmy jeszcze, że dzielenie dało nam dobry wynik
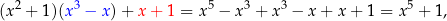
czyli jest OK.
Dzielenie pisemne to bardzo szybki sposób na dzielenie wielomianów, ale zapis algorytmu jest dość nieprzyjemny i z tego powodu na ogół traktujemy je jak ostateczność. Dzielenie wielomianów – grupowanie wyrazów Grupowanie wyrazów to często najprostszy sposób na dzielenie wielomianów. Wprawdzie sposób ten nie jest najszybszy, ale ma dość elegancki zapis i najtrudniej się w nim pomylić. A nawet gdy zrobimy błąd, to dość łatwo jest go znaleźć.
Ale do rzeczy, zróbmy ten sam przykład co przy dzieleniu pisemnym.
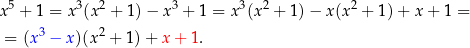
W zasadzie jest to inny zapis dzielenia pisemnego: zaczynamy od najwyższej potęgi, czyli od 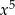 i dopisujemy do niej składniki tak, aby mieć wielokrotność wielomianu, przez który dzielimy, czyli
i dopisujemy do niej składniki tak, aby mieć wielokrotność wielomianu, przez który dzielimy, czyli 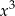 . Potem odejmujemy to dopisane
. Potem odejmujemy to dopisane 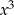 i resztę przepisujemy bez zmian. W kolejnym kroku robimy to samo, ale początkowym składnikiem
i resztę przepisujemy bez zmian. W kolejnym kroku robimy to samo, ale początkowym składnikiem 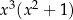 już się nie zajmujemy i zaczynamy od
już się nie zajmujemy i zaczynamy od 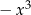 . Znowu dopisujemy brakujący składnik do tego, żeby mieć wielokrotność
. Znowu dopisujemy brakujący składnik do tego, żeby mieć wielokrotność 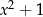 i go odejmujemy, żeby się zgadzało. Zostaje wielomian stopnia 1, więc jest to już reszta z dzielenia. Na koniec grupujemy wyrazy wyciągając
i go odejmujemy, żeby się zgadzało. Zostaje wielomian stopnia 1, więc jest to już reszta z dzielenia. Na koniec grupujemy wyrazy wyciągając 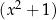 przed nawias, żeby było widać jaki jest iloraz.
przed nawias, żeby było widać jaki jest iloraz.
Przy odrobinie wprawy, zapis dzielenia przy pomocy grupowania wyrazów można znacznie skrócić, co zilustrujmy dzieląc wielomian 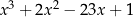 przez wielomian
przez wielomian 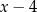 .
.
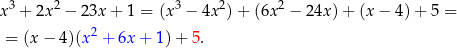
O co chodzi? Rozpiszmy szczegółowo w jaki sposób pisaliśmy kolejne składniki tego wyrażania.
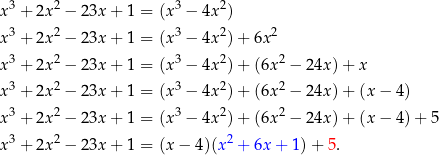
Zaczynamy od 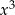 i dopisujemy drugi składnik tak, aby mieć wielomian podzielny przez
i dopisujemy drugi składnik tak, aby mieć wielomian podzielny przez 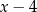 (czyli
(czyli 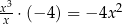 ). Potem patrzymy na
). Potem patrzymy na 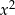 : ma być
: ma być 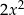 , a na razie mamy napisane
, a na razie mamy napisane 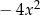 , więc trzeba dodać
, więc trzeba dodać 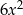 . Do tego
. Do tego 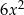 znowu dopisujemy składnik tak, aby mieć wielomian podzielny przez
znowu dopisujemy składnik tak, aby mieć wielomian podzielny przez 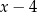 (czyli
(czyli 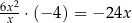 ). Teraz patrzymy na
). Teraz patrzymy na  : mamy napisane
: mamy napisane 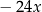 , a ma być
, a ma być 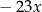 , więc dopisujemy
, więc dopisujemy  . Potem dopisujemy
. Potem dopisujemy 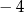 (żeby mieć
(żeby mieć 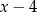 ) i na koniec dodajemy 5, żeby się zgadzało (bo ma być 1). Na koniec wyłączamy
) i na koniec dodajemy 5, żeby się zgadzało (bo ma być 1). Na koniec wyłączamy 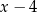 przed nawias. Dzielenie wielomianów – schemat Hornera Schemat Hornera pozwala bardzo szybko (i bezmyślnie) dzielić wielomiany przez dwumiany postaci
przed nawias. Dzielenie wielomianów – schemat Hornera Schemat Hornera pozwala bardzo szybko (i bezmyślnie) dzielić wielomiany przez dwumiany postaci 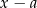 . Jak zwykle wyjaśnijmy o co chodzi na przykładzie.
. Jak zwykle wyjaśnijmy o co chodzi na przykładzie.
Wykonamy to samo dzielnie, co poprzednio, czyli dzielimy 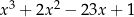 przez
przez 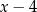 . Robimy tabelkę i w pierwszym jej wierszu, począwszy od drugiego pola, wpisujemy kolejne współczynniki wielomianu (łącznie z zerowymi!), który dzielimy.
. Robimy tabelkę i w pierwszym jej wierszu, począwszy od drugiego pola, wpisujemy kolejne współczynniki wielomianu (łącznie z zerowymi!), który dzielimy.
| 1 | 2 | -23 | 1 | |
| 4 | 1 | 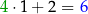 | 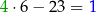 | 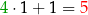 |
Dolny wiersz wypełniamy następująco:
-
w pierwszym polu wpisujemy
 , jeżeli dzielimy przez
, jeżeli dzielimy przez 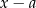 (w naszym przypadku 4);
(w naszym przypadku 4); -
w drugim polu przepisujemy element z górnego wiersza (w naszym przypadku 1);
-
każdy kolejny element drugiego wiersza powstaje przez pomnożenie poprzedniego elementu przez element pierwszy (czyli przez
 , u nas przez 4) i dodanie liczby, która jest napisana u góry.
, u nas przez 4) i dodanie liczby, która jest napisana u góry.
Gdy już wypełnimy dolny wiersz, wynik odczytujemy następująco
-
liczby od drugiej do przedostatniej są współczynnikami ilorazu, w naszym przykładzie dają nam wielomian
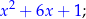
-
ostatnia liczba w drugim wierszu jest resztą z dzielenia, w naszym przykładzie reszta jest równa 5.
Widać zatem, że otrzymaliśmy tę samą odpowiedź, co poprzednio:
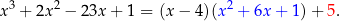
Sprawdźmy, że liczba 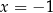 jest pierwiastkiem podwójnym wielomianu
jest pierwiastkiem podwójnym wielomianu 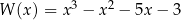 .
.
Musimy wykazać, że wielomian 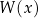 dzieli się przez
dzieli się przez 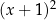 , czyli, że można go dwa razy podzielić przez dwumian
, czyli, że można go dwa razy podzielić przez dwumian 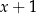 . Wykonujemy pierwsze dzielenie.
. Wykonujemy pierwsze dzielenie.
| 1 | -1 | -5 | -3 | |
| -1 | 1 | -2 | -3 | 0 |
Zatem po podzieleniu otrzymujemy wielomian 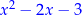 . Teraz dzielimy raz jeszcze.
. Teraz dzielimy raz jeszcze.
| 1 | -2 | -3 | |
| -1 | 1 | -3 | 0 |
Teraz otrzymaliśmy iloraz  i resztę 0, co pokazuje, że istotnie wyjściowy wielomian dzieli się przez
i resztę 0, co pokazuje, że istotnie wyjściowy wielomian dzieli się przez 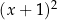 . Wynik wykonanych rachunków możemy zapisać w postaci:
. Wynik wykonanych rachunków możemy zapisać w postaci: