Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo dwukrotnego otrzymania liczby oczek różnej od 5 jest równe
A)  B)
B) 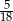 C)
C) 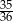 D)
D) 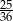
/Szkoła średnia/Zadania testowe/Prawdopodobieństwo/Kostki
Rzucamy sześć razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo otrzymania sześciu różnych liczb oczek, jest równe
A) 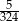 B)
B) 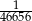 C)
C)  D)
D) 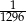
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo otrzymania sumy oczek równej trzy wynosi
A)  B)
B) 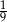 C)
C) 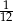 D)
D) 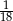
Prawdopodobieństwo zdarzenia, że w rzucie dwiema symetrycznymi kostkami do gry otrzymamy sumę oczek równą 6, wynosi
A) 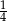 B)
B) 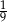 C)
C) 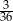 D)
D) 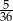
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo dwukrotnego otrzymania pięciu oczek jest równe
A)  B)
B) 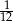 C)
C) 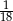 D)
D) 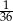
Prawdopodobieństwo zdarzenia, że w rzucie dwiema symetrycznymi kostkami do gry otrzymamy iloczyn oczek równy 4, wynosi
A) 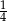 B)
B) 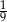 C)
C) 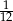 D)
D) 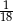
Prawdopodobieństwo zdarzenia, że w rzucie dwiema symetrycznymi kostkami do gry otrzymamy sumę oczek równą 7, wynosi
A)  B)
B) 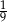 C)
C) 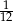 D)
D) 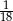
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo otrzymania parzystej sumy oczek jest równe
A)  B)
B) 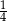 C)
C) 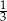 D)
D) 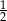
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo otrzymania pary liczb, których iloczyn jest większy od 18, jest równe
A) 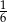 B)
B) 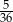 C)
C) 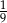 D)
D) 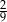
Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego oczka do sześciu oczek. Prawdopodobieństwo zdarzenia polegającego na tym, że iloczyn liczb wyrzuconych oczek jest liczbą nieparzystą, jest równe
A) 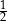 B)
B) 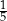 C)
C)  D)
D) 
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo otrzymania sumy oczek równej cztery wynosi
A)  B)
B) 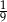 C)
C) 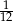 D)
D) 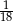
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo otrzymania pary liczb, których iloczyn jest większy od 20, jest równe
A) 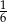 B)
B) 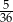 C)
C) 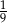 D)
D) 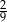
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo otrzymania iloczynu oczek równego cztery jest równe
A) 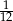 B)
B) 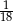 C)
C) 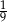 D)
D) 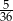
Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego do sześciu. Niech 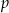 oznacza prawdopodobieństwo otrzymania w drugim rzucie liczby oczek podzielnej przez 3. Wtedy
oznacza prawdopodobieństwo otrzymania w drugim rzucie liczby oczek podzielnej przez 3. Wtedy
A) 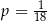 B)
B) 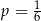 C)
C) 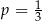 D)
D) 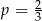
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Niech 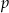 oznacza prawdopodobieństwo zdarzenia, że iloczyn liczb wyrzuconych oczek jest równy 5. Wtedy
oznacza prawdopodobieństwo zdarzenia, że iloczyn liczb wyrzuconych oczek jest równy 5. Wtedy
A) 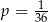 B)
B) 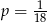 C)
C) 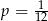 D)
D) 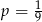
Losujemy rzucając dwukrotnie symetryczną kostką sześcienną. Jakie jest prawdopodobieństwo, że w drugim rzucie wylosujemy o trzy oczka więcej niż w pierwszym?
A) 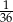 B)
B) 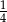 C)
C) 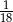 D)
D) 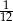
Prawdopodobieństwo zdarzenia, że w rzucie dwiema symetrycznymi kostkami do gry otrzymamy iloczyn oczek równy 6, wynosi
A) 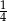 B)
B) 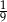 C)
C) 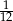 D)
D) 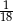
Rzucamy dwa razy sześcienną kostką do gry. Prawdopodobieństwo wyrzucenia w obu rzutach liczby oczek podzielnej przez 3 jest równe
A) 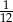 B)
B) 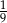 C)
C) 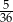 D)
D) 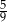
Rzucamy jeden raz symetryczną sześcienną kostką do gry. Niech 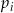 oznacza prawdopodobieństwo wyrzucenia liczby oczek podzielnej przez
oznacza prawdopodobieństwo wyrzucenia liczby oczek podzielnej przez 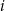 . Wtedy
. Wtedy
A) 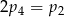 B)
B) 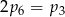 C)
C) 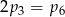 D)
D) 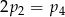
Rzucamy jeden raz symetryczną sześcienną kostką do gry. Niech 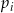 oznacza prawdopodobieństwo wyrzucenia liczby oczek podzielnej przez
oznacza prawdopodobieństwo wyrzucenia liczby oczek podzielnej przez 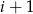 . Wtedy
. Wtedy
A) 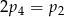 B)
B) 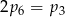 C)
C) 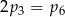 D)
D) 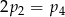
Rzucamy dwa razy sześcienną kostką do gry. Niech 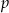 oznacza prawdopodobieństwo tego, że iloczyn liczb otrzymanych oczek dzieli się przez 6. Wtedy
oznacza prawdopodobieństwo tego, że iloczyn liczb otrzymanych oczek dzieli się przez 6. Wtedy
A) 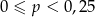 B)
B) 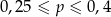 C)
C) 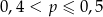 D)
D) 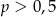
Rzucamy czterokrotnie sześcienną kostką do gry. Prawdopodobieństwo zdarzenia, że suma oczek wyrzuconych w czterech rzutach jest różna od 23 jest równe
A) 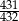 B)
B) 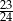 C)
C) 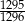 D)
D) 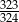
Rzucamy dwiema kostkami do gry. Jeśli 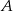 oznacza zdarzenie „suma wyrzuconych oczek jest równa 11”, a
oznacza zdarzenie „suma wyrzuconych oczek jest równa 11”, a 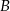 oznacza zdarzenie „suma wyrzuconych oczek jest równa 9” to
oznacza zdarzenie „suma wyrzuconych oczek jest równa 9” to
A) 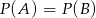 B)
B) 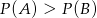 C)
C) 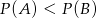 D)
D) 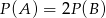
Rzucamy dwiema kostkami do gry. Jeśli 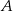 oznacza zdarzenie „suma wyrzuconych oczek jest równa 10”, a
oznacza zdarzenie „suma wyrzuconych oczek jest równa 10”, a 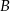 oznacza zdarzenie „suma wyrzuconych oczek jest równa 8” to
oznacza zdarzenie „suma wyrzuconych oczek jest równa 8” to
A) 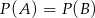 B)
B) 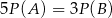 C)
C)  D)
D) 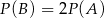
Rzucamy dwiema kostkami do gry. Jeśli 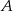 oznacza zdarzenie „suma wyrzuconych oczek jest równa 6”, a
oznacza zdarzenie „suma wyrzuconych oczek jest równa 6”, a 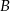 oznacza zdarzenie „suma wyrzuconych oczek jest równa 10” to
oznacza zdarzenie „suma wyrzuconych oczek jest równa 10” to
A) 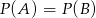 B)
B) 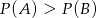 C)
C) 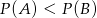 D)
D) 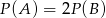
Rzucamy dwiema kostkami do gry. Jeśli 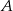 oznacza zdarzenie „suma wyrzuconych oczek jest równa 10”, a
oznacza zdarzenie „suma wyrzuconych oczek jest równa 10”, a 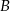 oznacza zdarzenie „suma wyrzuconych oczek jest równa 11” to
oznacza zdarzenie „suma wyrzuconych oczek jest równa 11” to
A) 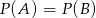 B)
B) 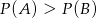 C)
C) 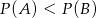 D)
D) 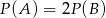
Rzucamy dwiema sześciennymi kostkami do gry. Prawdopodobieństwo tego, że suma wyrzuconych oczek wyniesie co najwyżej 9, jest równe
A) 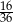 B)
B) 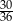 C)
C) 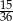 D)
D) 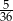
Rzucamy dwiema sześciennymi kostkami do gry. Prawdopodobieństwo tego, że suma wyrzuconych oczek wyniesie co najmniej 5, jest równe
A) 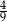 B)
B) 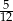 C)
C)  D)
D) 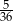
Rzucamy dwiema sześciennymi kostkami do gry. Prawdopodobieństwo tego, że suma wyrzuconych oczek wyniesie co najwyżej 10, jest równe
A) 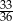 B)
B) 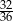 C)
C) 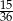 D)
D) 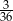
Rzucamy dwukrotnie sześcienną kostką do gry. Prawdopodobieństwo zdarzenia, że na każdej kostce wypadną co najmniej 4 oczka, jest równe
A) 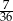 B)
B) 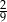 C)
C) 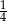 D)
D) 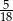
Rzucamy dwukrotnie sześcienną kostką do gry. Prawdopodobieństwo zdarzenia, że na każdej kostce wypadnie co najmniej 5 oczek, jest równe
A) 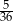 B)
B) 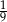 C)
C) 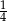 D)
D) 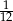
Rzucamy dwukrotnie sześcienną kostką do gry. Prawdopodobieństwo zdarzenia, że na każdej kostce wypadną co najwyżej 3 oczka, jest równe
A) 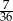 B)
B) 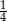 C)
C) 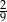 D)
D) 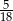
Rzucamy sześć razy symetryczną sześcienną kostką do gry. Niech 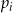 oznacza prawdopodobieństwo wyrzucenia
oznacza prawdopodobieństwo wyrzucenia 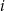 oczek w
oczek w 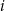 -tym rzucie. Wtedy
-tym rzucie. Wtedy
A) 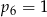 B)
B) 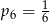 C)
C) 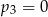 D)
D) 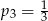
Rzucamy sześć razy symetryczną sześcienną kostką do gry. Niech 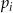 oznacza prawdopodobieństwo wyrzucenia mniej niż
oznacza prawdopodobieństwo wyrzucenia mniej niż 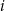 oczek w
oczek w 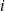 -tym rzucie. Wtedy
-tym rzucie. Wtedy
A) 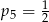 B)
B) 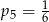 C)
C) 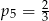 D)
D) 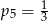
Kasia wykonała rzut trzema sześciennymi kostkami do gry i otrzymała sumę oczek większą niż 16. Prawdopodobieństwo, że Kasia wyrzuciła trzy szóstki jest równe
A) 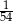 B)
B)  C)
C) 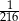 D)
D) 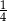
Jacek wykonał rzut trzema sześciennymi kostkami do gry i otrzymał sumę oczek mniejszą niż 5. Prawdopodobieństwo, że Jacek wyrzucił przynajmniej jedną dwójkę jest równe
A) 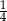 B)
B)  C)
C)  D)
D) 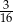
Rzucamy dwa razy sześcienną kostką do gry. Prawdopodobieństwo wyrzucenia co najmniej raz liczby oczek podzielnej przez 3 jest równe
A) 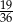 B)
B) 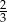 C)
C) 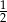 D)
D) 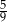
Rzucamy dwa razy sześcienną kostką do gry. Prawdopodobieństwo wyrzucenia co najmniej raz liczby oczek większej od 4 jest równe
A) 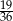 B)
B) 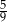 C)
C) 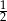 D)
D) 
Rzucamy dwa razy sześcienną kostką do gry. Prawdopodobieństwo otrzymania co najmniej raz pięciu oczek jest równe
A) 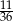 B)
B) 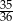 C)
C) 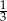 D)
D) 

