Zadanie nr 4835923
W trójkącie prostokątnym, w którym przyprostokątne mają długości 2 i 4, jeden z kątów ostrych ma miarę  . Oblicz
. Oblicz 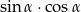 .
.
Rozwiązanie
Naszkicujmy trójkąt prostokątny.
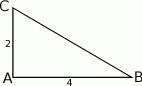
Długość przeciwprostokątnej 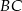 wyliczamy z twierdzenia Pitagorasa
wyliczamy z twierdzenia Pitagorasa
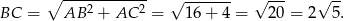
Zatem interesujące nas wyrażenie jest równe
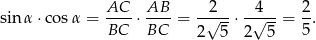
Zauważmy, że w powyższym rachunku nie miało znaczenia, który z kątów ostrych trójkąta jest równy  .
.
Odpowiedź: 

