Zadanie nr 5391420
Rozważamy wszystkie proste na płaszczyźnie, które są jednocześnie styczne do wykresu funkcji homograficznej 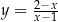 oraz do okręgu o równaniu
oraz do okręgu o równaniu 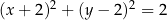 . Wyznacz równania tych spośród rozważanych prostych, których współczynniki kierunkowe są liczbami wymiernymi.
. Wyznacz równania tych spośród rozważanych prostych, których współczynniki kierunkowe są liczbami wymiernymi.
Rozwiązanie
Wzór danej funkcji homograficznej możemy zapisać w postaci
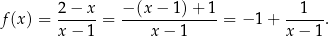
Jej wykresem jest więc hiperbola 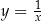 przesunięta o wektor
przesunięta o wektor ![[1,− 1]](https://img.zadania.info/zad/5391420/HzadR2x.png) (czyli asymptotami są proste
(czyli asymptotami są proste 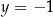 i
i 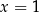 ). Dany okrąg to okrąg ośrodku
). Dany okrąg to okrąg ośrodku 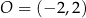 i promieniu
i promieniu 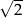 . Szkicujemy teraz tę sytuację.
. Szkicujemy teraz tę sytuację.
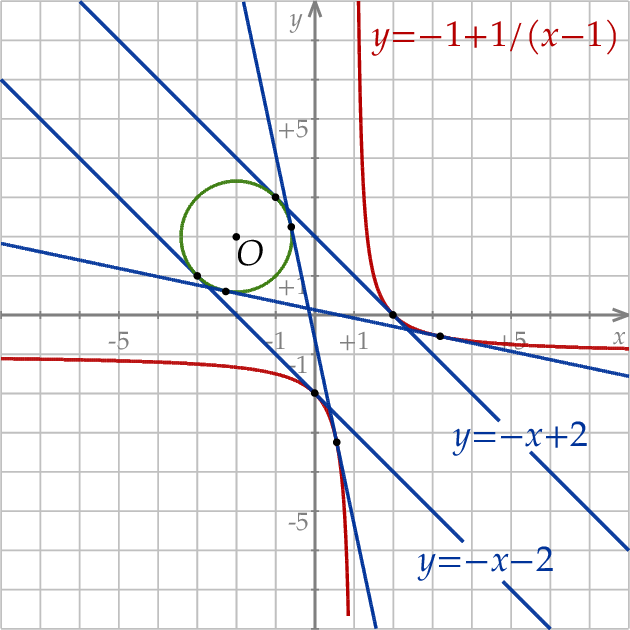
Wyznaczmy najpierw ogólną postać stycznej do danej hiperboli w punkcie
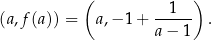
Liczymy pochodną
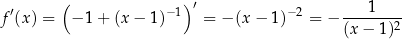
styczna do wykresu funkcji 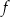 w punkcie
w punkcie 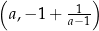 ma więc współczynnik kierunkowy równy
ma więc współczynnik kierunkowy równy 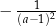 , czyli jest postaci
, czyli jest postaci
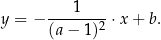
Współczynnik 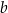 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 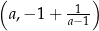 .
.
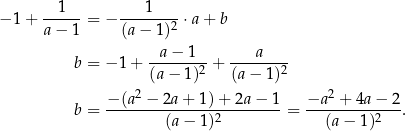
Styczna ma więc postać
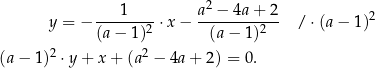
Jeżeli styczna ta ma być styczna do danego okręgu o środku 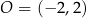 i promieniu
i promieniu 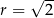 , to środek okręgu
, to środek okręgu 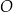 musi być odległy od tej prostej o
musi być odległy od tej prostej o 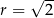 . Korzystamy ze wzoru na odległość punktu
. Korzystamy ze wzoru na odległość punktu 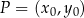 od prostej
od prostej 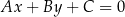 :
:
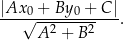
W naszej sytuacji mamy więc równanie
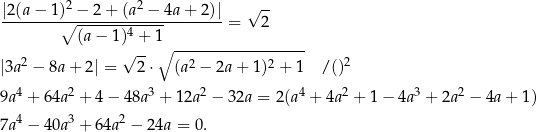
Mamy stąd pierwsze rozwiązanie: 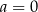 . Jeżeli natomiast
. Jeżeli natomiast 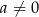 , to mamy równanie
, to mamy równanie
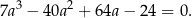
Szukamy jego pierwiastków całkowitych wśród dzielników wyrazu wolnego. Łatwo sprawdzić, że jednym z pierwiastków jest 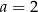
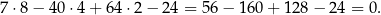
Dzielimy teraz wielomian z lewej strony równania przez 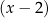 .
.
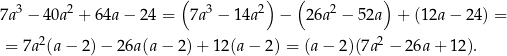
Wyznaczamy teraz pierwiastki trójmianu w drugim nawiasie.
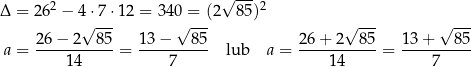
W obu przypadkach 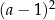 jest liczbą niewymierną, więc współczynniki kierunkowe odpowiednich stycznych też będą niewymierne. W takim razie pozostają nam tylko odpowiedzi
jest liczbą niewymierną, więc współczynniki kierunkowe odpowiednich stycznych też będą niewymierne. W takim razie pozostają nam tylko odpowiedzi 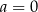 i
i 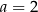 . Odpowiednie styczne mają wtedy równania
. Odpowiednie styczne mają wtedy równania
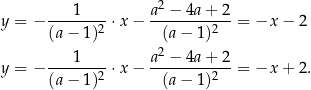
Odpowiedź: 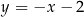 ,
,