Wyznacz liczbę  tak, aby liczby dodatnie
tak, aby liczby dodatnie 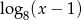 ,
, 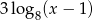 , 6 tworzyły ciąg geometryczny (w podanej kolejności).
, 6 tworzyły ciąg geometryczny (w podanej kolejności).
/Szkoła średnia/Ciągi
Dany jest rosnący ciąg geometryczny 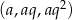 , którego wszystkie wyrazy i iloraz są liczbami całkowitymi nieparzystymi. Jeśli największy wyraz ciągu zmniejszymy o 4, to otrzymamy ciąg arytmetyczny. Oblicz wyraz
, którego wszystkie wyrazy i iloraz są liczbami całkowitymi nieparzystymi. Jeśli największy wyraz ciągu zmniejszymy o 4, to otrzymamy ciąg arytmetyczny. Oblicz wyraz 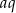 tego ciągu.
tego ciągu.
Dany jest malejący ciąg geometryczny 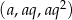 , którego wszystkie wyrazy i iloraz są liczbami całkowitymi niepodzielnymi przez 3. Jeśli najmniejszy wyraz ciągu zwiększymy o 18, to otrzymamy ciąg arytmetyczny. Oblicz wyraz
, którego wszystkie wyrazy i iloraz są liczbami całkowitymi niepodzielnymi przez 3. Jeśli najmniejszy wyraz ciągu zwiększymy o 18, to otrzymamy ciąg arytmetyczny. Oblicz wyraz 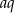 tego ciągu.
tego ciągu.
Ciąg 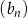 jest nieskończonym ciągiem liczb dodatnich, a ciąg
jest nieskończonym ciągiem liczb dodatnich, a ciąg 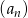 spełnia warunek
spełnia warunek
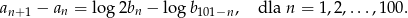
Oblicz 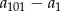 .
.
Liczba przekątnych wielokąta wypukłego, w którym jest  boków i
boków i 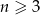 wyraża się wzorem
wyraża się wzorem 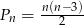 .
.
- Oblicz liczbę przekątnych w dwudziestokącie wypukłym.
- Oblicz, ile boków ma wielokąt wypukły, w którym liczba przekątnych jest pięć razy większa od liczby boków.
- Sprawdź, czy jest prawdziwe następujące stwierdzenie: Każdy wielokąt wypukły o parzystej liczbie boków ma parzystą liczbę przekątnych. Odpowiedź uzasadnij.
- Uzasadnij, że jeżeli liczba boków wielokąta wypukłego jest nieparzysta, to liczba jego przekątnych jest wielokrotnością liczby jego boków.
Dziewiąty wyraz ciągu arytmetycznego 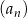 , określonego dla
, określonego dla 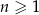 , jest równy 34, a suma jego ośmiu początkowych wyrazów jest równa 110. Oblicz pierwszy wyraz i różnicę tego ciągu.
, jest równy 34, a suma jego ośmiu początkowych wyrazów jest równa 110. Oblicz pierwszy wyraz i różnicę tego ciągu.
Jedenasty wyraz ciągu arytmetycznego 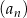 , określonego dla
, określonego dla 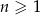 , jest równy
, jest równy 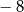 , a suma jego dziesięciu początkowych wyrazów jest równa
, a suma jego dziesięciu początkowych wyrazów jest równa 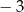 . Oblicz pierwszy wyraz i różnicę tego ciągu.
. Oblicz pierwszy wyraz i różnicę tego ciągu.
Suma ośmiu początkowych wyrazów ciągu arytmetycznego 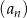 , określonego dla
, określonego dla 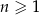 , jest równa 90, a suma
, jest równa 90, a suma 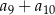 jest równa 57,5. Oblicz pierwszy wyraz i różnicę tego ciągu.
jest równa 57,5. Oblicz pierwszy wyraz i różnicę tego ciągu.
Ciąg 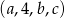 jest arytmetyczny, a ciąg
jest arytmetyczny, a ciąg 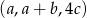 jest geometryczny. Oblicz
jest geometryczny. Oblicz 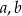 i
i  .
.
Wyznacz cztery początkowe wyrazy ciągu geometrycznego, jeśli: 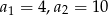 .
.
Dany jest ciąg 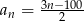 .
.
- Oblicz piętnasty wyraz tego ciągu.
- Którym wyrazem tego ciągu jest liczba 10.
- Ile wyrazów ujemnych ma ten ciąg?
Dany jest ciąg 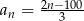 .
.
- Oblicz osiemnasty wyraz tego ciągu.
- Którym wyrazem tego ciągu jest liczba 20.
- Ile wyrazów ujemnych ma ten ciąg?
W trójkąt równoboczny o boku długości  wpisano koło, w które następnie wpisano trójkąt równoboczny, a w ten trójkąt znów koło i tak dalej. Oblicz sumę pól wszystkich wpisanych kół.
wpisano koło, w które następnie wpisano trójkąt równoboczny, a w ten trójkąt znów koło i tak dalej. Oblicz sumę pól wszystkich wpisanych kół.
W trójkąt równoboczny o boku długości 3 wpisano koło, w które następnie wpisano trójkąt równoboczny, a w ten trójkąt znów koło i tak dalej. Oblicz sumę pól wszystkich wpisanych kół.
Wyznacz wszystkie ciągi geometryczne o wyrazach różnych od zera, w których każdy wyraz, rozpoczynając od wyrazu trzeciego, jest równy średniej arytmetycznej dwóch poprzednich wyrazów.
Oblicz granicę 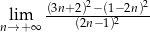 .
.
Oblicz granicę 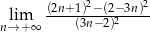 .
.
Pięćdziesiąty wyraz ciągu arytmetycznego 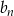 jest równy 5. Oblicz
jest równy 5. Oblicz 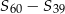 , gdzie
, gdzie 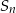 oznacza sumę
oznacza sumę  początkowych wyrazów ciągu
początkowych wyrazów ciągu 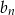 .
.
Ciąg 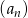 , gdzie
, gdzie 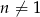 jest ciągiem arytmetycznym w którym
jest ciągiem arytmetycznym w którym 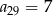 . Oblicz
. Oblicz 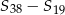 , gdzie
, gdzie 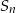 oznacza sumę
oznacza sumę  początkowych wyrazów ciągu
początkowych wyrazów ciągu 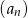 .
.
Jednym z pierwiastków trójmianu kwadratowego 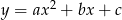 jest
jest 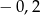 . Liczby
. Liczby 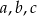 tworzą w podanej kolejności ciąg arytmetyczny, a ich suma wynosi 24. Oblicz drugi pierwiastek tego trójmianu.
tworzą w podanej kolejności ciąg arytmetyczny, a ich suma wynosi 24. Oblicz drugi pierwiastek tego trójmianu.
Jedno z rozwiązań równania 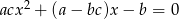 z niewiadomą
z niewiadomą  jest równe 4. Liczby
jest równe 4. Liczby 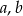 i
i  (w podanej kolejności) tworzą ciąg arytmetyczny, w którym pierwszy wyraz jest o 6 większy od trzeciego. Znajdź drugie rozwiązanie tego równania.
(w podanej kolejności) tworzą ciąg arytmetyczny, w którym pierwszy wyraz jest o 6 większy od trzeciego. Znajdź drugie rozwiązanie tego równania.
Liczby 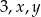 są kolejnymi wyrazami ciągu arytmetycznego. Jeśli liczbę
są kolejnymi wyrazami ciągu arytmetycznego. Jeśli liczbę  zmniejszymy o 5, a liczbę
zmniejszymy o 5, a liczbę 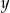 zwiększymy o 17, to otrzymane liczby będą kolejnymi wyrazami ciągu geometrycznego. Wyznacz wartości liczbowe
zwiększymy o 17, to otrzymane liczby będą kolejnymi wyrazami ciągu geometrycznego. Wyznacz wartości liczbowe  i
i 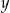 .
.
Liczby 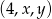 są kolejnymi wyrazami ciągu arytmetycznego. Jeśli liczbę
są kolejnymi wyrazami ciągu arytmetycznego. Jeśli liczbę  zwiększymy o 1, a liczbę
zwiększymy o 1, a liczbę 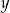 zwiększymy o 3, to otrzymane liczby będą kolejnymi wyrazami ciągu geometrycznego. Wyznacz
zwiększymy o 3, to otrzymane liczby będą kolejnymi wyrazami ciągu geometrycznego. Wyznacz  i
i 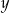 .
.
Wyznacz pierwsze trzy wyrazy ciągu geometrycznego wiedząc, że są one dodatnie, ich suma jest równa 21 oraz suma ich odwrotności jest równa 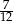 .
.
Wyznacz pierwsze trzy wyrazy ciągu geometrycznego wiedząc, że są one dodatnie, ich suma jest równa 28 oraz suma ich odwrotności jest równa 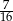 .
.
Ciąg 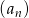 jest określony wzorem
jest określony wzorem 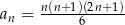 dla
dla 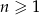 . Wykaż, że każdy kolejny wyraz tego ciągu jest większy od poprzedniego wyrazu o kwadrat liczby naturalnej.
. Wykaż, że każdy kolejny wyraz tego ciągu jest większy od poprzedniego wyrazu o kwadrat liczby naturalnej.
W ciągu arytmetycznym 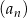 , określonym dla
, określonym dla 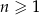 , dane są wyrazy:
, dane są wyrazy: 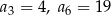 . Wyznacz wszystkie wartości
. Wyznacz wszystkie wartości  , dla których wyrazy ciągu
, dla których wyrazy ciągu 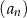 są mniejsze od 200.
są mniejsze od 200.
W ciągu arytmetycznym 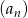 dane są wyrazy:
dane są wyrazy: 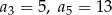 . Oblicz, ile wyrazów ciągu
. Oblicz, ile wyrazów ciągu 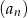 jest mniejszych niż 83.
jest mniejszych niż 83.
Wykaż, że jeżeli liczby 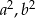 i
i 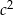 tworzą ciąg arytmetyczny, który nie jest stały, to liczby
tworzą ciąg arytmetyczny, który nie jest stały, to liczby 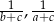 i
i 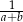 również tworzą ciąg arytmetyczny.
również tworzą ciąg arytmetyczny.
Liczby 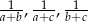 , gdzie
, gdzie 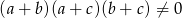 są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że liczby
są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że liczby 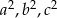 są również wyrazami ciągu arytmetycznego.
są również wyrazami ciągu arytmetycznego.
Ile wyrazów ciągu o wyrazie ogólnym 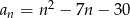 , dla
, dla 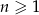 , jest liczbami ujemnymi?
, jest liczbami ujemnymi?
Ile wyrazów ujemnych ma ciąg 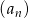 określony wzorem
określony wzorem 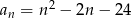 dla
dla 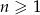 ?
?
Ile wyrazów ujemnych ma ciąg 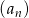 określony wzorem
określony wzorem 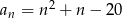 dla
dla 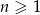 ?
?
Ile wyrazów ciągu o wyrazie ogólnym 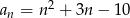 , dla
, dla 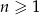 , jest liczbami ujemnymi?
, jest liczbami ujemnymi?

