Podstawą ostrosłupa 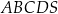 jest kwadrat
jest kwadrat  (patrz rysunek).
(patrz rysunek).
Krawędź 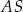 jest wysokością tego ostrosłupa. Odległość punktu
jest wysokością tego ostrosłupa. Odległość punktu 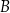 od krawędzi
od krawędzi 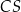 jest równa
jest równa 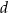 , a kąt dwuścienny między ścianami
, a kąt dwuścienny między ścianami 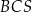 i
i 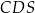 ma miarę
ma miarę 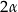 , gdzie
, gdzie 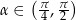 . Oblicz:
. Oblicz:
-
odległość punktu
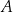 od krawędzi
od krawędzi 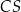
-
wysokość tego ostrosłupa.

 podstawa
podstawa  jest trójkątem prostokątnym,
jest trójkątem prostokątnym, 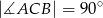 . Sinus jednego z kątów ostrych podstawy jest równy 0,6 . Promień okręgu opisanego na podstawie ma długość 10 cm. Wysokość
. Sinus jednego z kątów ostrych podstawy jest równy 0,6 . Promień okręgu opisanego na podstawie ma długość 10 cm. Wysokość 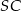 ostrosłupa ma długość 24 cm. Oblicz:
ostrosłupa ma długość 24 cm. Oblicz: 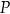 krawędzi bocznej
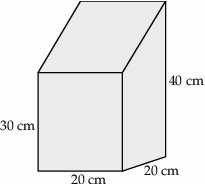
krawędzi bocznej 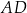 graniastosłupa prawidłowego trójkątnego
graniastosłupa prawidłowego trójkątnego 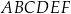 o krawędzi podstawy równej
o krawędzi podstawy równej  poprowadzono dwie płaszczyzny. Jedna przechodzi przez przeciwległą krawędź dolnej podstawy i jest nachylona do tej podstawy pod kątem
poprowadzono dwie płaszczyzny. Jedna przechodzi przez przeciwległą krawędź dolnej podstawy i jest nachylona do tej podstawy pod kątem  , a druga przechodzi przez przeciwległą krawędź górnej podstawy i jest nachylona do tej podstawy pod kątem
, a druga przechodzi przez przeciwległą krawędź górnej podstawy i jest nachylona do tej podstawy pod kątem 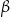 (zobacz rysunek).
(zobacz rysunek). 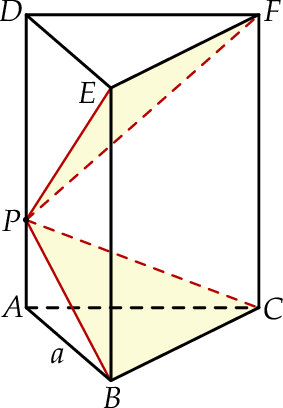
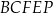 jest równa
jest równa 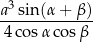
 . Pole podstawy jest równe sumie pól dwóch przystających ścian bocznych graniastosłupa. Jakie powinny być długości pozostałych krawędzi graniastosłupa, aby jego objętość była największa?
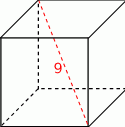
. Pole podstawy jest równe sumie pól dwóch przystających ścian bocznych graniastosłupa. Jakie powinny być długości pozostałych krawędzi graniastosłupa, aby jego objętość była największa? 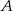 do wierzchołka będącego drugim końcem przekątnej sześcianu wychodzącej z wierzchołka
do wierzchołka będącego drugim końcem przekątnej sześcianu wychodzącej z wierzchołka  , przy czym była to droga najkrótsza. Narysuj siatkę sześcianu i oblicz odległość, jaką pokonała mrówka, jeżeli krawędź sześcianu ma długość
, przy czym była to droga najkrótsza. Narysuj siatkę sześcianu i oblicz odległość, jaką pokonała mrówka, jeżeli krawędź sześcianu ma długość 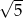 .
. 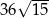 .
.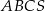 jest trójkąt równoboczny
jest trójkąt równoboczny 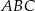 o boku długości 6. Na krawędziach bocznych
o boku długości 6. Na krawędziach bocznych 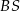 i
i 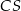 wybrano punkty, odpowiednio
wybrano punkty, odpowiednio 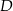 i
i 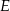 , takie że
, takie że 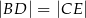 oraz
oraz 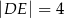 (zobacz rysunek). Płaszczyzna
(zobacz rysunek). Płaszczyzna 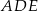 jest prostopadła do płaszczyzny ściany bocznej
jest prostopadła do płaszczyzny ściany bocznej 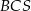 ostrosłupa.
ostrosłupa. 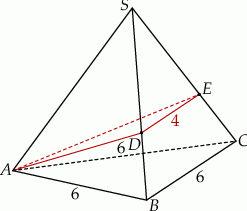
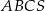 jest trójkąt równoboczny
jest trójkąt równoboczny 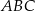 o boku długości 8. Na krawędziach bocznych
o boku długości 8. Na krawędziach bocznych 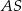 i
i 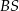 wybrano punkty, odpowiednio
wybrano punkty, odpowiednio 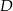 i
i 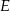 , takie że
, takie że 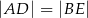 oraz
oraz 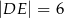 (zobacz rysunek). Płaszczyzna
(zobacz rysunek). Płaszczyzna 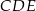 jest prostopadła do płaszczyzny ściany bocznej
jest prostopadła do płaszczyzny ściany bocznej 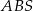 ostrosłupa.
ostrosłupa. 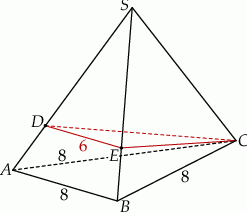
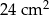 . Każda krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem
. Każda krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 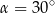 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa. 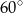 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa. 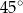 .
. 
 . Kąt między krawędzią boczną i krawędzią podstawy ma miarę
. Kąt między krawędzią boczną i krawędzią podstawy ma miarę 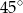 . Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej jej krawędzi bocznej. Sporządź rysunek ostrosłupa i zaznacz otrzymany przekrój. Oblicz pole tego przekroju.
. Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej jej krawędzi bocznej. Sporządź rysunek ostrosłupa i zaznacz otrzymany przekrój. Oblicz pole tego przekroju.  . Kąt między krawędzią boczną i krawędzią podstawy ma miarę
. Kąt między krawędzią boczną i krawędzią podstawy ma miarę 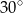 . Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej jej krawędzi bocznej. Sporządź rysunek ostrosłupa i zaznacz otrzymany przekrój. Oblicz pole tego przekroju.
. Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej jej krawędzi bocznej. Sporządź rysunek ostrosłupa i zaznacz otrzymany przekrój. Oblicz pole tego przekroju. 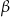 . Wszystkie krawędzie boczne mają długość
. Wszystkie krawędzie boczne mają długość 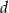 i są nachylone do płaszczyzny podstawy pod kątem o mierze
i są nachylone do płaszczyzny podstawy pod kątem o mierze  . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 