Suma reszt jakie otrzymujemy dzieląc wielomian 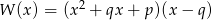 przez dwumiany
przez dwumiany 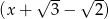 i
i 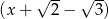 jest równa
jest równa 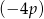 , gdzie
, gdzie 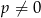 . Oblicz
. Oblicz 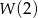 .
.
/Szkoła średnia/Funkcje/Wielomiany
Wielomian 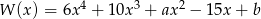 jest podzielny przez trójmian
jest podzielny przez trójmian 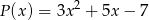 . Wyznacz liczby
. Wyznacz liczby  i
i 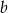 .
.
Dany jest wielomian 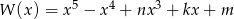 . Wyznacz wszystkie wartości parametrów
. Wyznacz wszystkie wartości parametrów 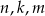 dla których reszta z dzielenia wielomianu
dla których reszta z dzielenia wielomianu 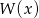 przez wielomian
przez wielomian 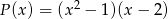 jest równa
jest równa 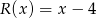 .
.
Oblicz największą wartość wielomianu 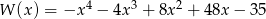 .
.
Pierwiastkami wielomianu stopnia trzeciego są liczby 1, 3, 5. Współczynnik przy najwyższej potędze zmiennej tego wielomianu jest równy 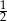 . Uzasadnij, że dla każdej liczby całkowitej nieparzystej wartość tego wielomianu jest liczbą podzielną przez 24.
. Uzasadnij, że dla każdej liczby całkowitej nieparzystej wartość tego wielomianu jest liczbą podzielną przez 24.
Dla jakich wartości 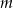 reszta z dzielenia wielomianu
reszta z dzielenia wielomianu 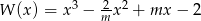 przez dwumian
przez dwumian 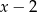 jest mniejsza lub równa 6?
jest mniejsza lub równa 6?
Dla jakich wartości 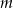 reszta z dzielenia wielomianu
reszta z dzielenia wielomianu 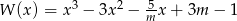 przez dwumian
przez dwumian 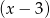 jest niewiększa od 3?
jest niewiększa od 3?
Wielomian 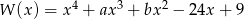 jest kwadratem wielomianu
jest kwadratem wielomianu 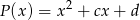 . Oblicz
. Oblicz  oraz
oraz 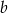 .
.
Przedstaw wielomian 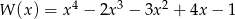 w postaci iloczynu dwóch wielomianów stopnia drugiego o współczynnikach całkowitych i takich, że współczynniki przy drugich potęgach są równe jeden.
w postaci iloczynu dwóch wielomianów stopnia drugiego o współczynnikach całkowitych i takich, że współczynniki przy drugich potęgach są równe jeden.
Dany jest wielomian 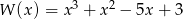 .
.
- Oblicz resztę z dzielenia tego wielomianu przez dwumian
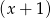 .
. - Oblicz miejsca zerowe tego wielomianu.
- Rozwiąż nierówność
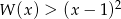 .
.
Nie wykonując dzielenia, wyznacz resztę z dzielenia wielomianu 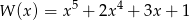 przez
przez 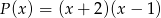 .
.
Dana jest funkcja 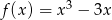 dla
dla 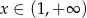 . Zbadaj na podstawie definicji monotoniczność tej funkcji w przedziale
. Zbadaj na podstawie definicji monotoniczność tej funkcji w przedziale 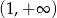 .
.
Wyznacz maksymalne przedziały monotoniczności funkcji 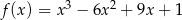 .
.
Wyznacz przedziały monotoniczności funkcji 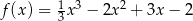 .
.
Wyznacz maksymalne przedziały monotoniczności funkcji 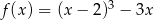 .
.
Dla jakiej wartości parametru 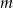 wielomian
wielomian 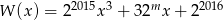 jest podzielny przez dwumian
jest podzielny przez dwumian 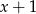 .
.
Wielomian 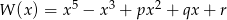 jest podzielny przez wielomian
jest podzielny przez wielomian 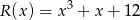 . Wyznacz liczby
. Wyznacz liczby 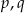 i
i  .
.
Reszta z dzielenia wielomianu 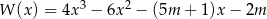 przez dwumian
przez dwumian 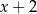 jest równa
jest równa 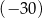 . Oblicz
. Oblicz 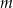 i dla wyznaczonej wartości
i dla wyznaczonej wartości 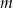 rozwiąż nierówność
rozwiąż nierówność 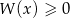 .
.
Wyznacz najmniejszą 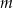 i największą
i największą 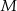 wartość funkcji
wartość funkcji 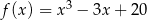 w przedziale
w przedziale 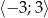 .
.
Dane są wielomiany 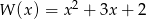 ,
, 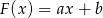 ,
, 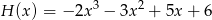 . Wyznacz współczynniki
. Wyznacz współczynniki 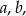 dla których wielomiany
dla których wielomiany 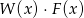 oraz
oraz 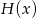 są równe.
są równe.
Dane są wielomiany 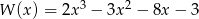 i
i 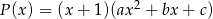 .
.
- Wyznacz współczynniki
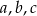 tak, aby
tak, aby 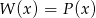 .
. - Przedstaw wielomian
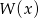 jako iloczyn wielomianów liniowych.
jako iloczyn wielomianów liniowych.
Dany jest wielomian 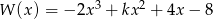 .
.
- Wyznacz wartość
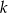 tak, aby reszta z dzielenia wielomianu W przez dwumian
tak, aby reszta z dzielenia wielomianu W przez dwumian 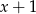 była równa -6.
była równa -6. - Dla znalezionej wartości
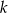 rozłóż wielomian na czynniki liniowe.
rozłóż wielomian na czynniki liniowe. - Dla znalezionej wartości
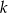 rozwiąż nierówność
rozwiąż nierówność 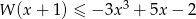 .
.
Reszta z dzielenia wielomianu 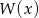 przez wielomian
przez wielomian 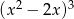 jest równa
jest równa 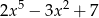 . Oblicz resztę z dzielenia wielomianu
. Oblicz resztę z dzielenia wielomianu 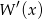 przez dwumian
przez dwumian 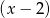 .
.

