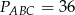Zadanie nr 1296836
Prosta o równaniu 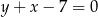 zawiera jedną z dwusiecznych kątów wewnętrznych trójkąta
zawiera jedną z dwusiecznych kątów wewnętrznych trójkąta 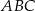 , w którym
, w którym 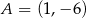 i
i  . Oblicz pole tego trójkąta.
. Oblicz pole tego trójkąta.
Rozwiązanie
Sprawdzamy najpierw, że żaden z podanych punktów nie leży na podanej dwusiecznej – jest to więc dwusieczna kąta przy wierzchołku 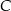 . Szkicujemy teraz opisaną sytuację.
. Szkicujemy teraz opisaną sytuację.
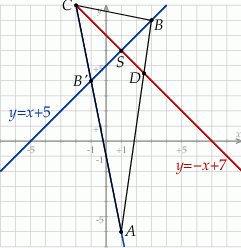
Pole trójkąta  będzie łatwe do obliczenia, jeżeli będziemy znali współrzędne jego trzeciego wierzchołka
będzie łatwe do obliczenia, jeżeli będziemy znali współrzędne jego trzeciego wierzchołka 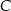 . Obliczymy te współrzędne na dwa sposoby.
. Obliczymy te współrzędne na dwa sposoby.
Sposób I
Dwusieczna kąta jest jego osią symetrii, więc jeżeli odbijemy prostą 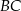 względem podanej dwusiecznej, to otrzymamy prostą
względem podanej dwusiecznej, to otrzymamy prostą 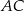 . Ta obserwacja pozwala napisać równanie prostej
. Ta obserwacja pozwala napisać równanie prostej 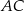 – jest to prosta przechodząca przez punkt
– jest to prosta przechodząca przez punkt 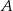 i punkt
i punkt 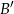 będący obrazem punktu
będący obrazem punktu 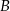 w symetrii względem dwusiecznej
w symetrii względem dwusiecznej 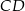 . Aby wyznaczyć obraz
. Aby wyznaczyć obraz 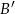 punktu
punktu 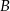 w tej symetrii piszemy najpierw równanie prostej prostopadłej do dwusiecznej i przechodzącej przez punkt
w tej symetrii piszemy najpierw równanie prostej prostopadłej do dwusiecznej i przechodzącej przez punkt 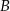 . Jest to prosta postaci
. Jest to prosta postaci 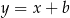 . Współczynnik
. Współczynnik 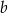 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 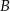 .
.
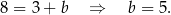
Prosta 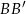 ma więc równanie
ma więc równanie 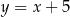 . Wyznaczmy jej punkt wspólny
. Wyznaczmy jej punkt wspólny  z dwusieczną
z dwusieczną  .
.
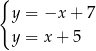
Dodajemy równania układu stronami i mamy
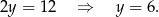
Stąd
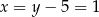
i 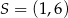 . Punkt
. Punkt 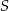 jest środkiem odcinka
jest środkiem odcinka 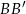 , więc
, więc
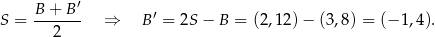
Teraz możemy napisać równanie prostej 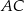 , czyli prostej
, czyli prostej 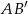 . Szukamy prostej w postaci
. Szukamy prostej w postaci 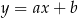 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 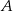 i
i 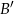 .
.
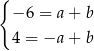
Dodajemy równania układu stronami i mamy
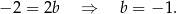
Stąd 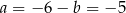 i prosta
i prosta 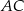 ma równanie
ma równanie 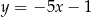 . Szukamy teraz punktu
. Szukamy teraz punktu 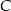 wspólnego danej dwusiecznej i prostej
wspólnego danej dwusiecznej i prostej 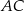 .
.
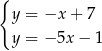
Odejmujemy od pierwszego równania drugie i mamy
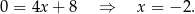
Stąd 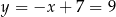 i
i 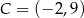 . Pozostało obliczyć pole trójkąta
. Pozostało obliczyć pole trójkąta 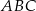 . Korzystamy ze wzoru
. Korzystamy ze wzoru
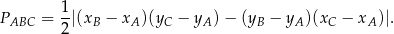
Mamy zatem
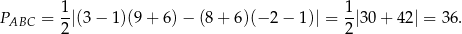
Sposób II
Tym razem zacznijmy od wyznaczenia równania prostej 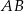 . Szukamy prostej w postaci
. Szukamy prostej w postaci 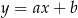 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 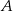 i
i 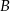 .
.
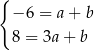
Odejmujemy od drugiego równania pierwsze i mamy
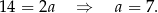
Stąd 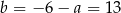 i prosta
i prosta 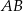 ma równanie
ma równanie 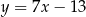 . Wyznaczmy teraz jej punkt wspólny
. Wyznaczmy teraz jej punkt wspólny  z daną dwusieczną.
z daną dwusieczną.
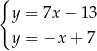
Odejmujemy od pierwszego równania drugie i mamy
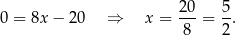
Stąd
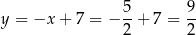
i 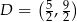 Korzystamy teraz z twierdzenia o dwusiecznej
Korzystamy teraz z twierdzenia o dwusiecznej
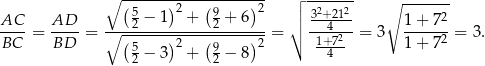
Ta informacja pozwoli nam wyznaczyć współrzędne punktu 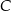 . Wiemy, że leży on na danej dwusiecznej, więc ma współrzędne postaci
. Wiemy, że leży on na danej dwusiecznej, więc ma współrzędne postaci 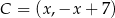 . Ponadto
. Ponadto
![AC 2 = 9BC 2 [ ] (x− 1)2 + (−x + 7 + 6 )2 = 9 (x − 3 )2 + (−x + 7 − 8)2 [ ] (x − 1 )2 + (−x + 13 )2 = 9 (x − 3 )2 + (−x − 1)2 x2 − 2x+ 1+ x2 − 26x + 169 = 9(x2 − 6x + 9 + x2 + 2x + 1) 2 0 = 16x − 8x − 80 / : 8 0 = 2x2 − x − 10.](https://img.zadania.info/zad/1296836/HzadR65x.gif)
Rozwiązujemy otrzymane równanie kwadratowe
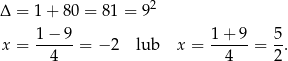
Drugie rozwiązanie da nam współrzędne punktu 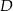 , więc
, więc 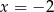 i
i
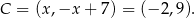
Pole trójkąta możemy obliczyć tak jak w poprzednim sposobie, ale możemy też zrobić to bardziej bezpośrednio – ze wzoru na odległość od prostej. Wysokość  trójkąta
trójkąta  opuszczona na podstawę
opuszczona na podstawę 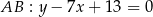 jest równa
jest równa
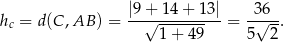
Obliczmy jeszcze długość podstawy 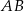
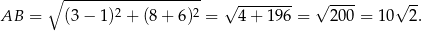
Pole trójkąta 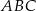 jest więc równe
jest więc równe
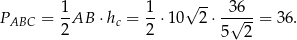
Odpowiedź: