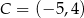/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt

Zadanie nr 1965876

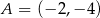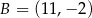Punkty A = (− 2,− 4) i B = (11,− 2) są wierzchołkami trójkąta 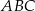ABC . Wierzchołek 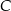C tego trójkąta leży na prostej 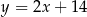y = 2x + 14 , a dwusieczna kąta 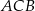ACB przecina bok 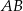AB w punkcie 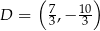( ) D = 7 ,− 10 3 3 . Oblicz współrzędne wierzchołka 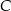C trójkąta ABC .

Wersja PDF

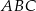Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

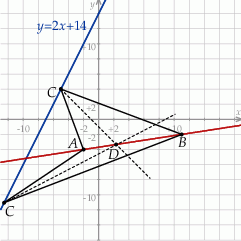
Zastanówmy się jak wyznaczyć współrzędne wierzchołka 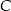C . Wiemy, że leży on na prostej 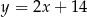y = 2x + 1 4 , więc ma współrzędne postaci 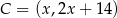C = (x,2x + 1 4) . Ponadto, na mocy twierdzenia o dwusiecznej,

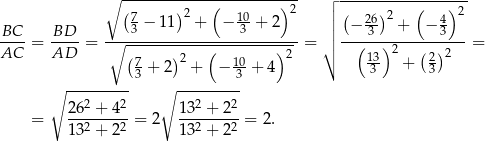
∘ ------------------------- ┌ ------------------ ( )2 ( ) 2 │ ( )2 ( ) 2 BC BD 73 − 11 + − 103 + 2 ││ − 236 + − 43 ----= ----= -∘-------------------------= │∘ --(--)-2----------= AC AD (7 )2 ( 10 )2 13 + ( 2)2 3 + 2 + − 3 + 4 3 3 ∘ --------- ∘ --------- 262-+-42- 13-2 +-22 = 132 + 22 = 2 13 2 + 22 = 2.

Mamy w takim razie równanie

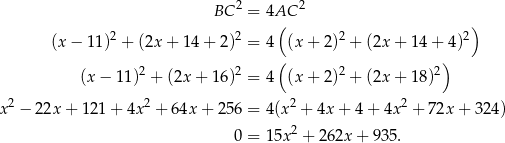
2 2 BC = 4AC 2 2 ( 2 2) (x − 11) + (2x + 1 4+ 2 ) = 4 (x+ 2) + (2x+ 14+ 4) 2 2 ( 2 2) (x − 11) + (2x + 16 ) = 4 (x+ 2) + (2x+ 18) 2 2 2 2 x − 22x + 1 21+ 4x + 64x + 256 = 4(x + 4x + 4 + 4x + 72x + 3 24) 0 = 15x2 + 262x + 935.

Rozwiązujemy otrzymane równanie kwadratowe

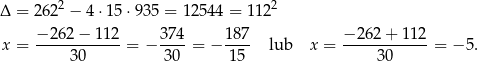
2 2 Δ = 262 − 4 ⋅15⋅ 935 = 12 544 = 112 −-262-−-112- 374- 187- −-26-2+-1-12 x = 30 = − 30 = − 15 lub x = 30 = − 5.

Mamy wtedy

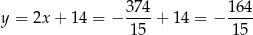
374 164 y = 2x + 14 = − ----+ 14 = − ---- 15 15

i

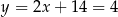
y = 2x + 1 4 = 4

odpowiednio. Są więc dwa punkty spełniające warunki zadania: 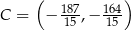( ) C = − 18175 ,− 16145 lub C = (− 5,4) .  
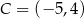Odpowiedź: 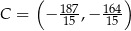( ) C = − 18175 ,− 16145 lub C = (− 5,4)

Wersja PDF