Dany jest trapez prostokątny  o podstawach
o podstawach  i
i  , w którym boki
, w którym boki 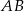 i
i 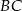 są prostopadłe. Dwusieczne kątów
są prostopadłe. Dwusieczne kątów 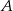 i
i 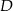 przecinają się w punkcie
przecinają się w punkcie 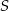 leżącym na boku
leżącym na boku 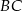 . Wykaż, że
. Wykaż, że 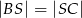 .
.
/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez
Ramię trapezu równoramiennego 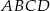 ma długość
ma długość 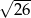 . Przekątne w tym trapezie są prostopadłe, a punkt ich przecięcia dzieli je w stosunku 2:3. Oblicz pole tego trapezu.
. Przekątne w tym trapezie są prostopadłe, a punkt ich przecięcia dzieli je w stosunku 2:3. Oblicz pole tego trapezu.
Długość ramienia trapezu jest równa 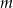 , a odległość od niego środka przeciwległego ramienia jest równa
, a odległość od niego środka przeciwległego ramienia jest równa 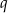 . Wyznacz pole trapezu.
. Wyznacz pole trapezu.
W kole o promieniu 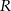 poprowadzono średnicę
poprowadzono średnicę 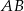 i równoległą do niej cięciwę
i równoległą do niej cięciwę 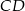 . Oblicz pole powstałego trapezu
. Oblicz pole powstałego trapezu 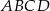 , jeżeli kąt ostry tego trapezu ma miarę
, jeżeli kąt ostry tego trapezu ma miarę  .
.
Różnica kwadratów długości przekątnych trapezu prostokątnego wynosi 21, jego wysokość ma długość 4, a dłuższe ramię ma długość 5. Oblicz pole trapezu.
W trapez prostokątny można wpisać okrąg. Jedna z jego podstaw ma długość  , druga jest trzy razy dłuższa. Oblicz pole trapezu oraz długość odcinka łączącego środki ramion trapezu.
, druga jest trzy razy dłuższa. Oblicz pole trapezu oraz długość odcinka łączącego środki ramion trapezu.
Przekątne trapezu 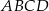 przecinają się w punkcie
przecinają się w punkcie 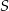 , jego podstawy mają długości
, jego podstawy mają długości 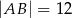 i
i 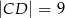 , a wysokość trapezu ma długość 8. Punkt
, a wysokość trapezu ma długość 8. Punkt 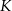 jest środkiem odcinka
jest środkiem odcinka 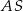 (zobacz rysunek).
(zobacz rysunek).
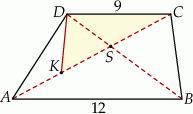
Oblicz pole trójkąta 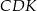 .
.
Krótsza podstawa trapezu ma długość 2, a ramiona długości 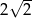 i 4 tworzą z dłuższą podstawą kąty o miarach
i 4 tworzą z dłuższą podstawą kąty o miarach 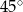 i
i 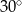 . Oblicz pole trapezu.
. Oblicz pole trapezu.
Krótsza podstawa trapezu ma długość 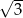 , a ramiona długości
, a ramiona długości 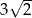 i 6 tworzą z dłuższą podstawą kąty o miarach
i 6 tworzą z dłuższą podstawą kąty o miarach 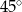 i
i 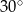 odpowiednio. Oblicz pole trapezu.
odpowiednio. Oblicz pole trapezu.
Dany jest trapez prostokątny (zobacz rysunek).
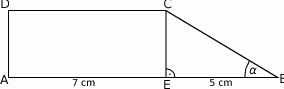
Wyznacz obwód tego trapezu, jeżeli miara kąta przy wierzchołku 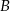 wynosi
wynosi 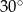 .
.
Wykaż, że w dowolnym trapezie suma długości podstaw jest mniejsza od sumy długości przekątnych.
Wykaż, że w dowolnym trapezie suma długości ramion jest mniejsza od sumy długości przekątnych.
Wysokość trapezu równoramiennego ma długość 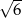 , a jedna z podstaw jest trzy razy dłuższa od drugiej. Oblicz pole trapezu wiedząc, że sinus jego kąta ostrego jest równy 0,2.
, a jedna z podstaw jest trzy razy dłuższa od drugiej. Oblicz pole trapezu wiedząc, że sinus jego kąta ostrego jest równy 0,2.
Wykaż, że jeśli przekątna trapezu równoramiennego zawiera się w dwusiecznej jego kąta ostrego, to ramię jest równe krótszej podstawie.
Obwód trapezu równoramiennego wynosi 32 cm. Wysokość poprowadzona z wierzchołka kąta rozwartego dzieli podstawę na dwa odcinki o długościach 3 cm i 11 cm. Oblicz pole trapezu.
Obwód trapezu równoramiennego wynosi 50 cm. Wysokość poprowadzona z wierzchołka kąta rozwartego dzieli podstawę na dwa odcinki o długościach 5 cm i 12 cm. Oblicz pole trapezu.
Przekątne dzielą trapez na cztery trójkąty. Wykaż, że pola tych trójkątów, w których jeden z boków jest ramieniem trapezu, są równe.
Przekątne dzielą trapez na cztery trójkąty. Wykaż, że stosunek pól tych trójkątów, w których jeden z boków jest podstawą trapezu, jest równy stosunkowi kwadratów długości podstaw trapezu.
Przekątne dzielą trapez na cztery trójkąty. Wykaż, że stosunek pól trójkątów takich, że bokiem jednego jest ramię trapezu, a bokiem drugiego jest podstawa trapezu, jest równy stosunkowi długości podstaw trapezu.
Czworokąt 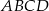 jest trapezem prostokątnym, w którym
jest trapezem prostokątnym, w którym 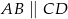 . Wykaż że
. Wykaż że
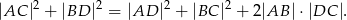
Obwód trapezu równoramiennego opisanego na okręgu jest równy 16, a przekątna trapezu ma długość 5. Oblicz długość promienia okręgu wpisanego w ten trapez i promienia okręgu opisanego na nim.
Przekątne trapezu równoramiennego 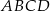 przecinają się w punkcie
przecinają się w punkcie  . Przekątna
. Przekątna  tworzy z dłuższą podstawą
tworzy z dłuższą podstawą 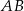 kąt
kąt  i z ramieniem
i z ramieniem 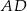 kąt
kąt 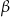 takie, że
takie, że 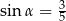 i
i 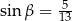 . Pole trapezu
. Pole trapezu 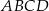 jest równe 448. Oblicz pole trójkąta
jest równe 448. Oblicz pole trójkąta 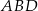 .
.
Stosunek długości ramion trapezu opisanego na okręgu o promieniu 6 cm wynosi 3:4. Obwód trapezu jest równy 70 cm. Oblicz długości podstaw trapezu.
W trapez 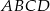 , gdzie
, gdzie 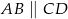 i
i 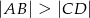 , wpisano okrąg (patrz rysunek).
, wpisano okrąg (patrz rysunek).
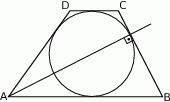
Dwusieczna kąta ostrego przy wierzchołku 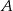 jest prostopadła do ramienia
jest prostopadła do ramienia 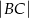 .
.
- Wykaż, że dwusieczna kąta przy wierzchołku
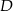 jest równoległa do ramienia
jest równoległa do ramienia 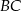 .
. - Oblicz
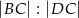 .
.
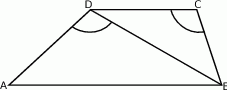
W trapezie 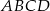 długość podstawy
długość podstawy 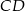 jest równa 18, a długości ramion trapezu
jest równa 18, a długości ramion trapezu 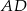 i
i 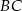 są odpowiednio równe 25 i 15. Kąty
są odpowiednio równe 25 i 15. Kąty  i
i  , zaznaczone na rysunku, mają równe miary. Oblicz obwód tego trapezu.
, zaznaczone na rysunku, mają równe miary. Oblicz obwód tego trapezu.