Wykaż, że iloczyn trzech kolejnych liczb podzielnych przez 3 dzieli się przez 81.
/Szkoła średnia/Liczby/Liczby całkowite
Uzasadnij, że dla dowolnych liczb naturalnych 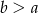 zachodzi równość
zachodzi równość 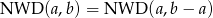 .
.
Wykaż, że jeżeli liczby całkowite 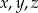 spełniają równanie
spełniają równanie 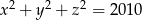 to co najwyżej jedna z liczb
to co najwyżej jedna z liczb 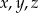 dzieli się przez 4.
dzieli się przez 4.
Udowodnij, że jeżeli liczba całkowita  nie jest podzielna przez 3, to wyrażenie
nie jest podzielna przez 3, to wyrażenie 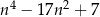 jest podzielne przez 9.
jest podzielne przez 9.
Wykaż, że różnica kwadratów dwóch kolejnych liczb parzystych jest liczbą podzielną przez 4.
Wykaż, że różnica kwadratów dwóch kolejnych liczb nieparzystych jest liczbą podzielną przez 8.
Dany ciąg arytmetyczny 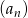 taki, że
taki, że 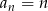 , dla
, dla 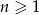 . Udowodnij, że iloczyn każdych dziesięciu kolejnych wyrazów tego ciągu jest podzielny przez
. Udowodnij, że iloczyn każdych dziesięciu kolejnych wyrazów tego ciągu jest podzielny przez 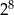 .
.
Wykaż, że liczba 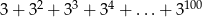 jest podzielna przez 6.
jest podzielna przez 6.
Uzasadnij, że równanie 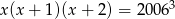 nie ma pierwiastków całkowitych.
nie ma pierwiastków całkowitych.
Wykaż, że suma kwadratów dwóch kolejnych liczb nieparzystych nie dzieli się przez 4.
Udowodnij, że suma kwadratów dwóch kolejnych liczb nieparzystych jest liczbą parzystą.
Wykaż, że jeżeli 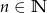 , to liczba postaci
, to liczba postaci 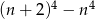 jest podzielna przez 16.
jest podzielna przez 16.
Wykaż, że dla każdej liczby całkowitej nieparzystej  liczba
liczba 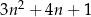 jest podzielna przez 4.
jest podzielna przez 4.
Pokazać, że dla każdej liczby naturalnej  liczba
liczba 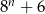 jest podzielna przez 7.
jest podzielna przez 7.
Wykaż, że każda liczba pierwsza większa od 3 jest postaci 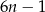 lub
lub 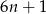 dla pewnej liczby naturalnej
dla pewnej liczby naturalnej  .
.
Udowodnij, że każda liczba całkowita 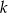 , która przy dzieleniu przez 7 daje resztę 2, ma tę własność, że reszta z dzielenia liczby
, która przy dzieleniu przez 7 daje resztę 2, ma tę własność, że reszta z dzielenia liczby 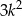 przez 7 jest równa 5.
przez 7 jest równa 5.
Reszta z dzielenia liczby całkowitej  przez 4 jest równa 3. Wyznacz resztę z dzielenia liczby
przez 4 jest równa 3. Wyznacz resztę z dzielenia liczby 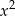 przez 4.
przez 4.
Reszta z dzielenia liczby całkowitej  przez 5 jest równa 4. Wyznacz resztę z dzielenia liczby
przez 5 jest równa 4. Wyznacz resztę z dzielenia liczby 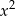 przez 5.
przez 5.
Wykaż, że jeśli  należy do zbioru liczb całkowitych, to
należy do zbioru liczb całkowitych, to 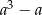 jest podzielne przez 3.
jest podzielne przez 3.
Wykaż, że liczba 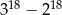 jest podzielna przez 19.
jest podzielna przez 19.
Wykaż, że liczba 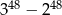 jest podzielna przez 13.
jest podzielna przez 13.
Wyznacz wszystkie pary liczb całkowitych 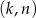 spełniających równość
spełniających równość 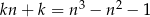 .
.
Wyznacz wszystkie pary 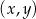 , gdzie
, gdzie  i
i 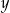 są liczbami całkowitymi spełniającymi równanie
są liczbami całkowitymi spełniającymi równanie
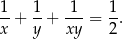
Wyznacz wszystkie liczby całkowite  , dla których liczba
, dla których liczba 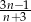 jest liczbą całkowitą.
jest liczbą całkowitą.

