Rzucamy trzy razy monetą, a następnie rzucamy tyle razy kostką, ile orłów otrzymaliśmy w rzutach monetami. Oblicz prawdopodobieństwo tego, że suma oczek otrzymanych w rzutach kostką jest dwa razy większa od liczby orłów otrzymanych w rzutach monetą jeżeli wiadomo, że w rzutach monetą otrzymaliśmy przynajmniej jednego orła.
/Szkoła średnia/Prawdopodobieństwo/Warunkowe i całkowite
W pojemniku jest siedem kul: pięć kul białych i dwie kule czarne. Z tego pojemnika losujemy jednocześnie dwie kule bez zwracania. Następnie – z kul pozostałych w pojemniku – losujemy jeszcze jedną kulę. Oblicz prawdopodobieństwo wylosowania kuli czarnej w drugim losowaniu.
Liczby ze zbioru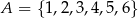 
ustawiamy w losowy sposób w sześcioelementowy ciąg, przy czym każda liczba ze zbioru 
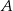jest dokładnie jednym wyrazem tego ciągu. Oblicz prawdopodobieństwo tego, że iloczyn każdych dwóch sąsiednich wyrazów tego ciągu jest liczbą parzystą jeżeli wiadomo, że pierwszy wyraz tego ciągu jest liczbą nieparzystą.
Doświadczenie losowe polega na tym, że losujemy jednocześnie trzy liczby ze zbioru
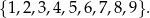
Oblicz prawdopodobieństwo warunkowe, że wśród wylosowanych liczb będzie liczba 3, pod warunkiem, że suma wylosowanych liczb będzie nieparzysta. Wynik przedstaw w postaci ułamka nieskracalnego.
W pudełku znajdują się klocki o różnych kształtach i kolorach. Wiadomo, że prawdopodobieństwo wylosowania klocka, który ma kształt walca lub ma kolor czerwony jest równe 0,6. Prawdopodobieństwo, że losowo wybrany klocek czerwony jest walcem jest równe 0,25. Wiadomo też, że klocki czerwone stanowią 40% wszystkich klocków. Jakie jest prawdopodobieństwo, że losowo wybrany klocek w kształcie walca jest czerwony?
Rzucono kostką do gry trzy razy. Za pierwszym razem nie wyrzucono 4 oczek. Oblicz prawdopodobieństwo, że suma oczek w trzech rzutach jest równa 15.
Z pojemnika zawierającego 10 kul białych i 6 czarnych losujemy jedną kulę i wkładamy zamiast niej jedną kulę czarną. Oblicz prawdopodobieństwo tego, że jeżeli teraz wylosujemy z pojemnika dwie kule, to obie wylosowane kule będą białe.
W każdej z dwóch urn jest tyle samo kul białych i czarnych, a trzecia urna jest pusta. Z każdej z dwóch pierwszych urn losujemy jedną kulę i wkładamy je do trzeciej urny. Następnie z trzeciej urny losujemy jedną kulę. Oblicz prawdopodobieństwo tego, że kula wylosowana z trzeciej urny jest biała.
Ukryj
Podobne zadania
W każdej z dwóch szuflad jest tyle samo rękawiczek prawych i lewych, a trzecia szuflada jest pusta. Z każdej z dwóch pierwszych szuflad losujemy jedną rękawiczkę i wkładamy je do trzeciej szuflady. Następnie z trzeciej szuflady losujemy jedną rękawiczkę. Oblicz prawdopodobieństwo tego, że rękawiczka wylosowana z trzeciej szuflady jest lewa.
W pudełku znajdują się 4 kostki do gry: 3 sześcienne (ze ścianami ponumerowanymi liczbami od 1 do 6) i jedna czworościenna (ze ścianami ponumerowanymi liczbami od 1 do 4). Losowo wybrano kostkę, wykonano nią 3 rzuty i w wyniku tych 3 rzutów otrzymano trzy razy jedynkę. Jakie jest prawdopodobieństwo, że wybrana kostka była kostką czworościenną?
Z talii 24 kart wyjęto losowo 1 kartę i odłożono na bok. Następnie wylosowano 2 karty. Oblicz prawdopodobieństwo, że za drugim razem wylosowano 2 kiery.
Rzucamy dziesięciokrotnie monetą. Wśród otrzymanych wyników dokładnie sześć razy otrzymaliśmy orła. Jakie jest prawdopodobieństwo, że w każdym z dwóch pierwszych rzutów otrzymaliśmy reszkę?
Wśród 200 uczniów pewnego krakowskiego gimnazjum przeprowadzono ankietę dotyczącą planów wakacyjnych. Wyniki ankiety przedstawiono w tabeli.
| Klasa | Liczba uczniów | Liczba uczniów, którzy nie wyjadą na wakacje | Liczba uczniów, którzy wyjadą z rodzicami | Liczba uczniów, którzy wyjadą na kolonie |
| Pierwsza | 50 | 8 | 36 | 12 |
| Druga | 80 | 16 | 48 | 24 |
| Trzecia | 70 | 12 | 40 | 24 |
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że losowo wybrana osoba, spośród ankietowanych, wyjedzie na wakacje, jeśli wiadomo, że ta osoba nie jest uczniem drugiej klasy.
Rzucamy dwa razy sześcienną kostką do gry. Oblicz prawdopodobieństwo wyrzucenia dwa razy nieparzystej liczby oczek, jeżeli wiadomo, że pięć oczek nie wypadło ani razu.
Z talii 52 kart wylosowano dwie karty i, nie oglądając ich, włożono do drugiej talii. W ten sposób powstała talia złożona z 54 kart. Oblicz prawdopodobieństwo wylosowania asa z tak utworzonej talii kart.
Doświadczenie losowe polega na tym, że losujemy bez zwracania trzy liczby ze zbioru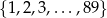 
. Oblicz prawdopodobieństwo, że wśród wylosowanych liczb jest liczba parzysta, jeżeli wiadomo, że pierwsza z wylosowanych liczb jest nieparzysta.
Wśród uczniów pewnej szkoły przeprowadzono ankietę dotyczącą posiadanego rodzeństwa i okazało się, że:
– prawdopodobieństwo, że losowo wybrany uczeń ma brata jest równe 0,6;
– jeżeli wybierzemy losowo ucznia, który ma brata, to prawdopodobieństwo, że ten uczeń ma również siostrę jest równe 0,3;
– jeżeli wybierzemy losowo ucznia, który ma brata i ma siostrę, to prawdopodobieństwo, że ten uczeń jest uczniem klasy pierwszej jest równe 0,4.
Oblicz jakie jest prawdopodobieństwo, że losowo wybrany uczeń tej szkoły jest uczniem klasy pierwszej, który ma brata i siostrę.
W klasach 3a, 3b i 3c przeprowadzono sprawdzian. Losowo wybieramy klasę, a następnie ucznia z tej klasy. Jakie jest prawdopodobieństwo, że wybrany uczeń otrzymał ocenę co najmniej 4, jeżeli wiadomo, że
w klasie 3a: wszystkich uczniów jest 20, uczniów z oceną co najmiej cztery jest 8;
w klasie 3b: wszystkich uczniów jest 21, uczniów z oceną co najmiej cztery jest 14;
w klasie 3c: wszystkich uczniów jest 18, uczniów z oceną co najmiej cztery jest 6.
W dwóch urnach znajdują się kule białe i czarne, przy czym w pierwszej jest 6 kul białych i 4 czarne, a w drugiej urnie 5 białych i 5 czarnych. Rzucamy raz symetryczną kostką do gry. Jeżeli wyrzucimy co najmniej 4 oczka to losujemy 2 kule z pierwszej urny, a jeżeli wyrzucimy co najwyżej 3 oczka to losujemy 2 kule z drugiej urny. Oblicz prawdopodobieństwo wylosowania dwóch kul białych.
Wśród dziesięciu losów loteryjnych znajduje się jeden los z główną wygraną oraz dwa losy uprawniające do wylosowania następnego losu. Oblicz prawdopodobieństwo wygrania przy zakupie jednego losu.
Rzucamy raz sześcienną kostką do gry, a następnie rzucamy tyloma monetami, ile oczek wypadło na kostce. Oblicz prawdopodobieństwo tego, że dokładnie na jednej z wyrzuconych monet jest reszka. Wynik podaj w postaci ułamka nieskracalnego.
