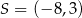Zadanie nr 4103873
Prosta przechodząca przez punkty 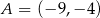 i
i 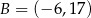 jest styczna do okręgu o środku w punkcie
jest styczna do okręgu o środku w punkcie 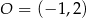 . Oblicz promień tego okręgu i współrzędne punktu styczności tego okręgu z prostą
. Oblicz promień tego okręgu i współrzędne punktu styczności tego okręgu z prostą 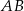 .
.
Rozwiązanie
Naszkicujmy opisaną sytuację.
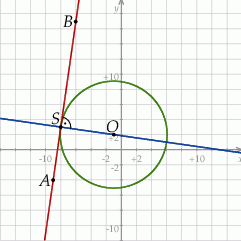
Zaczniemy od wyznaczenia równania prostej 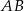 – szukamy prostej w postaci
– szukamy prostej w postaci 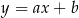 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 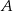 i
i 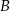 .
.
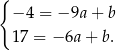
Odejmujemy od drugiego równania pierwsze i mamy
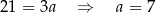
Stąd 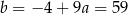 i prosta
i prosta 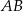 ma równanie
ma równanie 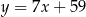 .
.
Sposób I
Promień interesującego nas okręgu moglibyśmy łatwo wyznaczyć ze wzoru na odległość punktu 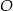 od prostej
od prostej 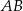 , ale ponieważ i tak mamy wyznaczyć współrzędne punktu styczności
, ale ponieważ i tak mamy wyznaczyć współrzędne punktu styczności 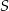 okręgu z prostą
okręgu z prostą 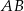 , promień obliczymy jako długość odcinka
, promień obliczymy jako długość odcinka 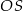 .
.
Prosta  jest prostopadła do prostej
jest prostopadła do prostej 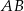 , więc jest to prosta postaci
, więc jest to prosta postaci 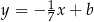 . Współczynnik
. Współczynnik 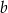 wyznaczmy podstawiając współrzędne punktu
wyznaczmy podstawiając współrzędne punktu 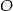
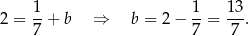
Wyznaczmy teraz punkt wspólny 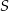 tej prostej z prostą
tej prostej z prostą 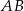 .
.
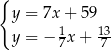
Porównujemy prawe strony tych równości
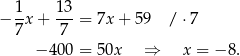
Stąd 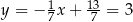 i
i 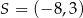 . Pozostało obliczyć promień okręgu
. Pozostało obliczyć promień okręgu
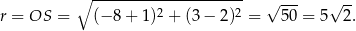
Sposób II
Równanie okręgu o środku w punkcie 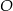 jest postaci
jest postaci
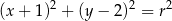
Sprawdźmy kiedy okrąg tej postaci jest styczny do prostej 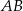 – podstawiamy w tym równaniu
– podstawiamy w tym równaniu 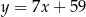 .
.
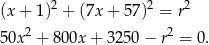
Równanie to powinno mieć dokładnie jedno rozwiązanie (bo prosta 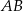 i okrąg mają mieć dokładnie jeden punkt wspólny), więc
i okrąg mają mieć dokładnie jeden punkt wspólny), więc
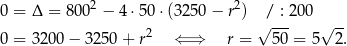
Dla tej wartości  , otrzymane wyżej równanie kwadratowe przyjmuje postać
, otrzymane wyżej równanie kwadratowe przyjmuje postać
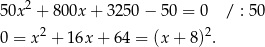
Zatem 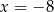 ,
,  i szukany punkt styczności to
i szukany punkt styczności to 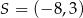 .
.
Odpowiedź: 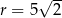 ,
,