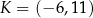Zadanie nr 9553446
Okrąg 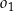 o środku w punkcie
o środku w punkcie 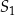 jest określony równaniem
jest określony równaniem 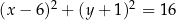 . Okrąg
. Okrąg 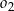 ma środek w punkcie
ma środek w punkcie 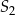 takim, że
takim, że ![−→ S 1S2 = [− 4,4]](https://img.zadania.info/zad/9553446/HzadT5x.png) . Promienie tych okręgów są sobie równe. Figura
. Promienie tych okręgów są sobie równe. Figura 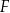 składa się z dwóch okręgów:
składa się z dwóch okręgów: 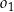 oraz
oraz 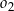 . Punkty
. Punkty 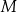 i
i 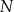 są punktami przecięcia figury
są punktami przecięcia figury 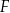 z tą z jej osi symetrii, która jest prostą o dodatnim współczynniku kierunkowym. Wyznacz punkt
z tą z jej osi symetrii, która jest prostą o dodatnim współczynniku kierunkowym. Wyznacz punkt 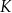 , leżący na jednej z osi symetrii figury
, leżący na jednej z osi symetrii figury 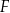 , taki, że pole trójkąta
, taki, że pole trójkąta 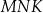 jest równe 40.
jest równe 40.
Rozwiązanie
Okrąg 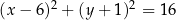 ma środek w punkcie
ma środek w punkcie 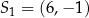 i promień
i promień 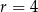 . Wiemy ponadto, że
. Wiemy ponadto, że
![−→ [− 4,4] = S1S2 = S 2 − S 1 S 2 = S1 + [− 4 ,4 ] = (6,− 1)+ [− 4,4] = (2,3).](https://img.zadania.info/zad/9553446/HzadR3x.png)
Możemy teraz naszkicować opisaną sytuację.
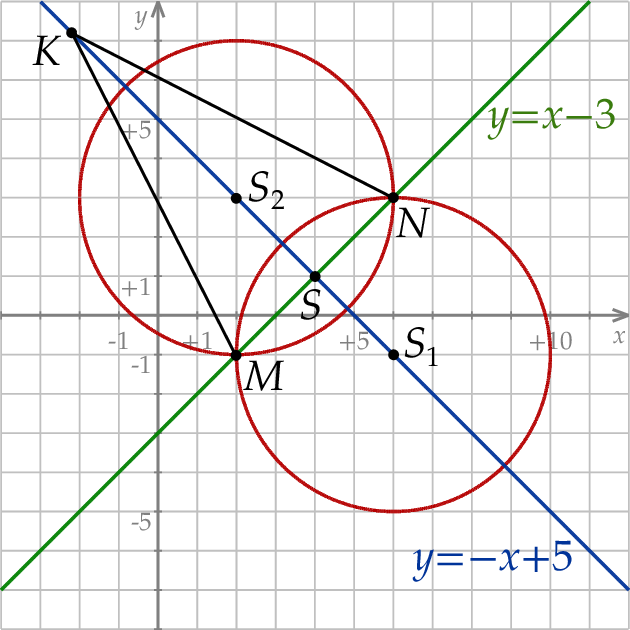
Figura 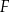 ma oczywiście dwie osie symetrii – jedna z nich to prosta
ma oczywiście dwie osie symetrii – jedna z nich to prosta 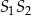 , a druga to prostopadła do niej prosta przechodząca przez punkty wspólne dwóch okręgów. Wyznaczmy równania tych osi symetrii. Równania prostej
, a druga to prostopadła do niej prosta przechodząca przez punkty wspólne dwóch okręgów. Wyznaczmy równania tych osi symetrii. Równania prostej 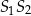 szukamy w postaci
szukamy w postaci 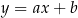 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 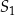 i
i 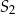 .
.
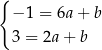
Odejmujemy od pierwszego równania drugie i mamy
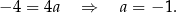
Stąd 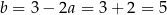 i prosta
i prosta 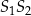 ma równanie
ma równanie 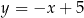 .
.
Druga oś symetrii jest prostopadła do 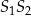 , więc ma równanie postaci
, więc ma równanie postaci 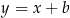 . Jest ona ponadto symetralną odcinka
. Jest ona ponadto symetralną odcinka 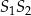 , więc przechodzi przez jego środek
, więc przechodzi przez jego środek
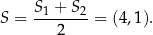
To pozwala wyznaczyć 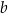 .
.
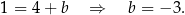
Prosta 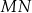 ma więc równanie
ma więc równanie 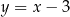 .
.
Wyznaczmy teraz współrzędne punktów 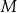 i
i 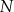 . Podstawiamy
. Podstawiamy 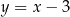 do równania okręgu
do równania okręgu 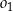 .
.
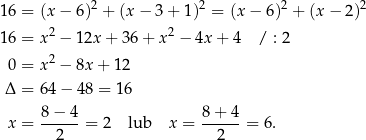
Mamy wtedy 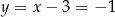 i
i 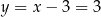 odpowiednio. Zatem
odpowiednio. Zatem 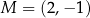 i
i 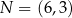 (lub odwrotnie - ale nie ma to znaczenia z punktu widzenia dalszej części rozwiązania).
(lub odwrotnie - ale nie ma to znaczenia z punktu widzenia dalszej części rozwiązania).
Gdyby punkt 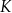 leżał na prostej
leżał na prostej 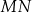 , to pole trójkąta
, to pole trójkąta 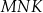 byłoby równe 0, więc punkt
byłoby równe 0, więc punkt 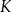 musi leżeć na prostej
musi leżeć na prostej 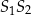 , czyli ma współrzędne postaci
, czyli ma współrzędne postaci 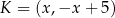 . Mamy ponadto
. Mamy ponadto
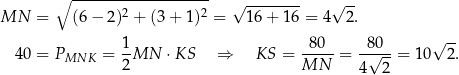
Ta informacja wystarczy do wyznaczenia współrzędnych punktu 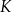 . Zrobimy to na dwa sposoby.
. Zrobimy to na dwa sposoby.
Sposób I
Liczymy
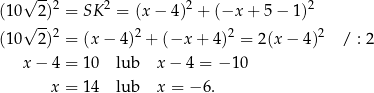
Mamy wtedy 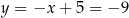 i
i 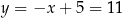 odpowiednio. Zatem
odpowiednio. Zatem 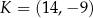 kub
kub 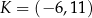 .
.
Sposób II
Korzystamy ze wzoru na odległość d(P,l) punktu 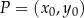 od prostej
od prostej 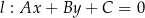 :
:
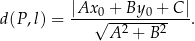
Mamy zatem
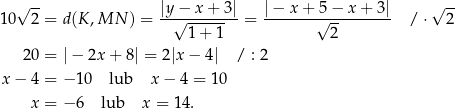
Mamy wtedy 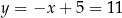 i
i 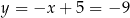 odpowiednio. Zatem
odpowiednio. Zatem 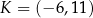 kub
kub 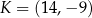 .
.
Odpowiedź: 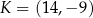 kub
kub