/Gimnazjum/Egzamin gimnazjalny
Próbny Egzamin Gimnazjalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 29 marca 2014 Czas pracy: 90 minut
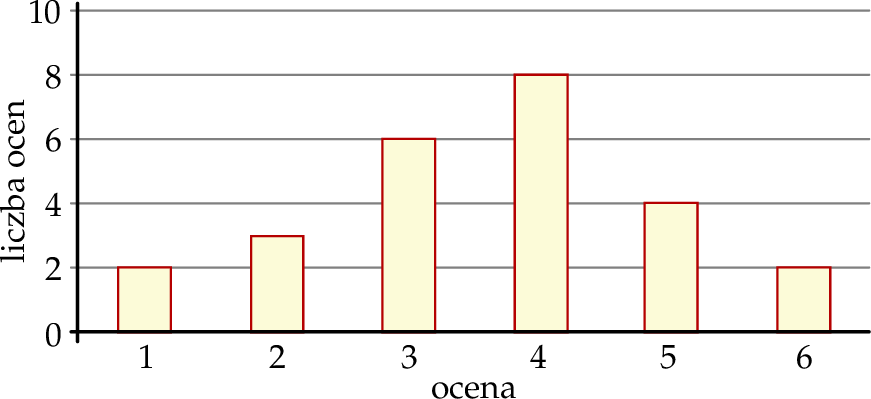
Na diagramie przedstawiono wyniki pracy klasowej z matematyki w pewnej klasie.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Z informacji podanych na diagramie wynika, że
A) pracę klasową pisało 24 uczniów.
B) najczęściej powtarzającą się oceną jest 3.
C) mediana wyników z pracy klasowej wynosi 4.
D) średnia wyników z pracy klasowej jest równa 3,5.
Korzystając z tego, że 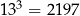 i
i 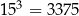 , oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
, oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
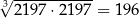 | P | F |
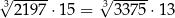 | P | F |
Informacja do zadań 3 i 4
W tabeli przedstawiono informacje dotyczące wyników sprawdzianu z matematyki.
| Ocena | Liczba uczniów |
| 2 | 3 |
| 3 | 8 |
| 4 | 5 |
| 5 | 4 |
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Mediana wystawionych ocen jest równa
A) 2 B) 2,5 C) 3 D) 3,5
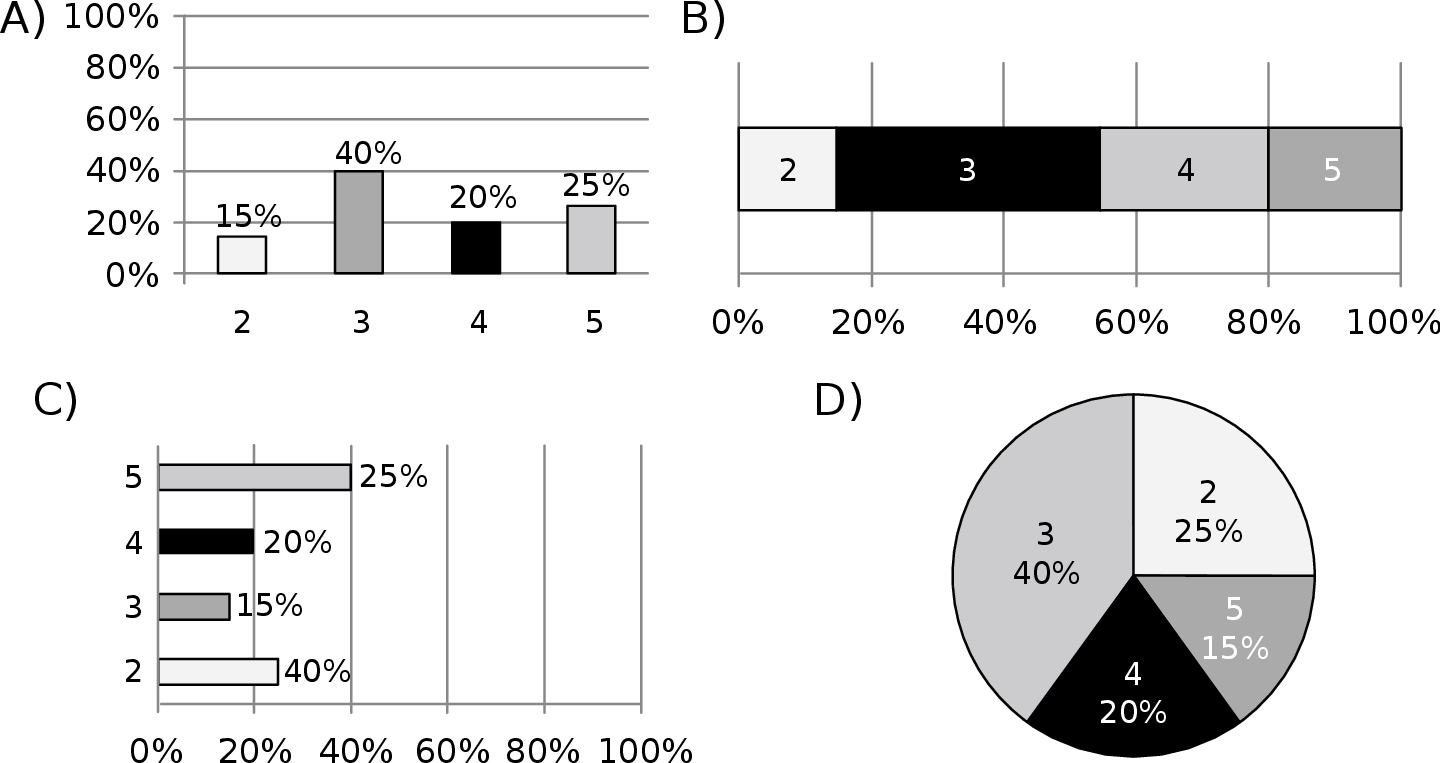
Na którym diagramie poprawnie przedstawiono procentowy podział uczniów ze względu na uzyskaną ocenę? Wybierz odpowiedź spośród podanych.
Na rysunku przedstawiono wykres pewnej funkcji.
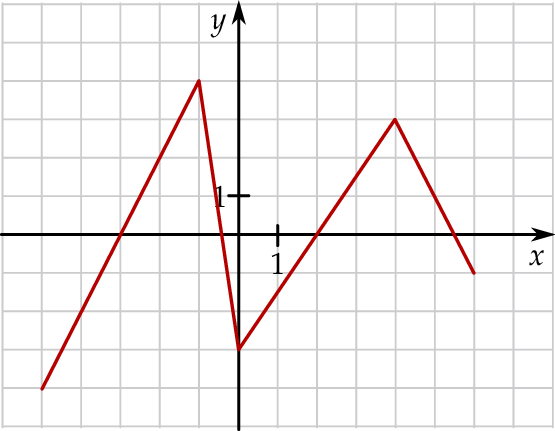
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Funkcja przyjmuje wartość 3 dla 4 argumentów. | P | F |
Dla wszystkich argumentów 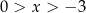 funkcja przyjmuje wartości dodatnie. funkcja przyjmuje wartości dodatnie. | P | F |
Cena brutto = cena netto + podatek VAT
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Jeżeli stawka podatku VAT jest równa 22% i cenna brutto towaru jest równa 4392 zł to cena netto tego towaru jest równa
A) 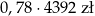 B)
B) 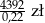 C)
C) 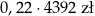 D)
D) 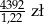
Dane są liczby 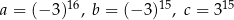 .
.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Liczby te uporządkowane od największej do najmniejszej to:
A) 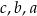 B)
B) 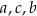 C)
C) 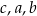 D)
D) 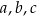
Pan Kazimierz chce kupić 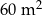 papy. Papa jest sprzedawana w rolkach o szerokości 1 m. Pan Kazimierz pod uwagę wziął dwa rodzaje papy.
papy. Papa jest sprzedawana w rolkach o szerokości 1 m. Pan Kazimierz pod uwagę wziął dwa rodzaje papy.
| Typ papy | Długość papy w rolce | Cena papy |
| I rodzaj | 15 m | 75 zł za 1 rolkę |
| II rodzaj | 3 m | 6 zł za 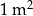 |
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Cena  papy I rodzaju jest niższa niż cena papy I rodzaju jest niższa niż cena 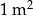 papy II rodzaju. papy II rodzaju. | P | F |
| Kupując tańszą papę, pan Kazimierz zaoszczędzi 40 zł. | P | F |
W pudełku jest 30 kul białych i 20 czarnych. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jeżeli 10 kul białych zostanie zastąpionych kulami czarnymi, to prawdopodobieństwa wylosowania kuli czarnej i białej będą równe. | P | F |
| Jeżeli podwoimy liczbę kul czarnych w pudełku, to prawdopodobieństwo wylosowania kuli czarnej wzrośnie dwukrotnie. | P | F |
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Odległość na osi liczbowej między największą i najmniejszą spośród liczb: 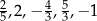 jest równa
jest równa
A)  B)
B) 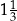 C)
C) 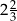 D)
D) 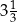
Informacja do zadań 11 i 12
Ola przygotowując się do egzaminu rozwiązywała zadania z matematyki. Wykres przedstawia liczbę rozwiązanych zadań w zależności od czasu.
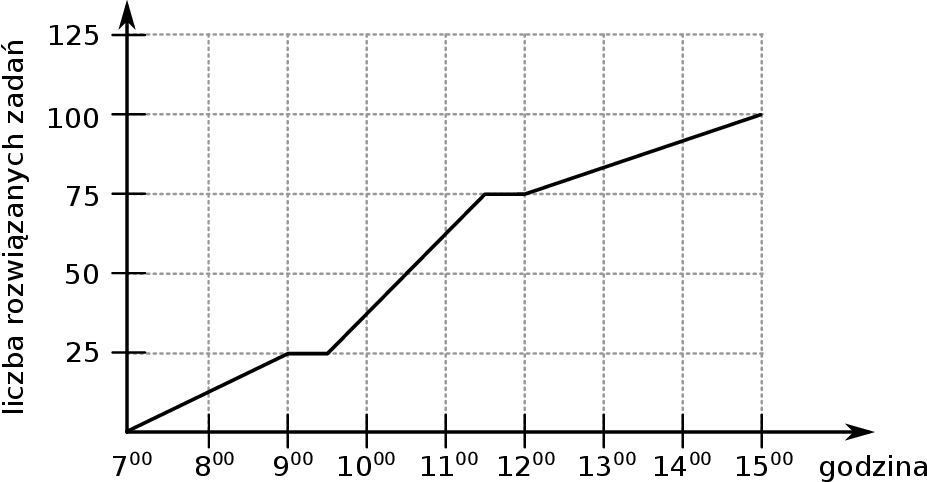
Na podstawie wykresu wybierz zdanie fałszywe.
A) O godzinie 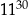 Ola rozpoczęła przerwę.
Ola rozpoczęła przerwę.
B) Od 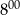 do
do 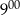 Ola rozwiązała mniej zadań niż od
Ola rozwiązała mniej zadań niż od 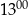 do
do 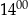 .
.
C) Od 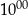 do
do 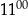 Ola rozwiązywała zadania w tempie 25 zadań na godzinę.
Ola rozwiązywała zadania w tempie 25 zadań na godzinę.
D) Przez ostatnie trzy godziny Ola rozwiązała 25 zadań.
Kolejnego dnia Ola ponownie rozwiązywała zadania, ale poświęciła na to 6 godzin. Okazało się jednak, że średnie tempo rozwiązywania zadań było identyczne, jak w dniu przedstawionym na wykresie. Ile zadań Ola rozwiązała drugiego dania nauki? Wybierz odpowiedź spośród podanych.
A) 75 B) 80 C) 90 D) 60
Ula w trakcie loterii charytatywnej sprzedawała dwa rodzaje losów: losy za 5 złotych i losy za 7 złotych. W sumie sprzedała 92 losy, przy czym sprzedała 3 razy więcej losów za 5 zł, niż losów za 7 złotych. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Liczba sprzedanych losów za 5 złotych była o 46 większa od liczby sprzedanych losów za 7 złotych. | P | F |
| Wartość sprzedanych losów wyniosła: 500 zł. | P | F |
W równoległoboku 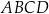 bok
bok 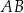 jest dwa razy dłuższy od boku
jest dwa razy dłuższy od boku 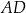 . Punkt
. Punkt 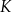 jest środkiem boku
jest środkiem boku 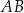 , a punkt
, a punkt 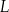 jest środkiem boku
jest środkiem boku 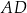 .
.
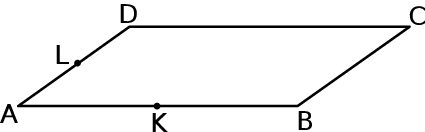
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 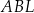 ma takie samo pole, jak trójkąt ma takie samo pole, jak trójkąt 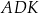 . . | P | F |
Pole równoległoboku 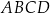 jest cztery razy większe od pola trójkąta jest cztery razy większe od pola trójkąta 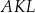 . . | P | F |
Piechur porusza się z prędkością 5 km/h. Każdy jego krok ma długość 62,5 cm.
Ile kroków wykona piechur w czasie 15 minut? Wybierz odpowiedź spośród podanych.
A) 1000 kroków B) 2000 kroków C) 200 kroków D) 100 kroków
Dwa sąsiednie kąty wewnętrzne czworokąta mają miarę  , trzeci ma miarę o
, trzeci ma miarę o 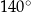 większą niż kąt
większą niż kąt  , a czwarty ma miarę osiem razy większą niż kąt
, a czwarty ma miarę osiem razy większą niż kąt  .
.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Czworokąt ten jest
A) prostokątem. B) równoległobokiem. C) deltoidem. D) trapezem.
Z kwadratowego kartonika o boku długości 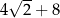 odcięto naroża, tak jak pokazano na rysunku i otrzymano ośmiokąt foremny.
odcięto naroża, tak jak pokazano na rysunku i otrzymano ośmiokąt foremny.
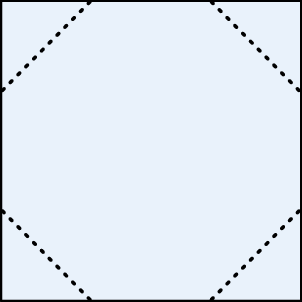
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Bok ośmiokąta ma długość 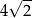 . . | P | F |
| Suma pól odciętych naroży jest równa 24. | P | F |
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Pole równoległoboku przedstawionego na rysunku jest równe
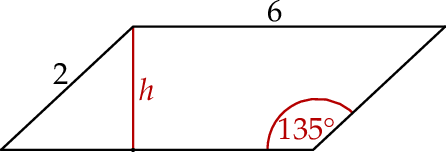
A) 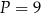 B)
B) 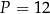 C)
C) 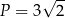 D)
D) 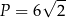
Dwie proste równoległe 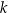 i
i 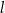 przecięto prostymi
przecięto prostymi 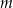 i
i  w sposób przedstawiony na rysunku.
w sposób przedstawiony na rysunku.
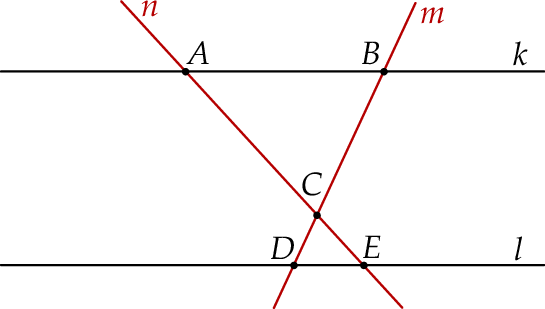
Czy trójkąty 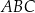 i
i 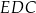 są podobne? Wybierz odpowiedź T albo N oraz jej uzasadnienie spośród zdań oznaczonych literami A–D.
są podobne? Wybierz odpowiedź T albo N oraz jej uzasadnienie spośród zdań oznaczonych literami A–D.
| Tak | Nie |
| ponieważ | |
| A) | te trójkąty mają wspólny wierzchołek. |
| B) | te trójkąty mają boki różnej długości. |
| C) | te trójkąty mają odpowiednie kąty równej miary. |
| D) | te trójkąty są przystające. |
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Suma objętości 2 kul, z których każda ma promień 1, jest taka sama jak objętość jednej kuli o promieniu
A) 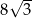 B)
B) 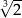 C)
C) 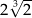 D) 2
D) 2
Jacek, Marek, Karol i Andrzej kupili losy na loterii, przy czym Jacek kupił losy za 24 zł, Marek kupił losy za 36 zł, a Karol i Andrzej kupili losy za 30 złoty każdy. Wśród kupionych losów jeden okazał się być wygrywającym i chłopcy otrzymali 600 zł nagrody. Otrzymaną kwotę chłopcy podzielili następująco: każdy otrzymał zwrot kosztów zakupu losów, a pozostałą kwotę podzieli pomiędzy siebie proporcjonalnie do kwot, które przeznaczyli na zakup losów. Ile pieniędzy z nagrody (nie licząc zwrotu kosztów zakupu losów) otrzymał Marek? Zapisz obliczenia.
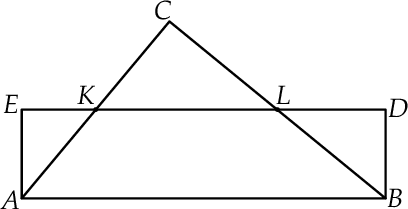
Na rysunku przedstawiono prostokąt 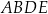 i trójkąt
i trójkąt 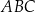 . Punkty
. Punkty 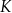 i
i 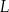 dzielą odcinki
dzielą odcinki 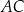 i
i 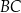 na połowy. Uzasadnij, że pole prostokąta
na połowy. Uzasadnij, że pole prostokąta 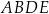 jest równe polu trójkąta
jest równe polu trójkąta 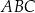 .
.
Pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego jest równe 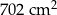 . Pole podstawy tej bryły stanowi 60% pola powierzchni jednej ściany bocznej. Oblicz wysokość bryły. Zapisz obliczenia.
. Pole podstawy tej bryły stanowi 60% pola powierzchni jednej ściany bocznej. Oblicz wysokość bryły. Zapisz obliczenia.

