Zadanie nr 4913698
Wyznacz wszystkie wartości parametru 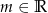 , dla których równanie
, dla których równanie
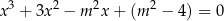
ma trzy różne pierwiastki, z których jeden jest ujemny, a pozostałe dwa należą do przedziału ![[ ] 1 2 ,5](https://img.zadania.info/zad/4913698/HzadT2x.png) .
.
Rozwiązanie
Najtrudniejsze w tym zadaniu, to znaleźć punkt zaczepienia – żeby w ogóle zacząć coś liczyć. Jeżeli chwilę pobawimy się danym równaniem, to można zauważyć, że suma współczynników przy  –ach jest równa 0. To oznacza, że
–ach jest równa 0. To oznacza, że 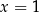 jest jednym z pierwiastków tego równania. Dzielimy więc lewą stronę przez
jest jednym z pierwiastków tego równania. Dzielimy więc lewą stronę przez 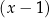 . My jak zawsze zrobimy to grupując wyrazy.
. My jak zawsze zrobimy to grupując wyrazy.
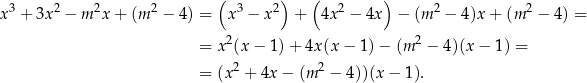
Teraz sprawa jest już dużo prostsza, bo pozostała nam analiza trójmianu w pierwszym nawiasie. Wyjściowe równanie ma mieć trzy różne pierwiastki, więc trójmian musi mieć dwa różne pierwiastki i żaden z nich nie może być równy 1. Sprawdźmy najpierw, kiedy 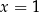 jest pierwiastkiem tego trójmianu.
jest pierwiastkiem tego trójmianu.
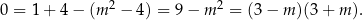
Musi więc być 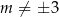 . Liczymy teraz
. Liczymy teraz 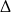 –ę.
–ę.
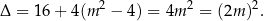
Równanie kwadratowe ma więc dwa różne pierwiastki jeżeli 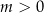 . Przy tym założeniu łatwo obliczyć te pierwiastki
. Przy tym założeniu łatwo obliczyć te pierwiastki
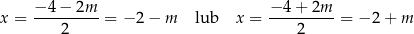
(zauważmy, że gdybyśmy za pierwiastek z 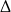 –y wzięli
–y wzięli 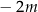 , to otrzymalibyśmy dokładnie te same pierwiastki).
, to otrzymalibyśmy dokładnie te same pierwiastki).
Teraz w sumie jest prosta sprawa – mniejszy z tych pierwiastków ma być ujemny, a większy ma być w przedziale ![[ ] 12,5](https://img.zadania.info/zad/4913698/HzadR13x.png) . Niestety nie wiemy jaki jest znak
. Niestety nie wiemy jaki jest znak 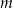 , więc nie wiemy który z tych pierwiastków jest większy, a który jest mniejszy. Rozważmy więc dwa przypadki.
, więc nie wiemy który z tych pierwiastków jest większy, a który jest mniejszy. Rozważmy więc dwa przypadki.
Jeżeli 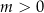 , muszą być spełnione nierówności
, muszą być spełnione nierówności
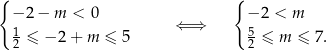
W tym przypadku mamy więc ![[5 ) m ∈ 2,3 ∪ (3,7]](https://img.zadania.info/zad/4913698/HzadR17x.png) (bo
(bo 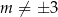 ). Jeżeli natomiast
). Jeżeli natomiast 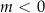 , to muszą być spełnione nierówności
, to muszą być spełnione nierówności
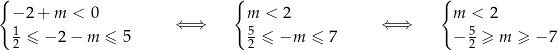
W tym przypadku mamy więc ![m ∈ [− 7,− 3)∪ (− 3,− 5 ] 2](https://img.zadania.info/zad/4913698/HzadR21x.png) . Łączymy oba przypadki i otrzymujemy rozwiązanie
. Łączymy oba przypadki i otrzymujemy rozwiązanie
![( 5] [ 5 ) m ∈ [−7 ,−3 )∪ − 3,− -- ∪ -,3 ∪ (3,7 ]. 2 2](https://img.zadania.info/zad/4913698/HzadR22x.png)
Odpowiedź: ![( ] [ ) m ∈ [−7 ,−3 )∪ − 3,− 52 ∪ 52,3 ∪ (3,7]](https://img.zadania.info/zad/4913698/HzadR23x.png)

