Obwód trójkąta prostokątnego wynosi 60 cm, a tangens jednego z kątów ostrych jest równy 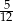 . Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego na przeciwprostokątną.
. Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego na przeciwprostokątną.
/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny
Obwód trójkąta prostokątnego wynosi 72 cm, a tangens jednego z kątów ostrych jest równy 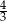 . Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego na przeciwprostokątną.
. Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego na przeciwprostokątną.
Dany jest trójkąt prostokątny o polu 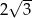 i kącie ostrym
i kącie ostrym 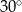 . Oblicz długości przyprostokątnych tego trójkąta.
. Oblicz długości przyprostokątnych tego trójkąta.
Dany jest trójkąt prostokątny o polu 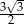 i kącie ostrym
i kącie ostrym 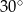 . Oblicz długości przyprostokątnych tego trójkąta.
. Oblicz długości przyprostokątnych tego trójkąta.
Dany jest trójkąt prostokątny o polu 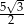 i kącie ostrym
i kącie ostrym  . Oblicz długości przyprostokątnych tego trójkąta.
. Oblicz długości przyprostokątnych tego trójkąta.
Dany jest trójkąt prostokątny 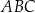 , w którym
, w którym 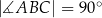 oraz
oraz 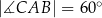 . Punkty
. Punkty  i
i  leżą na bokach – odpowiednio –
leżą na bokach – odpowiednio – 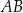 i
i 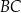 tak, że
tak, że 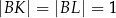 (zobacz rysunek). Odcinek
(zobacz rysunek). Odcinek 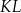 przecina wysokość
przecina wysokość 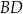 tego trójkąta w punkcie
tego trójkąta w punkcie 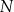 , a ponadto
, a ponadto 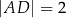 .
.
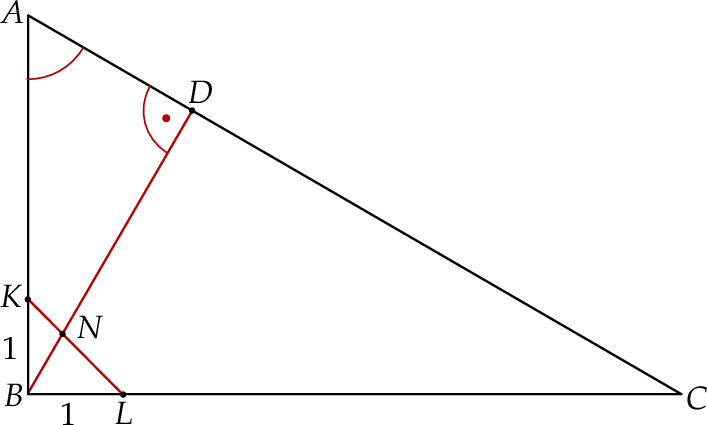
Wykaż, że 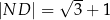 .
.
Wykaż, że wysokość 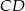 trójkąta prostokątnego
trójkąta prostokątnego 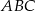 poprowadzona z wierzchołka
poprowadzona z wierzchołka 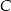 kąta prostego dzieli przeciwprostokątną na odcinki
kąta prostego dzieli przeciwprostokątną na odcinki 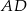 i
i 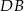 , których stosunek długości jest równy stosunkowi kwadratów długości przyprostokątnych odpowiednio
, których stosunek długości jest równy stosunkowi kwadratów długości przyprostokątnych odpowiednio 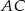 i
i 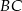 tego trójkąta.
tego trójkąta.
Na okręgu o promieniu 1 opisano trójkąt prostokątny, którego przyprostokątne mają długości  i
i 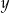 .
.
- Wyznacz
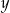 jako funkcję
jako funkcję  i określ dziedzinę tej funkcji.
i określ dziedzinę tej funkcji. - Sporządź wykres tej funkcji.
Na zewnątrz trójkąta prostokątnego 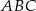 , w którym
, w którym 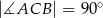 oraz
oraz 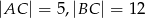 zbudowano kwadrat
zbudowano kwadrat  .
.
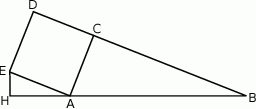
Punkt  leży na prostej
leży na prostej 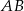 i kąt
i kąt 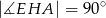 . Oblicz pole trójkąta
. Oblicz pole trójkąta 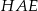 .
.
Dany jest trójkąt prostokątny 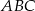 , w którym
, w którym 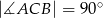 i
i 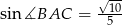 . Niech
. Niech 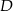 oznacza punkt wspólny wysokości poprowadzonej z wierzchołka
oznacza punkt wspólny wysokości poprowadzonej z wierzchołka 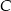 kąta prostego i przeciwprostokątnej
kąta prostego i przeciwprostokątnej 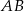 tego trójkąta. Wykaż, że
tego trójkąta. Wykaż, że 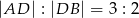 .
.
W trójkąt prostokątny 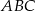 o przyprostokątnych długości
o przyprostokątnych długości 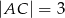 i
i 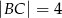 wpisano dwa przystające okręgi w ten sposób, że są one wzajemnie styczne oraz jeden z nich jest styczny do boków
wpisano dwa przystające okręgi w ten sposób, że są one wzajemnie styczne oraz jeden z nich jest styczny do boków 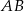 i
i 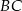 , a drugi do boków
, a drugi do boków 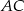 i
i 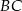 .
.
Oblicz długość promienia tych okręgów.
Dany jest trójkąt prostokątny  , w którym przyprostokątna
, w którym przyprostokątna 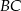 ma długość 6. Punkt
ma długość 6. Punkt 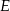 jest środkiem przeciwprostokątnej
jest środkiem przeciwprostokątnej 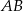 , spodek
, spodek 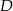 wysokości
wysokości 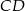 leży między punktami
leży między punktami 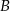 i
i 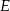 , a odległość między punktami
, a odległość między punktami 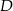 i
i 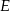 jest równa 7 (zobacz rysunek).
jest równa 7 (zobacz rysunek).
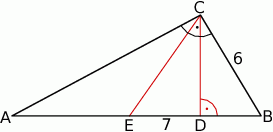
Oblicz obwód trójkąta  .
.
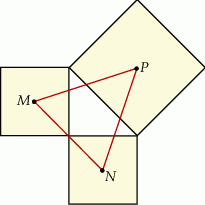
Dany jest trójkąt prostokątny  . Na przyprostokątnych
. Na przyprostokątnych  i
i 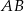 tego trójkąta obrano odpowiednio punkty
tego trójkąta obrano odpowiednio punkty 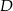 i
i 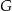 . Na przeciwprostokątnej
. Na przeciwprostokątnej 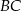 wyznaczono punkty
wyznaczono punkty 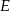 i
i 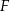 takie, że
takie, że 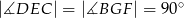 (zobacz rysunek). Wykaż, że trójkąt
(zobacz rysunek). Wykaż, że trójkąt 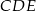 jest podobny do trójkąta
jest podobny do trójkąta 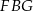 .
.
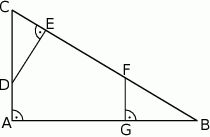
Dany jest trójkąt prostokątny 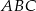 . Na przyprostokątnych
. Na przyprostokątnych 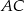 i
i 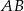 tego trójkąta obrano odpowiednio punkty
tego trójkąta obrano odpowiednio punkty 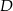 i
i 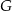 . Na przeciwprostokątnej
. Na przeciwprostokątnej 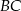 wyznaczono punkty
wyznaczono punkty 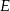 i
i 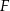 takie, że
takie, że 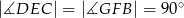 (zobacz rysunek). Wykaż, że trójkąt
(zobacz rysunek). Wykaż, że trójkąt 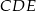 jest podobny do trójkąta
jest podobny do trójkąta  .
.
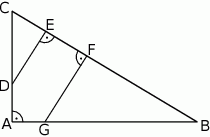
Dany jest trójkąt prostokątny  . Na przyprostokątnych
. Na przyprostokątnych  i
i 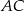 tego trójkąta obrano odpowiednio punkty
tego trójkąta obrano odpowiednio punkty 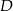 i
i 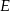 takie, że
takie, że 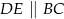 . Na przeciwprostokątnej
. Na przeciwprostokątnej 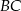 wyznaczono punkt
wyznaczono punkt 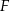 taki, że
taki, że 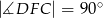 (zobacz rysunek). Wykaż, że trójkąt
(zobacz rysunek). Wykaż, że trójkąt 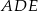 jest podobny do trójkąta
jest podobny do trójkąta 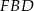 .
.
Na zewnątrz równoramiennego trójkąta prostokątnego o przyprostokątnych równych  zbudowano kwadraty tak, że bok każdego kwadratu jest jednocześnie bokiem trójkąta. Środki symetrii tych kwadratów połączono odcinkami i otrzymano trójkąt
zbudowano kwadraty tak, że bok każdego kwadratu jest jednocześnie bokiem trójkąta. Środki symetrii tych kwadratów połączono odcinkami i otrzymano trójkąt  . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta  jest równe
jest równe 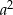 .
.
Na zewnątrz równoramiennego trójkąta prostokątnego 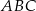 zbudowano kwadraty tak, że bok każdego kwadratu jest jednocześnie bokiem trójkąta. Środki symetrii tych kwadratów połączono odcinkami i otrzymano trójkąt
zbudowano kwadraty tak, że bok każdego kwadratu jest jednocześnie bokiem trójkąta. Środki symetrii tych kwadratów połączono odcinkami i otrzymano trójkąt 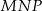 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta  jest dwa razy większe od pola trójkąta
jest dwa razy większe od pola trójkąta  .
.
W trójkącie prostokątnym równoramiennym 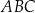 o przeciwprostokątnej
o przeciwprostokątnej 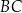 punkt
punkt  jest środkiem ramienia
jest środkiem ramienia 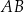 . Odcinek
. Odcinek  ma długość 5 (zobacz rysunek).
ma długość 5 (zobacz rysunek).
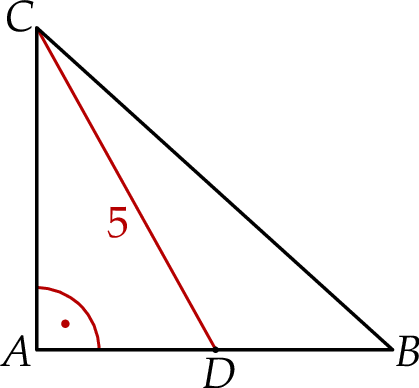
Oblicz obwód trójkąta 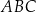 .
.
Uzasadnij, że nie istnieje trójkąt prostokątny, w którym przeciwprostokątna ma długość 24, a kąty ostre  i
i 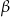 są takie, że
są takie, że 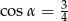 i
i 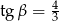 .
.
Oblicz długości boków trójkąta prostokątnego, którego obwód wynosi 70, a pole 210.
Oblicz długości boków trójkąta prostokątnego, którego obwód wynosi 40, a pole 60.
Wykaż, że jeżeli pole koła opisanego na trójkącie prostokątnym jest 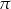 razy większe od pola trójkąta, to trójkąt ten jest równoramienny.
razy większe od pola trójkąta, to trójkąt ten jest równoramienny.
Wysokość trójkąta prostokątnego poprowadzona na przeciwprostokątną dzieli ją na odcinki długości 1 cm i 49 cm. Oblicz pole tego trójkąta.
Przez wierzchołek kąta prostego trójkąta prostokątnego o przyprostokątnych 5 i 12 poprowadzono prostą, która dzieli ten trójkąt na dwa trójkąty o równych obwodach. Znajdź stosunek promieni okręgów wpisanych w otrzymane z podziału trójkąty.
Przez wierzchołek kąta prostego trójkąta prostokątnego o przyprostokątnych 8 i 15 poprowadzono prostą, która dzieli ten trójkąt na dwa trójkąty o równych obwodach. Znajdź stosunek promieni okręgów wpisanych w otrzymane z podziału trójkąty.
Długość przeciwprostokątnej trójkąta prostokątnego o obwodzie 90 jest liczbą całkowitą i jest o 1 większa od długości jednej z przyprostokątnych. Oblicz pole tego trójkąta.
Trójkąty prostokątne równoramienne 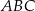 i
i 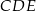 są położone tak, jak na poniższym rysunku (w obu trójkątach kąt przy wierzchołku
są położone tak, jak na poniższym rysunku (w obu trójkątach kąt przy wierzchołku 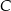 jest prosty). Wykaż, że
jest prosty). Wykaż, że 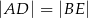 .
.
Trójkąty prostokątne równoramienne 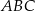 i
i 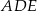 są położone tak, jak na poniższym rysunku.
są położone tak, jak na poniższym rysunku.
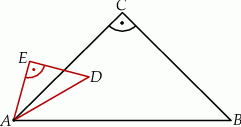
Wykaż, że 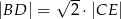 .
.
Jeden z kątów trójkąta prostokątnego ma miarę 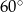 , promień okręgu wpisanego w ten trójkąt ma długość 1. Oblicz długości boków trójkąta.
, promień okręgu wpisanego w ten trójkąt ma długość 1. Oblicz długości boków trójkąta.

