Rzucamy trzy razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia 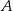 polegającego na tym, że suma liczb wyrzuconych oczek nie jest równa 4.
polegającego na tym, że suma liczb wyrzuconych oczek nie jest równa 4.
/Szkoła średnia/Prawdopodobieństwo/Z definicji/Kostki
Rzucamy trzy razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo otrzymania iloczynu oczek równego 12.
Dane są trzy sześcienne kostki do gry: czerwona, niebieska i zielona. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że przy jednokrotnym rzucie trzema kostkami liczba otrzymana na niebieskiej kostce jest większa niż suma liczb otrzymanych na dwóch pozostałych kostkach.
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo tego, że w każdym rzucie otrzymamy inną liczbę oczek.
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo tego, że iloczyn otrzymanych jest mniejszy od 25.
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo tego, że ani razu nie otrzymamy szóstki.
Oblicz prawdopodobieństwo, że w rzucie dwoma kostkami otrzymamy iloczyn oczek mniejszy od 11.
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo tego, że suma otrzymanych oczek jest równa co najmniej 4.
Rzucamy dwa razy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego oczka do sześciu oczek. Oblicz prawdopodobieństwo zdarzenia 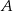 polegającego na tym, że co najwyżej jeden raz wypadnie ścianka z pięcioma oczkami.
polegającego na tym, że co najwyżej jeden raz wypadnie ścianka z pięcioma oczkami.
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo tego, że suma otrzymanych oczek jest równa co najmniej 5.
Rzucamy dwa razy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego oczka do sześciu oczek. Oblicz prawdopodobieństwo zdarzenia 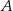 polegającego na tym, że co najmniej jeden raz wypadnie ścianka z pięcioma oczkami.
polegającego na tym, że co najmniej jeden raz wypadnie ścianka z pięcioma oczkami.
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo tego, że liczba oczek w każdym rzucie będzie parzysta lub większa od 3.
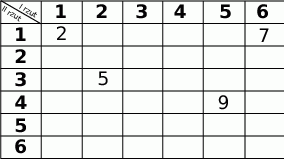
Rzucamy dwa razy symetryczną, sześcienną kostką do gry i zapisujemy sumę liczb wyrzuconych oczek.
- Uzupełnij tabelę, tak aby przedstawiała wszystkie możliwe wyniki tego doświadczenia.
- Oblicz prawdopodobieństwo zdarzenia
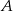 , polegającego na tym, że suma liczb oczek jest liczbą nieparzystą.
, polegającego na tym, że suma liczb oczek jest liczbą nieparzystą. - Oblicz prawdopodobieństwo zdarzenia
 , polegającego na tym, że reszta z dzielenia sumy liczby oczek przez 3 jest równa 2.
, polegającego na tym, że reszta z dzielenia sumy liczby oczek przez 3 jest równa 2.
Rzucamy cztery razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma kwadratów liczb oczek otrzymanych we wszystkich czterech rzutach będzie mniejsza niż 20.
Rzucamy dziesięć razy sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w tych dziesięciu rzutach otrzymaliśmy dokładnie cztery razy sześć oczek, przy czym wyrzucono je w następującej konfiguracji
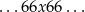
tzn. w pewnym momencie w dwóch kolejnych rzutach otrzymaliśmy szóstki, potem wyrzuciliśmy inną liczbę  oczek, a następnie znowu wyrzuciliśmy dwie szóstki w dwóch kolejnych rzutach.
oczek, a następnie znowu wyrzuciliśmy dwie szóstki w dwóch kolejnych rzutach.
Oblicz prawdopodobieństwo, że w dziesięciu rzutach kostką dokładnie na dwóch kostkach otrzymamy ściankę z dwoma oczkami i dokładnie na trzech kostkach ściankę z trzema oczkami.
Oblicz prawdopodobieństwo, że w trzech rzutach symetryczną sześcienną kostką do gry suma kwadratów liczb wyrzuconych oczek będzie podzielna przez 4.
Rzucamy dwiema sześciennymi kostkami.
- Jakie jest prawdopodobieństwo, że różnica między liczbami oczek wyrzuconych na kostkach (od większej odejmujemy mniejszą) będzie równa 2?
- Jaka jest najbardziej prawdopodobna różnica między wynikami na kostkach (od większego odejmujemy mniejszy)?
Rzucamy trzema kostkami. Prawdopodobieństwo otrzymania sumy oczek równej 3 wynosi 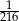 , a prawdopodobieństwo otrzymania sumy oczek równej 4 wynosi
, a prawdopodobieństwo otrzymania sumy oczek równej 4 wynosi 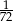 . jakie jest prawdopodobieństwo tego, że suma otrzymanych oczek będzie mniejsza od 5?
. jakie jest prawdopodobieństwo tego, że suma otrzymanych oczek będzie mniejsza od 5?
Rzucamy cztery razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że iloczyn liczb oczek otrzymanych we wszystkich czterech rzutach będzie równy 60 .
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo każdego z następujących zdarzeń:
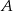 — w każdym rzucie wypadnie nieparzysta liczba oczek.
— w każdym rzucie wypadnie nieparzysta liczba oczek. 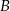 -– suma oczek otrzymanych w obu rzutach jest liczbą większą od 9.
-– suma oczek otrzymanych w obu rzutach jest liczbą większą od 9. 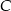 -– suma oczek otrzymanych w obu rzutach jest liczbą nieparzystą i większą od 9.
-– suma oczek otrzymanych w obu rzutach jest liczbą nieparzystą i większą od 9.
Oblicz prawdopodobieństwo, że w rzucie pięcioma sześciennymi kostkami do gry otrzymamy sumę oczek różną od 28.
Na jednej kostce sześciennej znajdują się liczby: 2,3,3,6,6,6, a na drugiej: 1,1,4,6,7,7. Gra polega na rzucie wybraną kostką. Wygrywa ten, kto wyrzuci większą liczbę na swojej kostce. Masz prawo wyboru kostki. Którą kostkę należy wybrać, aby mieć większe szanse wygranej?
Rzucono dwiema sześciennymi kostkami do gry i określono zdarzenia: 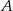 – na każdej kostce wypadła inna liczba oczek,
– na każdej kostce wypadła inna liczba oczek, 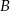 – suma oczek jest mniejsza od 6. Oblicz prawdopodobieństwo zdarzenia
– suma oczek jest mniejsza od 6. Oblicz prawdopodobieństwo zdarzenia 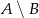 .
.
Rzucamy dwukrotnie kostką, które ze zdarzeń jest bardziej prawdopodobne: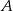 – w pierwszym rzucie otrzymamy liczbę oczek mniejszą niż w drugim;
– w pierwszym rzucie otrzymamy liczbę oczek mniejszą niż w drugim;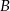 – suma oczek, jakie wypadną w obydwu rzutach, jest nie mniejsza od 8?
– suma oczek, jakie wypadną w obydwu rzutach, jest nie mniejsza od 8?
Rzucamy 9 razy symetryczną 6-ścienną kostką do gry. Jakie jest prawdopodobieństwo, że w każdych trzech kolejnych rzutach otrzymamy trzy różne liczby oczek?
Rzucamy trzy razy kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w trzecim rzucie otrzymamy dwa razy więcej oczek niż w pierwszym rzucie.
Rzucamy trzy razy kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w pierwszym rzucie otrzymamy dwa razy więcej oczek niż w trzecim rzucie.
Rzucamy dwiema sześciennymi kostkami. Jakie jest prawdopodobieństwo, że na pierwszej kostce wypadło dwa razy mniej oczek niż na drugiej?
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo otrzymania iloczynu oczek równego 6.
Rzucamy dwa razy kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w drugim rzucie wypadnie parzysta liczba oczek.
Gracz rzuca dwukrotnie symetryczną sześcienną kostką do gry i oblicza wartość bezwzględną różnicy liczb wyrzuconych oczek. Oblicz prawdopodobieństwo zdarzenia 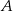 polegającego na tym, że obliczona wartość bezwzględna różnicy wyrzuconych oczek jest równa 3, 4 lub 5.
polegającego na tym, że obliczona wartość bezwzględna różnicy wyrzuconych oczek jest równa 3, 4 lub 5.
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo otrzymania iloczynu oczek równego 5.
Gracz rzuca dwukrotnie symetryczną sześcienną kostką do gry i oblicza sumę liczb wyrzuconych oczek. Oblicz prawdopodobieństwo zdarzenia 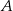 polegającego na tym, że suma liczb wyrzuconych oczek jest równa 4 lub 5, lub 6.
polegającego na tym, że suma liczb wyrzuconych oczek jest równa 4 lub 5, lub 6.
Rzucamy dwiema sześciennymi kostkami. Jakie jest prawdopodobieństwo, że co najmniej na jednej kostce będzie jedynka?
Rzucamy czerwoną i zieloną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na wyrzuceniu takiej samej liczby oczek na obu kostkach.
Rzucamy dwiema sześciennymi kostkami. Jakie jest prawdopodobieństwo, że na obu kostkach będzie ta sama liczba oczek?
Rzucamy dwiema sześciennymi kostkami. Jakie jest prawdopodobieństwo, że suma oczek będzie równa 4?
Rzucamy dwiema sześciennymi kostkami. Jakie jest prawdopodobieństwo, że na każdej kostce będzie co najmniej 5 oczek?
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia 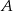 polegającego na tym, że liczba oczek w drugim rzucie jest o 1 większa od liczby oczek w pierwszym rzucie.
polegającego na tym, że liczba oczek w drugim rzucie jest o 1 większa od liczby oczek w pierwszym rzucie.
Rzucamy dwa razy kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w pierwszym rzucie wypadnie podzielna przez 3 liczba oczek.
Rzucamy dwukrotnie sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma liczb oczek otrzymanych na obu kostkach jest większa od 6 i iloczyn tych liczb jest nieparzysty.

