Wyznacz współczynniki 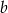 i
i  trójmianu kwadratowego
trójmianu kwadratowego 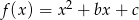 , wiedząc że jego miejsca zerowe
, wiedząc że jego miejsca zerowe 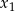 i
i 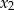 spełniają warunek:
spełniają warunek: 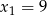 i
i 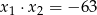 .
.
/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Równania z pierwiastkami
Dane jest równanie 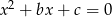 z niewiadomą
z niewiadomą  . Wyznacz wartości
. Wyznacz wartości 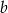 i
i  tak, by były one rozwiązaniami danego równania.
tak, by były one rozwiązaniami danego równania.
Punkt 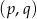 należy do zbioru
należy do zbioru 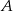 wtedy i tylko wtedy, gdy równanie
wtedy i tylko wtedy, gdy równanie 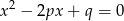 ma dwa różne rozwiązania
ma dwa różne rozwiązania 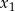 i
i 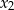 takie, że
takie, że 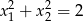 . Zaznacz w układzie współrzędnych zbiór
. Zaznacz w układzie współrzędnych zbiór 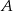 .
.
Oblicz wszystkie wartości parametru 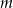 , dla których równanie
, dla których równanie 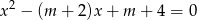 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 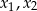 takie, że
takie, że 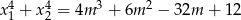 .
.
Dla jakich wartości parametru 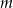 równanie
równanie 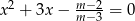 ma dwa pierwiastki rzeczywiste? Wyznacz te wartości parametru
ma dwa pierwiastki rzeczywiste? Wyznacz te wartości parametru 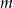 , dla których suma sześcianów pierwiastków tego równania jest równa -9.
, dla których suma sześcianów pierwiastków tego równania jest równa -9.
Dla jakich wartości parametru 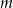 równanie
równanie 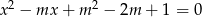 ma dwa różne pierwiastki rzeczywiste, których suma jest o jeden większa od ich iloczynu?
ma dwa różne pierwiastki rzeczywiste, których suma jest o jeden większa od ich iloczynu?
Dane jest równanie 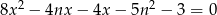 z niewiadomą
z niewiadomą  i parametrem
i parametrem  .
.
- Wyznacz wszystkie wartości
 , dla których suma odwrotności pierwiastków tego równania jest równa
, dla których suma odwrotności pierwiastków tego równania jest równa 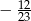 .
. - Wykaż, że jeżeli
 jest liczbą całkowitą, to suma kwadratów pierwiastków tego równania też jest liczbą całkowitą.
jest liczbą całkowitą, to suma kwadratów pierwiastków tego równania też jest liczbą całkowitą.
Dla jakich wartości parametru 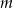 suma pierwiastków równania
suma pierwiastków równania 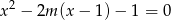 jest równa sumie kwadratów tych pierwiastków?
jest równa sumie kwadratów tych pierwiastków?
Wyznacz wszystkie liczby 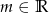 , dla których równanie
, dla których równanie 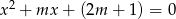 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 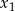 i
i 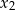 takie, że
takie, że 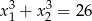 .
.
Oblicz wszystkie wartości parametru 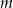 , dla których równanie
, dla których równanie 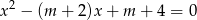 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 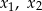 takie, że
takie, że 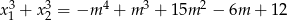 .
.
Wyznacz wszystkie liczby 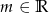 , dla których równanie
, dla których równanie 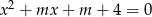 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 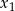 i
i 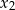 takie, że
takie, że 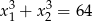 .
.
Liczby 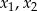 są takimi rozwiązaniami równania
są takimi rozwiązaniami równania 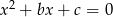
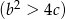 , że
, że 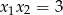 i
i 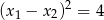 . Oblicz
. Oblicz 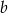 i
i  .
.
Dany jest trójmian kwadratowy 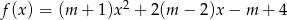 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 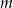 , dla których trójmian
, dla których trójmian 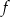 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 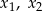 , spełniające warunek
, spełniające warunek 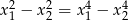 .
.
Dany jest trójmian kwadratowy 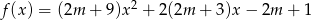 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 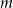 , dla których trójmian
, dla których trójmian 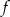 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 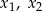 , spełniające warunek
, spełniające warunek 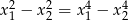 .
.
Wyznacz wszystkie wartości parametru 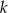 , dla których równanie
, dla których równanie
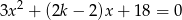
ma dwa różne rozwiązania rzeczywiste 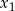 i
i 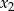 , przy czym
, przy czym 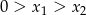 , spełniające warunek
, spełniające warunek
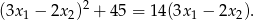
Wyznacz wszystkie wartości parametru 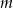 , dla których równanie
, dla których równanie 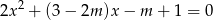 ma dwa różne pierwiastki
ma dwa różne pierwiastki 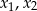 takie, że
takie, że 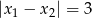 .
.
Wyznacz wszystkie wartości parametru 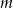 , dla których funkcja kwadratowa
, dla których funkcja kwadratowa 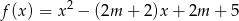 ma dwa różne pierwiastki
ma dwa różne pierwiastki 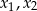 takie, że suma kwadratów odległości punktów
takie, że suma kwadratów odległości punktów 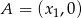 i
i 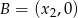 od prostej o równaniu
od prostej o równaniu 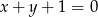 jest równa 6.
jest równa 6.
Liczby 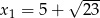 i
i 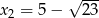 są rozwiązaniami równania
są rozwiązaniami równania 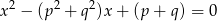 z niewiadomą
z niewiadomą  . Oblicz wartości
. Oblicz wartości 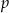 i
i 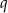 .
.
Wyznacz wszystkie wartości parametru 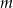 , dla których równanie
, dla których równanie 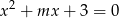 ma dwa różne pierwiastki rzeczywiste, takie, że suma ich czwartych potęg jest równa 82.
ma dwa różne pierwiastki rzeczywiste, takie, że suma ich czwartych potęg jest równa 82.
Wyznacz wszystkie wartości parametru 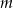 , dla których równanie
, dla których równanie 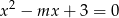 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 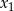 i
i 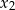 takie, że
takie, że 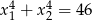 .
.
Wyznacz te wartości parametru 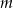 , dla których równanie
, dla których równanie 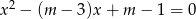 ma dwa rozwiązania
ma dwa rozwiązania 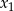 i
i 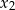 spełniające warunek
spełniające warunek 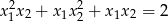 .
.
Dane jest równanie kwadratowe 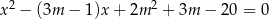 z niewiadomą
z niewiadomą  . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 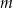 , dla których różne rozwiązania
, dla których różne rozwiązania 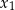 i
i 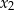 tego równania istnieją i spełniają warunek
tego równania istnieją i spełniają warunek
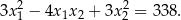
Dane jest równanie kwadratowe 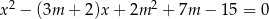 z niewiadomą
z niewiadomą  . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 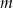 , dla których różne rozwiązania
, dla których różne rozwiązania 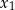 i
i 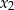 tego równania istnieją i spełniają warunek
tego równania istnieją i spełniają warunek
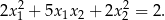
Wyznacz wszystkie wartości parametru 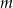 , dla których równanie
, dla których równanie 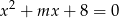 ma dwa różne pierwiastki rzeczywiste takie, że suma ich kwadratów jest równa
ma dwa różne pierwiastki rzeczywiste takie, że suma ich kwadratów jest równa 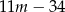 .
.
Wyznacz wszystkie wartości parametru 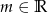 , dla których równanie
, dla których równanie 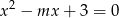 ma dwa różne pierwiastki
ma dwa różne pierwiastki 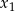 i
i 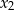 takie, że
takie, że 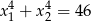 .
.
Dla jakiego parametru 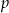 iloczyn miejsc zerowych funkcji
iloczyn miejsc zerowych funkcji 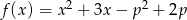 jest równy mniejszemu pierwiastkowi równania
jest równy mniejszemu pierwiastkowi równania 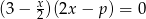 .
.

