Zestaw użytkownika nr 7772_3321
Zestaw użytkownika
nr 7772_3321
Wielomian 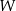 jest wielomianem stopnia 5 i spełnia warunki:
jest wielomianem stopnia 5 i spełnia warunki: 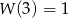 oraz
oraz 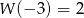 . Wykaż, że nie wszystkie współczynniki wielomianu
. Wykaż, że nie wszystkie współczynniki wielomianu 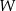 są liczbami całkowitymi.
są liczbami całkowitymi.
Wielomian 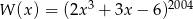 , po wykonaniu potęgowania i dokonaniu redukcji wyrazów podobnych, zapisano w postaci
, po wykonaniu potęgowania i dokonaniu redukcji wyrazów podobnych, zapisano w postaci 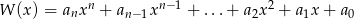 . Oblicz sumę
. Oblicz sumę 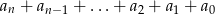 .
.
Wyznacz te argumenty, dla których funkcja 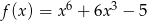 osiąga wartość najmniejszą.
osiąga wartość najmniejszą.
Uzasadnij, że dla każdej liczby naturalnej  wartość wielomianu
wartość wielomianu 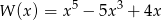 jest liczbą podzielną przez 120.
jest liczbą podzielną przez 120.
Wielomian 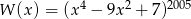 , po wykonaniu potęgowania i dokonaniu redukcji wyrazów podobnych, zapisano w postaci
, po wykonaniu potęgowania i dokonaniu redukcji wyrazów podobnych, zapisano w postaci 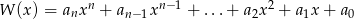 . Oblicz sumę
. Oblicz sumę 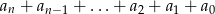 .
.
Dana jest funkcja 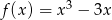 dla
dla 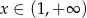 . Zbadaj na podstawie definicji monotoniczność tej funkcji w przedziale
. Zbadaj na podstawie definicji monotoniczność tej funkcji w przedziale 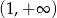 .
.
Dane są wielomiany 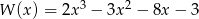 i
i 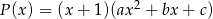 .
.
- Wyznacz współczynniki
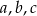 tak, aby
tak, aby 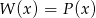 .
. - Przedstaw wielomian
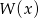 jako iloczyn wielomianów liniowych.
jako iloczyn wielomianów liniowych.
Dany jest wielomian 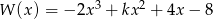 .
.
- Wyznacz wartość
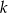 tak, aby reszta z dzielenia wielomianu W przez dwumian
tak, aby reszta z dzielenia wielomianu W przez dwumian 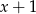 była równa -6.
była równa -6. - Dla znalezionej wartości
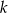 rozłóż wielomian na czynniki liniowe.
rozłóż wielomian na czynniki liniowe. - Dla znalezionej wartości
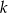 rozwiąż nierówność
rozwiąż nierówność 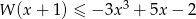 .
.
Wyznacz współczynniki 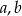 wielomianu
wielomianu 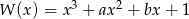 wiedząc, że dla każdego
wiedząc, że dla każdego 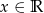 prawdziwa jest równość:
prawdziwa jest równość: 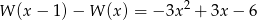 .
.
Wielomian 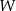 dany jest wzorem
dany jest wzorem 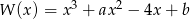 .
.
- Wyznacz
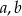 oraz
oraz  tak, aby wielomian
tak, aby wielomian 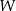 był równy wielomianowi
był równy wielomianowi 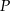 , gdy
, gdy 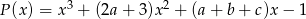 .
. - Dla
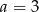 i
i 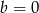 zapisz wielomian
zapisz wielomian 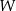 w postaci iloczynu trzech wielomianów stopnia pierwszego.
w postaci iloczynu trzech wielomianów stopnia pierwszego.
Rozłóż wielomian 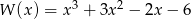 na czynniki liniowe.
na czynniki liniowe.
Korzystając z definicji funkcji rożnowartościowej wykaż, że funkcja 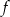 określona wzorem
określona wzorem 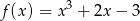 jest rożnowartościowa.
jest rożnowartościowa.
Wyznacz zbiór wartości funkcji 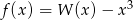 , gdzie
, gdzie 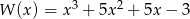 .
.
Dla każdej liczby rzeczywistej  obliczamy różnicę sześcianów liczb: o 1 mniejszej od
obliczamy różnicę sześcianów liczb: o 1 mniejszej od  oraz o 2 większej od
oraz o 2 większej od  . Zapisz wzór otrzymanej w ten sposób funkcji i wyznacz jej wartość największą.
. Zapisz wzór otrzymanej w ten sposób funkcji i wyznacz jej wartość największą.
Sprawdź, czy równe są wielomiany 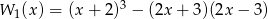 i
i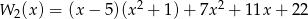 .
.
Dany jest wielomian 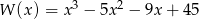 .
.
- Sprawdź, czy punkt
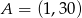 należy do wykresu tego wielomianu.
należy do wykresu tego wielomianu. - Zapisz wielomian
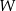 w postaci iloczynu trzech wielomianów stopnia pierwszego.
w postaci iloczynu trzech wielomianów stopnia pierwszego.
Dany jest wielomian 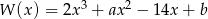 .
.
- Dla
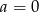 i
i 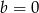 otrzymamy wielomian
otrzymamy wielomian 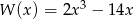 . Rozwiąż równanie
. Rozwiąż równanie 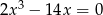 .
. - Dobierz wartości
 i
i 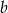 tak, aby wielomian
tak, aby wielomian 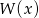 był podzielny jednocześnie przez
był podzielny jednocześnie przez 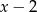 oraz
oraz 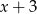 .
.
Wielomiany 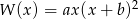 i
i 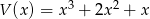 są równe. Oblicz
są równe. Oblicz  i
i 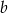 .
.
Dany jest wielomian 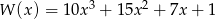 .
.
- Zapisz wielomian
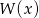 jako iloczyn wielomianów liniowych.
jako iloczyn wielomianów liniowych. - Określ dziedzinę funkcji
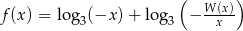 .
.
Wielomiany 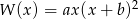 i
i 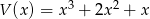 są równe. Oblicz
są równe. Oblicz  i
i 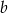 .
.
Sprawdź, czy równe są wielomiany 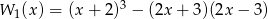 i
i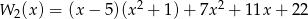 .
.
Dla każdej liczby rzeczywistej  obliczamy różnicę sześcianów liczb: o 1 mniejszej od
obliczamy różnicę sześcianów liczb: o 1 mniejszej od  oraz o 2 większej od
oraz o 2 większej od  . Zapisz wzór otrzymanej w ten sposób funkcji i wyznacz jej wartość największą.
. Zapisz wzór otrzymanej w ten sposób funkcji i wyznacz jej wartość największą.
Wyznacz zbiór wartości funkcji 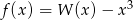 , gdzie
, gdzie 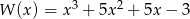 .
.
Korzystając z definicji funkcji rożnowartościowej wykaż, że funkcja 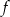 określona wzorem
określona wzorem 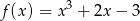 jest rożnowartościowa.
jest rożnowartościowa.
Dana jest funkcja 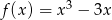 dla
dla 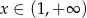 . Zbadaj na podstawie definicji monotoniczność tej funkcji w przedziale
. Zbadaj na podstawie definicji monotoniczność tej funkcji w przedziale 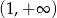 .
.
Dane są wielomiany 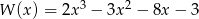 i
i 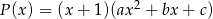 .
.
- Wyznacz współczynniki
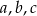 tak, aby
tak, aby 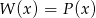 .
. - Przedstaw wielomian
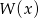 jako iloczyn wielomianów liniowych.
jako iloczyn wielomianów liniowych.
Dany jest wielomian 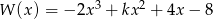 .
.
- Wyznacz wartość
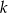 tak, aby reszta z dzielenia wielomianu W przez dwumian
tak, aby reszta z dzielenia wielomianu W przez dwumian 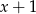 była równa -6.
była równa -6. - Dla znalezionej wartości
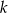 rozłóż wielomian na czynniki liniowe.
rozłóż wielomian na czynniki liniowe. - Dla znalezionej wartości
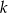 rozwiąż nierówność
rozwiąż nierówność 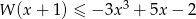 .
.
Wyznacz współczynniki 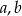 wielomianu
wielomianu 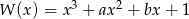 wiedząc, że dla każdego
wiedząc, że dla każdego 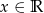 prawdziwa jest równość:
prawdziwa jest równość: 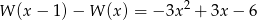 .
.
Wielomian 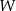 dany jest wzorem
dany jest wzorem 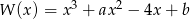 .
.
- Wyznacz
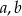 oraz
oraz  tak, aby wielomian
tak, aby wielomian 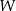 był równy wielomianowi
był równy wielomianowi 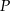 , gdy
, gdy 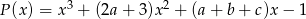 .
. - Dla
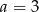 i
i 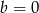 zapisz wielomian
zapisz wielomian 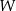 w postaci iloczynu trzech wielomianów stopnia pierwszego.
w postaci iloczynu trzech wielomianów stopnia pierwszego.
Dany jest wielomian 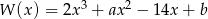 .
.
- Dla
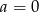 i
i 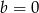 otrzymamy wielomian
otrzymamy wielomian 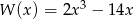 . Rozwiąż równanie
. Rozwiąż równanie 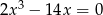 .
. - Dobierz wartości
 i
i 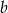 tak, aby wielomian
tak, aby wielomian 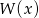 był podzielny jednocześnie przez
był podzielny jednocześnie przez 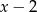 oraz
oraz 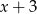 .
.
Przedstaw wielomian 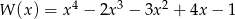 w postaci iloczynu dwóch wielomianów stopnia drugiego o współczynnikach całkowitych i takich, że współczynniki przy drugich potęgach są równe jeden.
w postaci iloczynu dwóch wielomianów stopnia drugiego o współczynnikach całkowitych i takich, że współczynniki przy drugich potęgach są równe jeden.

