Zadanie nr 3756900
Dany jest ostrosłup prawidłowy trójkątny 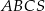 o podstawie
o podstawie 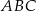 . Krawędź podstawy tego ostrosłupa ma długość
. Krawędź podstawy tego ostrosłupa ma długość  . Ściana boczna jest nachylona do płaszczyzny podstawy pod kątem
. Ściana boczna jest nachylona do płaszczyzny podstawy pod kątem  takim, że
takim, że 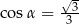 . Przez środek
. Przez środek 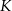 krawędzi
krawędzi 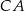 i środek
i środek 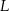 krawędzi
krawędzi 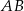 poprowadzono płaszczyznę
poprowadzono płaszczyznę 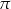 prostopadłą do płaszczyzny
prostopadłą do płaszczyzny 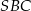 . Oblicz pole otrzymanego przekroju.
. Oblicz pole otrzymanego przekroju.
Rozwiązanie
Szkicujemy opisaną sytuację.
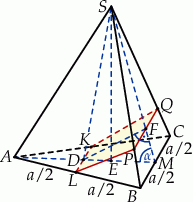
Otrzymany przekrój to oczywiście trapez o podstawach
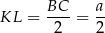
i 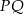 . Z obliczeniem długości tej drugiej podstawy będzie trochę więcej zachodu – widać, że przyda się do tego podobieństwo trójkątów
. Z obliczeniem długości tej drugiej podstawy będzie trochę więcej zachodu – widać, że przyda się do tego podobieństwo trójkątów 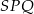 i
i 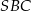 . Musimy też obliczyć wysokość
. Musimy też obliczyć wysokość 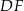 trapezu i może od tego zacznijmy. Odcinek
trapezu i może od tego zacznijmy. Odcinek 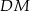 to połowa wysokości trójkąta równobocznego
to połowa wysokości trójkąta równobocznego 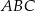 , więc
, więc
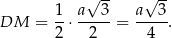
Patrzymy teraz na trójkąt prostokątny 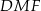 .
.
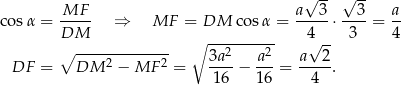
Pozostało więc obliczyć długość podstawy 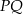 trapezu
trapezu 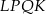 . Jak już wcześniej zauważyliśmy, zrobimy to korzystając z podobieństwa trójkątów
. Jak już wcześniej zauważyliśmy, zrobimy to korzystając z podobieństwa trójkątów 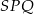 i
i 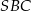 , ale zanim będziemy mogli to zrobić, obliczmy długość odcinka
, ale zanim będziemy mogli to zrobić, obliczmy długość odcinka 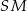 . Patrzymy na trójkąt prostokątny
. Patrzymy na trójkąt prostokątny 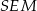 .
.
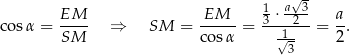
Tak naprawdę w tym miejscu okazało się, że trójkąt 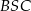 jest połówka kwadratu z kątem prostym przy wierzchołku
jest połówka kwadratu z kątem prostym przy wierzchołku 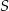 , ale mniejsza o to – w tym momencie nie ma to już wielkiego wpływu na dalsze rozwiązanie. Patrzymy teraz na trójkąty podobne
, ale mniejsza o to – w tym momencie nie ma to już wielkiego wpływu na dalsze rozwiązanie. Patrzymy teraz na trójkąty podobne 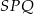 i
i 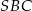 .
.
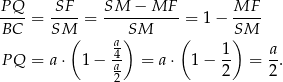
Obliczamy pole trapezu 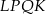 (który okazał się być prostokątem).
(który okazał się być prostokątem).
Odpowiedź: 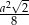 .
.

