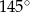Punkty  dzielą okrąg na 5 równych łuków. Miara zaznaczonego na rysunku kąta wpisanego
dzielą okrąg na 5 równych łuków. Miara zaznaczonego na rysunku kąta wpisanego  jest równa
jest równa
A) 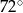 B)
B) 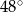 C)
C) 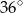 D)
D) 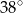
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Punkty 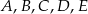 dzielą okrąg na 5 równych łuków. Miara zaznaczonego na rysunku kąta wpisanego
dzielą okrąg na 5 równych łuków. Miara zaznaczonego na rysunku kąta wpisanego 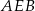 jest równa
jest równa

A) 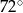 B)
B) 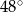 C)
C) 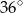 D)
D) 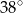
Punkty 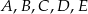 okręgu są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego
okręgu są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego 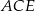 jest równa
jest równa
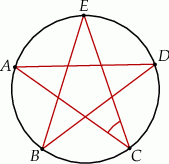
A) 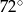 B)
B) 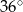 C)
C) 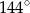 D)
D) 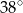
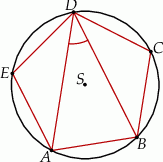
Punkty 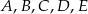 leżące na okręgu o środku
leżące na okręgu o środku 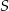 są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego
są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego 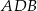 jest równa
jest równa
A) 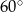 B)
B) 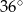 C)
C) 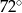 D)
D) 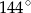
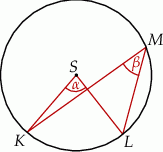
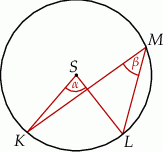
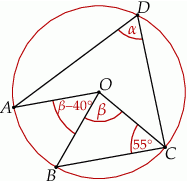
Punkty 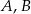 i
i 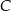 leżą na okręgu o środku
leżą na okręgu o środku 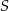 (zobacz rysunek).
(zobacz rysunek).
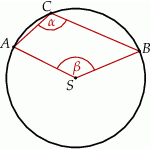
Miary  i
i 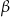 zaznaczonych kątów
zaznaczonych kątów 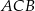 i
i 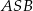 spełniają warunek
spełniają warunek 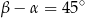 . Wynika stąd, że
. Wynika stąd, że
A) 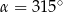 B)
B) 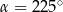 C)
C) 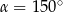 D)
D) 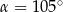
Cięciwa dzieli okrąg na dwa łuki w stosunku 5:7. Miara kąta wpisanego opartego na krótszym łuku okręgu jest równa
A) 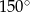 B)
B) 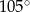 C)
C) 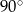 D)
D) 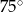
Średnice 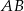 i
i 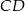 okręgu o środku
okręgu o środku 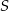 przecinają się pod kątem
przecinają się pod kątem 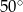 (tak jak na rysunku).
(tak jak na rysunku).
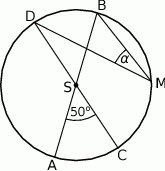
Miara kąta  jest równa
jest równa
A) 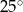 B)
B) 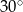 C)
C) 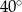 D)
D) 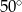
Średnice 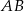 i
i 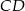 okręgu o środku
okręgu o środku 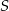 przecinają się pod kątem
przecinają się pod kątem 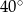 (tak jak na rysunku).
(tak jak na rysunku).
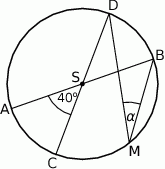
Miara kąta  jest równa
jest równa
A) 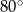 B)
B) 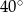 C)
C) 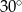 D)
D) 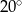
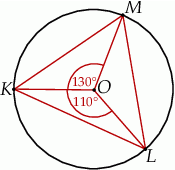
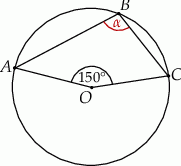
Punkt 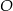 jest środkiem okręgu (zobacz rysunek). Miara kąta
jest środkiem okręgu (zobacz rysunek). Miara kąta  jest równa
jest równa
A) 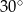 B)
B) 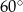 C)
C) 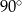 D)
D) 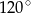
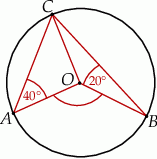
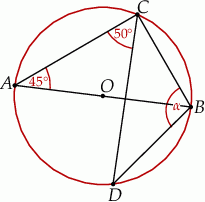
Punkty 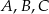 leżą na okręgu o środku
leżą na okręgu o środku 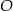 (zobacz rysunek). Ponadto
(zobacz rysunek). Ponadto 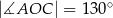 oraz
oraz  .
.
Miara kąta wewnętrznego  trójkąta
trójkąta 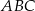 jest równa
jest równa
A) 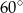 B)
B) 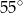 C)
C) 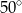 D)
D) 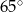
Punkty 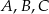 leżą na okręgu o środku
leżą na okręgu o środku 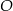 (zobacz rysunek). Ponadto
(zobacz rysunek). Ponadto 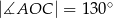 oraz
oraz 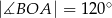 .
.
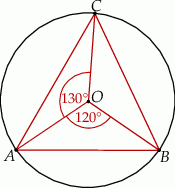
Miara kąta wewnętrznego 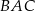 trójkąta
trójkąta 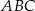 jest równa
jest równa
A) 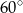 B)
B) 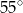 C)
C) 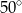 D)
D) 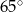
Punkty 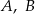 i
i 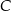 leżą na okręgu o środku
leżą na okręgu o środku 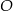 (zobacz rysunek). Zaznaczony na rysunku wypukły kąt środkowy
(zobacz rysunek). Zaznaczony na rysunku wypukły kąt środkowy 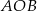 ma miarę
ma miarę
A) 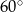 B)
B) 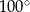 C)
C) 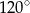 D)
D) 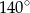
Punkt  jest środkiem okręgu (rysunek).
jest środkiem okręgu (rysunek).
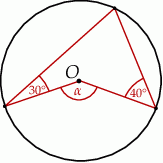
Miara kąta  jest równa
jest równa
A) 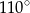 B)
B) 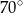 C)
C) 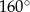 D)
D) 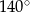
Punkt O jest środkiem okręgu (rysunek).
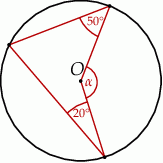
Miara kąta  jest równa
jest równa
A) 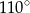 B)
B) 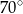 C)
C) 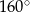 D)
D) 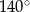
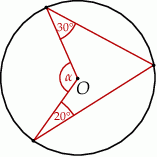
Punkt  jest środkiem okręgu. Kąt środkowy
jest środkiem okręgu. Kąt środkowy  ma miarę
ma miarę
A) 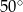 B)
B) 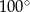 C)
C) 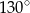 D)
D) 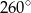
Na okręgu o środku w punkcie 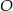 leżą punkty
leżą punkty 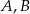 i
i 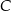 (zobacz rysunek). Kąt
(zobacz rysunek). Kąt  ma miarę
ma miarę 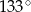 , a kąt
, a kąt 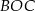 ma miarę
ma miarę 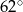 .
.
Kąt  ma miarę
ma miarę
A) 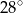 B)
B) 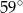 C)
C) 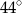 D)
D) 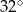
Na okręgu o środku w punkcie 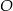 leżą punkty
leżą punkty 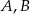 i
i 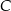 (zobacz rysunek). Kąt
(zobacz rysunek). Kąt 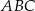 ma miarę
ma miarę 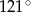 , a kąt
, a kąt 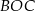 ma miarę
ma miarę 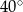 .
.
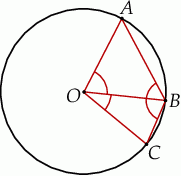
Kąt 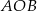 ma miarę
ma miarę
A) 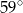 B)
B) 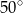 C)
C) 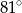 D)
D) 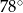
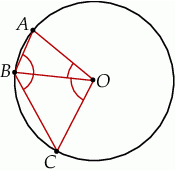
Punkty 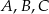 leżą na okręgu o środku
leżą na okręgu o środku  (rysunek),
(rysunek), 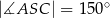 oraz
oraz 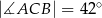 . Miara kąta
. Miara kąta 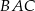 jest równa
jest równa
A) 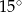 B)
B) 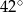 C)
C) 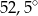 D)
D) 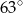
Na okręgu o środku w punkcie 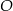 leżą punkty
leżą punkty 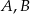 i
i 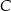 (zobacz rysunek). Kąt
(zobacz rysunek). Kąt 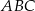 ma miarę
ma miarę 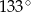 , a kąt
, a kąt 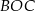 ma miarę
ma miarę 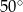 .
.
Kąt  ma miarę
ma miarę
A) 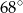 B)
B) 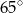 C)
C) 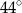 D)
D) 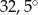
Odcinek 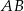 jest średnicą okręgu o środku
jest średnicą okręgu o środku  .
.
Miara kąta  oznaczonego na rysunku literą
oznaczonego na rysunku literą  jest równa
jest równa
A)  B)
B) 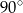 C)
C) 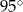 D)
D) 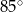
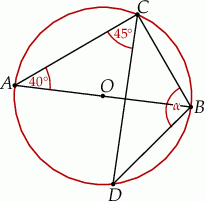
Punkty 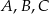 i
i 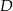 leżą na okręgu o środku
leżą na okręgu o środku 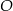 . Punkt
. Punkt 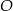 leży na odcinku
leży na odcinku 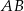 oraz
oraz 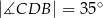 ,
, 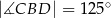 .
.
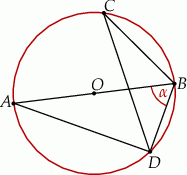
Miara kąta 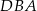 oznaczonego na rysunku literą
oznaczonego na rysunku literą  jest równa
jest równa
A) 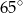 B)
B) 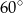 C)
C) 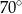 D)
D) 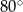
Odcinek 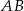 jest średnicą okręgu o środku
jest średnicą okręgu o środku  .
.
Miara kąta  oznaczonego na rysunku literą
oznaczonego na rysunku literą  jest równa
jest równa
A) 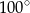 B)
B) 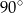 C)
C) 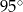 D)
D) 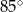
Dany jest okrąg o środku 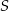 . Punkty
. Punkty 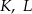 i
i 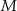 leżą na tym okręgu. Na łuku
leżą na tym okręgu. Na łuku 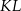 tego okręgu są oparte kąty
tego okręgu są oparte kąty 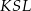 i
i 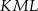 (zobacz rysunek), których miary
(zobacz rysunek), których miary  i
i 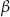 spełniają warunek
spełniają warunek 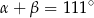 . Wynika stąd, że
. Wynika stąd, że
A)  B)
B)  C)
C)  D)
D) 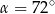
Dany jest okrąg o środku 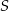 . Punkty
. Punkty 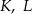 i
i 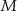 leżą na tym okręgu. Na łuku
leżą na tym okręgu. Na łuku 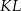 tego okręgu są oparte kąty
tego okręgu są oparte kąty 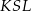 i
i 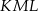 (zobacz rysunek), których miary
(zobacz rysunek), których miary  i
i 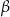 spełniają warunek
spełniają warunek 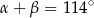 . Wynika stąd, że
. Wynika stąd, że
A) 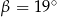 B)
B) 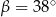 C)
C) 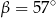 D)
D) 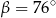
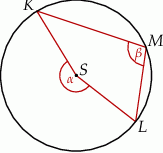
Dany jest okrąg o środku 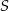 . Punkty
. Punkty 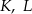 i
i 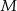 leżą na tym okręgu. Na łuku
leżą na tym okręgu. Na łuku 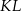 tego okręgu są oparte kąty
tego okręgu są oparte kąty 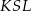 i
i 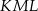 (zobacz rysunek), których miary
(zobacz rysunek), których miary  i
i 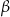 spełniają warunek
spełniają warunek 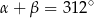 . Wynika stąd, że
. Wynika stąd, że
A) 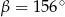 B)
B) 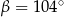 C)
C) 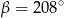 D)
D) 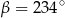
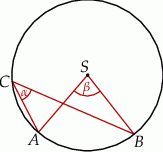
Dany jest okrąg o środku 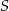 . Punkty
. Punkty 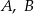 i
i 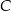 leżą na tym okręgu. Na łuku
leżą na tym okręgu. Na łuku 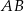 tego okręgu są oparte kąty
tego okręgu są oparte kąty 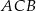 i
i 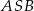 (zobacz rysunek), których miary
(zobacz rysunek), których miary  i
i 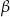 spełniają warunek
spełniają warunek 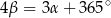 . Wynika stąd, że
. Wynika stąd, że
A) 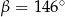 B)
B) 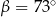 C)
C) 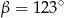 D)
D) 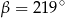
Miara kąta wpisanego opartego na tym samym łuku co kąt środkowy o mierze 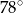 jest równa
jest równa
A) 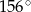 B)
B) 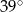 C)
C) 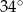 D)
D) 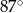
Miara kąta wpisanego opartego na tym samym łuku co kąt środkowy o mierze 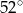 jest równa
jest równa
A) 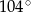 B)
B) 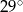 C)
C) 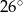 D)
D) 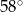
Na poniższym rysunku punkt  jest środkiem okręgu.
jest środkiem okręgu.
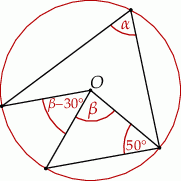
Miara kąta  jest równa
jest równa
A) 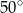 B)
B) 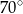 C)
C) 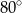 D)
D) 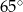
Na poniższym rysunku punkt  jest środkiem okręgu.
jest środkiem okręgu.
Miara kąta  jest równa
jest równa
A) 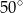 B)
B) 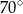 C)
C) 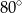 D)
D) 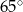
Trójkąt 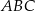 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 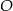 . Jeśli
. Jeśli 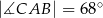 i
i  jest średnicą okręgu, to miara kąta
jest średnicą okręgu, to miara kąta  jest równa
jest równa
A)  B)
B) 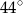 C)
C) 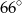 D)
D) 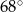
Kąt 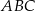 (patrz rysunek) ma miarę
(patrz rysunek) ma miarę
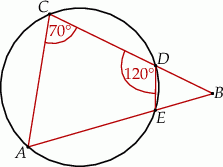
A)  B)
B)  C)
C)  D)
D) 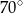
Na łukach 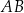 i
i 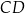 okręgu są oparte kąty wpisane
okręgu są oparte kąty wpisane 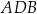 i
i  , takie, że
, takie, że  i
i  (zobacz rysunek). Cięciwy
(zobacz rysunek). Cięciwy  i
i 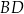 przecinają się w punkcie
przecinają się w punkcie 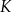 .
.

Miara kąta 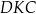 jest równa
jest równa
A) 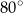 B)
B) 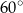 C)
C) 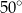 D)
D) 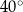
Wierzchołki  czworokąta
czworokąta 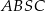 leżą na okręgu o środku
leżą na okręgu o środku 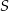 . Kąt
. Kąt 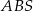 ma miarę
ma miarę 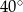 (zobacz rysunek), a przekątna
(zobacz rysunek), a przekątna 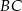 jest dwusieczną tego kąta.
jest dwusieczną tego kąta.
Miara kąta  jest równa
jest równa
A)  B)
B) 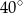 C)
C) 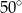 D)
D) 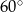
Suma miar kąta wpisanego i kąta środkowego, opartych na 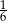 okręgu, jest równa
okręgu, jest równa
A) 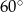 B)
B) 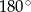 C)
C) 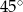 D)
D) 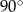
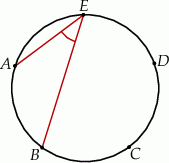
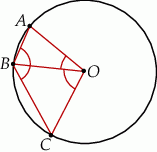
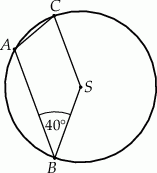
Punkty  i
i  leżą na okręgu o środku
leżą na okręgu o środku  (zobacz rysunek).
(zobacz rysunek).
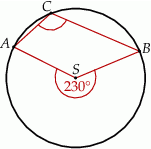
Miara zaznaczonego kąta wpisanego 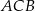 jest równa
jest równa
A) 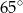 B)
B) 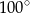 C)
C) 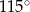 D)
D) 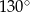
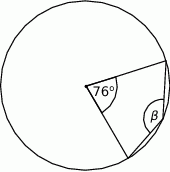
Miara kąta 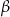 zaznaczonego na rysunku obok jest równa:
zaznaczonego na rysunku obok jest równa:
A) 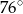 B)
B) 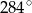 C)
C) 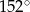 D)
D) 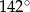
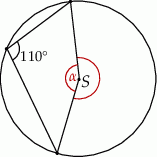
Punkt  jest środkiem koła. Zatem miara kąta
jest środkiem koła. Zatem miara kąta  jest równa
jest równa
A) 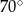 B)
B) 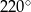 C)
C) 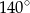 D)
D) 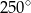
Punkty 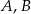 i
i 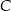 leżą na okręgu o środku
leżą na okręgu o środku 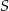 (zobacz rysunek).
(zobacz rysunek).
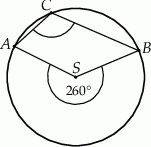
Miara zaznaczonego kąta wpisanego 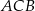 jest równa
jest równa
A) 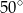 B)
B) 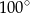 C)
C) 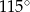 D)
D) 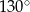
Punkty 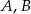 i
i 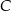 leżą na okręgu o środku
leżą na okręgu o środku 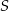 (zobacz rysunek).
(zobacz rysunek).
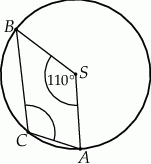
Miara zaznaczonego kąta wpisanego 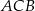 jest równa
jest równa
A) 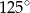 B)
B) 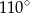 C)
C) 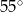 D)
D) 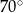
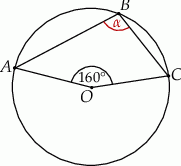
Punkt 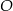 jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany  ma miarę
ma miarę
A) 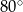 B)
B) 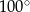 C)
C) 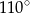 D)
D) 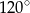
Punkt  jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany  ma miarę
ma miarę
A) 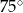 B)
B) 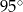 C)
C) 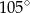 D)
D) 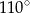
W okręgu o środku 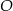 dany jest kąt o mierze
dany jest kąt o mierze 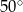 , zaznaczony na rysunku.
, zaznaczony na rysunku.
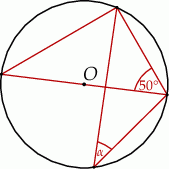
Miara kąta oznaczonego na rysunku literą  jest równa
jest równa
A) 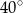 B)
B) 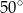 C)
C) 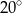 D)
D) 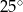
W okręgu o środku 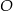 dany jest kąt o mierze
dany jest kąt o mierze 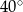 , zaznaczony na rysunku.
, zaznaczony na rysunku.
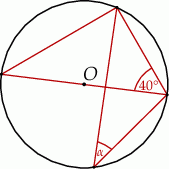
Miara kąta oznaczonego na rysunku literą  jest równa
jest równa
A) 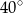 B)
B) 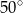 C)
C) 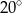 D)
D) 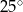
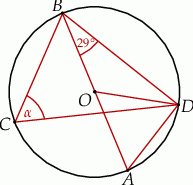
Dany jest kąt 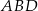 o mierze
o mierze 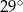 (rys.). Kąt
(rys.). Kąt 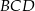 ma miarę:
ma miarę:
A) 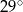 B)
B) 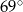 C)
C) 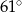 D)
D) 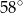
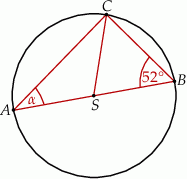
Miara kąta  trójkąta
trójkąta  wpisanego w okrąg o środku
wpisanego w okrąg o środku  jest równa
jest równa
A) 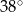 B)
B) 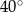 C)
C) 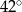 D)
D) 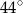
Na rysunku poniżej punkt 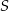 jest środkiem okręgu i miara kąt
jest środkiem okręgu i miara kąt 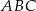 wynosi
wynosi 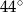 . Ile stopni ma kąt
. Ile stopni ma kąt 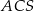 ?
?
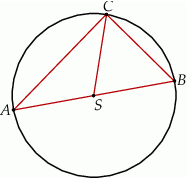
A) 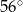 B)
B) 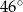 C)
C) 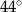 D)
D) 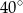
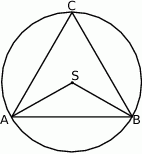
Jeżeli punkty 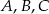 leżące na okręgu o środku
leżące na okręgu o środku 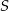 są wierzchołkami trójkąta równobocznego, to miara kąta środkowego
są wierzchołkami trójkąta równobocznego, to miara kąta środkowego 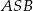 jest równa
jest równa
A) 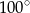 B)
B) 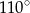 C)
C) 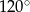 D)
D) 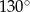
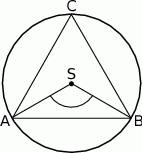
Punkty 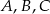 leżące na okręgu o środku
leżące na okręgu o środku 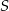 są wierzchołkami trójkąta równobocznego. Miara zaznaczonego na rysunku kąta środkowego
są wierzchołkami trójkąta równobocznego. Miara zaznaczonego na rysunku kąta środkowego 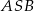 jest równa
jest równa
A) 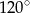 B)
B) 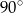 C)
C) 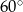 D)
D) 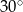
Punkty 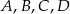 dzielą okrąg o środku
dzielą okrąg o środku 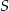 w stosunku
w stosunku 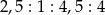 .
.
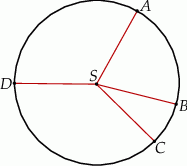
Różnica miar kątów wypukłych  i
i  jest równa
jest równa
A)  B)
B) 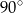 C)
C) 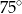 D)
D) 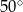
Na okręgu opisanym na kwadracie 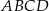 wybrano punkt
wybrano punkt 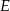 w ten sposób, że
w ten sposób, że 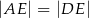 .
.
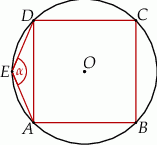
Miara kąta oznaczonego na rysunku literą  jest równa
jest równa
A) 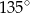 B)
B) 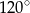 C)
C) 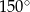 D)
D)