Pan Jakub ma 4 marynarki, 7 par różnych spodni i 10 różnych koszul. Na ile różnych sposobów może się ubrać, jeśli zawsze zakłada marynarkę, spodnie i koszulę.
A) 280 B) 21 C) 28 D) 70
/Szkoła średnia/Zadania testowe/Kombinatoryka
Pan Tomasz ma 5 marynarek, 9 par różnych spodni i 6 różnych koszul. Na ile różnych sposobów może się ubrać, jeśli zawsze zakłada marynarkę, spodnie i koszulę.
A) 20 B) 45 C) 280 D) 270
Pan Jakub ma 8 marynarek, 5 par różnych spodni i 9 różnych koszul. Na ile różnych sposobów może się ubrać, jeśli zawsze zakłada marynarkę, spodnie i koszulę.
A) 240 B) 22 C) 360 D) 90
Pan Łukasz ma 3 marynarki, 8 par różnych spodni i 11 różnych koszul. Na ile różnych sposobów może się ubrać, jeśli zawsze zakłada marynarkę, spodnie i koszulę.
A) 280 B) 22 C) 132 D) 264
Wyrażenie 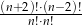 dla liczby naturalnej
dla liczby naturalnej 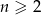 jest równe
jest równe
A) 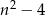 B)
B) 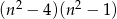 C)
C) 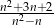 D)
D) 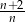
Wyrażenie 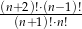 dla liczby naturalnej
dla liczby naturalnej 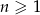 jest równe
jest równe
A) 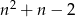 B)
B) 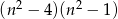 C)
C) 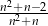 D)
D) 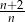
Flagę, taką jak pokazano na rysunku, należy zszyć z trzech jednakowej szerokości pasów kolorowej tkaniny. Oba pasy zewnętrzne mają być tego samego koloru, a pas znajdujący się między nimi ma być innego koloru. Liczba różnych takich flag, które można uszyć, mając do dyspozycji tkaniny w 10 kolorach, jest równa

A) 100 B) 99 C) 90 D) 19
Każdą z sześciu krawędzi sześciokątnej ramki postanowiono pomalować na jeden z 10 kolorów, przy czym przeciwległe krawędzie mają mieć ten sam kolor, a żadne dwie sąsiednie krawędzie nie mogą mieć tego samego koloru. Liczba różnych możliwości pokolorowania ramki jest równa

A) 720 B) 1000 C) 30 D) 27
Flagę, taką jak pokazano na rysunku, należy zszyć z trzech jednakowej szerokości pasów kolorowej tkaniny. Oba pasy zewnętrzne mają być tego samego koloru, a pas znajdujący się między nimi ma być innego koloru. Liczba różnych takich flag, które można uszyć, mając do dyspozycji tkaniny w 11 kolorach, jest równa

A) 121 B) 110 C) 90 D) 21
Ile różnych wyrazów z sensem lub bez sensu można ułożyć z liter wyrazu: MATEMATYKA?
A) 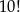 B) 30240 C) 151200 D)
B) 30240 C) 151200 D) 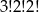
Ile jest wszystkich liczb pięciocyfrowych, większych 43080, utworzonych wyłącznie z cyfr 1, 2, 3, 4 przy założeniu, że cyfry mogą się powtarzać, ale nie wszystkie z tych cyfr muszą być wykorzystane?
A) 48 B) 15 C) 128 D) 192
Ile jest wszystkich liczb pięciocyfrowych, większych 53079, utworzonych wyłącznie z cyfr 2, 3, 4, 5 przy założeniu, że cyfry mogą się powtarzać, ale nie wszystkie z tych cyfr muszą być wykorzystane?
A) 48 B) 15 C) 128 D) 192
Z cyfr 1, 2, 3, 4, 5, 6 tworzymy sześciocyfrowe liczby o niepowtarzających się cyfrach w taki sposób, że cyfry parzyste zapisane są obok siebie. Powstało w ten sposób
A) 36 liczb B) 132 liczby C) 144 liczby D) 720 liczb
Pan Eugeniusz szykując się rano do pracy wybiera jeden spośród swoich 12 zegarków oraz dwa spośród 22 wiecznych piór, przy czym jedno z nich traktuje jako pióro zapasowe. Na ile sposobów może wybrać zestaw składający się z zegarka i dwóch piór, głównego i zapasowego?
A) 2777 B) 34 C) 5544 D) 5808
Pan Henryk szykując się rano do pracy wybiera jeden spośród swoich 10 zegarków oraz dwa spośród 18 wiecznych piór, przy czym jedno z nich traktuje jako pióro zapasowe. Na ile sposobów może wybrać zestaw składający się z zegarka i dwóch piór, głównego i zapasowego?
A) 45 B) 46 C) 3240 D) 3060
Ile jest liczb naturalnych pięciocyfrowych, których iloczyn cyfr jest równy 70?
A) 60 B) 36 C) 12 D) 125
W pewnym mieście na czas festynu postanowiono rozstawić stragany. Ustalono, że będzie można ustawić po 3 stragany po każdej stronie drogi. Na ile sposobów można ustawić te stragany?
A) 6 B) 24 C) 36 D) 720
W trakcie zawodów sportowych ośmioro uczniów miało ustawić się w dwóch rzędach po 4 osoby. Na ile sposobów mogą ustawić się ci uczniowie?
A) 4 B) 576 C) 40320 D) 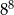
Dany jest zbiór trzynastu liczb 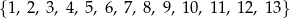 , z którego losujemy jednocześnie dwie liczby. Wszystkich różnych sposobów wylosowania z tego zbioru dwóch liczb, których iloczyn jest liczbą parzystą, jest
, z którego losujemy jednocześnie dwie liczby. Wszystkich różnych sposobów wylosowania z tego zbioru dwóch liczb, których iloczyn jest liczbą parzystą, jest
A) 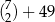 B)
B) 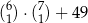 C)
C) 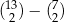 D)
D) 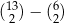
Ile jest liczb naturalnych dwucyfrowych większych od 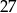 , które mają dwie różne cyfry?
, które mają dwie różne cyfry?
A) 63 B) 72 C) 65 D) 18
Ile jest liczb naturalnych dwucyfrowych mniejszych od 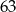 , które mają dwie różne cyfry?
, które mają dwie różne cyfry?
A) 45 B) 48 C) 63 D) 58
Ile jest liczb naturalnych trzycyfrowych większych od 694, które mają trzy różne cyfry?
A) 216 B) 219 C) 221 D) 246
Ile jest wszystkich dwucyfrowych liczb naturalnych podzielnych przez 3?
A) 12 B) 24 C) 29 D) 30
Ile jest wszystkich dwucyfrowych liczb naturalnych podzielnych przez 4?
A) 21 B) 22 C) 23 D) 24
Liczb naturalnych dwucyfrowych podzielnych przez 6 jest
A) 60 B) 45 C) 30 D) 15
Ile jest nieujemnych liczb całkowitych mniejszych niż 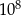 , które są zapisane wyłącznie przy użyciu cyfr 0, 1 i 2?
, które są zapisane wyłącznie przy użyciu cyfr 0, 1 i 2?
A) 19683 B) 59049 C) 6561 D) 512
Ile jest wszystkich liczb naturalnych dwucyfrowych, w których obie cyfry są parzyste?
A) 16 B) 20 C) 24 D) 25
Wszystkich liczb dwucyfrowych o różnych cyfrach jest
A) 90 B) 81 C) 82 D) 80
Ile jest wszystkich liczb naturalnych dwucyfrowych, w których obie cyfry są nieparzyste?
A) 16 B) 20 C) 24 D) 25
Liczb dwucyfrowych większych od 50 o nieparzystych cyfrach jest
A) 12 B) 25 C) 49 D) 15
Ile jest wszystkich liczb naturalnych dwucyfrowych, w których pierwsza cyfra jest parzysta, a druga nieparzysta?
A) 16 B) 20 C) 24 D) 25
Ile jest liczb naturalnych pięciocyfrowych, w których iloczyn cyfr jest równy 0?
A) 59049 B) 30951 C) 3439 D) 6561
Wszystkich liczb naturalnych dwucyfrowych, których obie cyfry są mniejsze od 5 jest
A) 16 B) 20 C) 25 D) 30
Ze zbioru 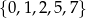 losujemy jedną liczbę, zapisujemy ją, a następnie bez zwracania losujemy i zapisujemy drugą. Ile w ten sposób otrzymamy liczb dwucyfrowych?
losujemy jedną liczbę, zapisujemy ją, a następnie bez zwracania losujemy i zapisujemy drugą. Ile w ten sposób otrzymamy liczb dwucyfrowych?
A) 20 B) 16 C) 12 D) 10
Wszystkich liczb naturalnych dwucyfrowych, których obie cyfry są mniejsze od 5 jest
A) 17 B) 18 C) 19 D) 20
Wszystkich liczb naturalnych dwucyfrowych, których obie cyfry są większe od 4 jest
A) 16 B) 20 C) 25 D) 30
Liczba 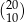 jest podzielna przez
jest podzielna przez
A) 5 B) 33 C) 221 D) 51
Liczba 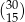 jest podzielna przez
jest podzielna przez
A) 7 B) 55 C) 143 D) 85
Ośmiu znajomych, wśród których jest jedno małżeństwo, kupiło bilety do kina na kolejne miejsca w jednym rzędzie (w rzędzie było dokładnie 8 miejsc). Wszystkich możliwych sposobów zajęcia miejsc tak, aby małżonkowie siedzieli obok siebie, jest:
A) 40320 B) 5040 C) 10080 D) 720
Pięć osób: Asia, Marta, Agnieszka, Edyta i Piotrek wybrało się do kina. Na ile sposobów mogą te osoby usiąść w jednym rzędzie na pięciu kolejnych miejscach tak, żeby Agnieszka i Piotrek siedzieli obok siebie?
A) 48 B) 36 C) 24 D) 12
Pięć osób: Wojtek, Marta, Agnieszka, Edyta i Piotrek wybrało się do kina. Na ile sposobów mogą te osoby usiąść w jednym rzędzie na pięciu kolejnych miejscach tak, żeby Piotrek siedział pomiędzy Agnieszką i Edytą?
A) 48 B) 36 C) 24 D) 12
Pięć osób: Arek, Marta, Agnieszka, Edyta i Piotrek wybrało się do kina. Na ile sposobów mogą te osoby usiąść w jednym rzędzie na pięciu kolejnych miejscach tak, żeby Agnieszkę i Piotrka rozdzielała jedna osoba?
A) 48 B) 36 C) 24 D) 12
Wszystkich liczb naturalnych trzycyfrowych parzystych, w których cyfra 7 występuje dokładnie jeden raz, jest
A) 85 B) 90 C) 100 D) 150
Ile jest wszystkich czterocyfrowych liczb naturalnych podzielnych przez 3?
A) 3000 B) 3333 C) 2999 D) 2998
Ile jest wszystkich czterocyfrowych liczb naturalnych podzielnych przez 7?
A) 1285 B) 1428 C) 1284 D) 1286
Ile jest wszystkich liczb naturalnych czterocyfrowych mniejszych od 2021 i podzielnych przez 3?
A) 673 B) 334 C) 340 D) 339
Ile jest wszystkich liczb naturalnych czterocyfrowych mniejszych od 2018 i podzielnych przez 5?
A) 402 B) 403 C) 203 D) 204
Ile jest wszystkich liczb naturalnych czterocyfrowych podzielnych przez 5?
A) 2000 B) 1800 C) 1000 D) 900
Ile jest wszystkich liczb naturalnych trzycyfrowych podzielnych przez 5?
A) 90 B) 100 C) 180 D) 200
Ile jest wszystkich pięciocyfrowych liczb naturalnych podzielnych przez 29?
A) 3103 B) 3105 C) 3104 D) 3106
Ile jest wszystkich liczb naturalnych czterocyfrowych mniejszych od 2020 i podzielnych przez 4?
A) 506 B) 505 C) 256 D) 255
Ile jest wszystkich czterocyfrowych liczb naturalnych podzielnych przez 13?
A) 692 B) 691 C) 690 D) 693
Ile jest wszystkich liczb naturalnych czterocyfrowych mniejszych od 2019 i podzielnych przez 4?
A) 256 B) 257 C) 255 D) 128

