Niech  będzie liczbą naturalną. Ze zbioru liczb
będzie liczbą naturalną. Ze zbioru liczb 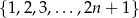 losujemy dwie liczby (mogą być równe). Oblicz prawdopodobieństwo, że suma wylosowanych liczb będzie większa od
losujemy dwie liczby (mogą być równe). Oblicz prawdopodobieństwo, że suma wylosowanych liczb będzie większa od 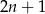 .
.
/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb
Ze zbioru wszystkich liczb trzycyfrowych losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 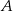 polegającego na wylosowaniu liczb, których iloczyn jest liczbą nieparzystą.
polegającego na wylosowaniu liczb, których iloczyn jest liczbą nieparzystą.
W zbiorze 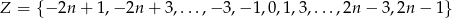 , gdzie
, gdzie 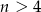 jest liczbą naturalną, zmieniono znaki na przeciwne trzem losowo wybranym liczbom. Wiadomo, że prawdopodobieństwo tego, że suma wszystkich liczb w zbiorze nie uległa zmianie wynosi
jest liczbą naturalną, zmieniono znaki na przeciwne trzem losowo wybranym liczbom. Wiadomo, że prawdopodobieństwo tego, że suma wszystkich liczb w zbiorze nie uległa zmianie wynosi 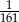 . Wyznacz
. Wyznacz  .
.
Ze zbioru liczb 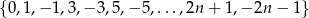 , gdzie
, gdzie  jest ustaloną liczbą naturalną, większą od 4, losujemy jednocześnie trzy liczby. Niech
jest ustaloną liczbą naturalną, większą od 4, losujemy jednocześnie trzy liczby. Niech 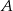 oznacza zdarzenie: suma wylosowanych liczb nie ulegnie zmianie, jeżeli w wylosowanych liczbach zmienimy znaki na przeciwne. Wiedząc, że
oznacza zdarzenie: suma wylosowanych liczb nie ulegnie zmianie, jeżeli w wylosowanych liczbach zmienimy znaki na przeciwne. Wiedząc, że 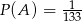 , oblicz
, oblicz  .
.
W grze liczbowej Express Lotek losowanych jest pięć spośród liczb 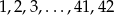 . Gracz zawarł jeden zakład na najbliższe losowanie (czyli wytypował w kolekturze Totalizatora Sportowego pięć liczb spośród czterdziestu dwóch). Oblicz ile razy prawdopodobieństwo trafienia ’trójki’ (czyli wytypowania dokładnie 3 liczb spośród tych, które będą wylosowane) jest większe niż prawdopodobieństwo trafienia
. Gracz zawarł jeden zakład na najbliższe losowanie (czyli wytypował w kolekturze Totalizatora Sportowego pięć liczb spośród czterdziestu dwóch). Oblicz ile razy prawdopodobieństwo trafienia ’trójki’ (czyli wytypowania dokładnie 3 liczb spośród tych, które będą wylosowane) jest większe niż prawdopodobieństwo trafienia
- piątki;
- czwórki.
Spośród liczb naturalnych trzycyfrowych wybieramy jedną liczbę. Jakie jest prawdopodobieństwo wybrania liczby, która przy dzieleniu przez 11 daje resztę 3.
Spośród liczb naturalnych trzycyfrowych wybieramy jedną liczbę. Jakie jest prawdopodobieństwo wybrania liczby, która przy dzieleniu przez 11 daje resztę 5.
Dane są dwa podzbiory zbioru liczb całkowitych:
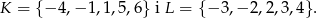
Z każdego z nich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest dodatni.
Ze zbioru pięciu liczb 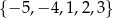 losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie
losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie 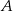 polega na wylosowaniu dwóch liczb, których iloczyn jest ujemny. Oblicz prawdopodobieństwo zdarzenia
polega na wylosowaniu dwóch liczb, których iloczyn jest ujemny. Oblicz prawdopodobieństwo zdarzenia 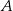 .
.
Dane są dwa podzbiory zbioru liczb całkowitych:
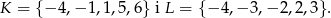
Z każdego z nich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest dodatni.
Dane są dwa podzbiory zbioru liczb całkowitych:
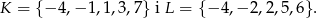
Z każdego z nich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest ujemny.
Z liczb ośmioelementowego zbioru 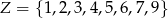 tworzymy ośmiowyrazowy ciąg, którego wyrazy się nie powtarzają. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że żadne dwie liczby parzyste nie są sąsiednimi wyrazami utworzonego ciągu. Wynik przedstaw w postaci ułamka zwykłego nieskracalnego.
tworzymy ośmiowyrazowy ciąg, którego wyrazy się nie powtarzają. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że żadne dwie liczby parzyste nie są sąsiednimi wyrazami utworzonego ciągu. Wynik przedstaw w postaci ułamka zwykłego nieskracalnego.
Ze zbioru 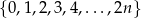 gdzie
gdzie 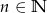 wylosowano jednocześnie 3 liczby. Prawdopodobieństwo, że suma wylosowanych liczb jest nieparzysta wynosi
wylosowano jednocześnie 3 liczby. Prawdopodobieństwo, że suma wylosowanych liczb jest nieparzysta wynosi 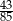 . Wyznacz ile liczb było w zbiorze.
. Wyznacz ile liczb było w zbiorze.
Ze zbioru 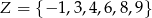 losujemy bez zwracania liczby
losujemy bez zwracania liczby  i
i 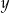 . Oblicz prawdopodobieństwa zdarzeń:
. Oblicz prawdopodobieństwa zdarzeń: 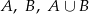 jeśli:
jeśli:
A – suma wylosowanych liczb jest nieparzysta;
B – wylosowane liczby spełniają warunek: 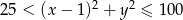 .
.
Ze zbioru wszystkich liczb naturalnych czterocyfrowych, których cyfra tysięcy i cyfra setek należą do zbioru 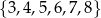 , a cyfra dziesiątek i cyfra jedności należą do zbioru
, a cyfra dziesiątek i cyfra jedności należą do zbioru 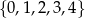 , losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę czterocyfrową, która jest podzielna przez 4.
, losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę czterocyfrową, która jest podzielna przez 4.
Ze zbioru liczb dwucyfrowych losujemy jedną liczbę. Jakie jest prawdopodobieństwo, że iloczyn cyfr wylosowanej liczby jest dodatnią liczbą złożoną?
Ze zbioru liczb 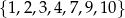 losujemy dwie liczby (mogą się powtarzać). Oblicz prawdopodobieństwo, że suma wylosowanych liczb jest parzysta.
losujemy dwie liczby (mogą się powtarzać). Oblicz prawdopodobieństwo, że suma wylosowanych liczb jest parzysta.
Ze zbioru 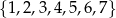 losujemy liczbę
losujemy liczbę  , a ze zbioru
, a ze zbioru 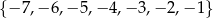 liczbę
liczbę 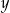 . Oblicz prawdopodobieństwo tego, że
. Oblicz prawdopodobieństwo tego, że 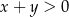 .
.
Ze zbioru liczb 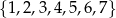 losujemy kolejno dwa razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia
losujemy kolejno dwa razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia 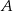 polegającego na tym, że pierwsza z wylosowanych liczb jest nieparzysta, a ich iloczyn jest większy od 10.
polegającego na tym, że pierwsza z wylosowanych liczb jest nieparzysta, a ich iloczyn jest większy od 10.
Ze zbioru 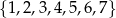 losujemy liczbę
losujemy liczbę  , a ze zbioru
, a ze zbioru 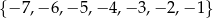 liczbę
liczbę 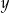 . Oblicz prawdopodobieństwo tego, że
. Oblicz prawdopodobieństwo tego, że 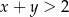 .
.
Ze zbioru 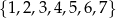 losujemy liczbę
losujemy liczbę  , a ze zbioru
, a ze zbioru 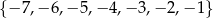 liczbę
liczbę 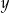 . Oblicz prawdopodobieństwo tego, że
. Oblicz prawdopodobieństwo tego, że 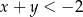 .
.
Ze zbioru liczb 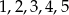 losujemy kolejno trzy razy po jednej liczbie bez zwracania tworząc liczbę trzycyfrową. Oblicz prawdopodobieństwo zdarzenia
losujemy kolejno trzy razy po jednej liczbie bez zwracania tworząc liczbę trzycyfrową. Oblicz prawdopodobieństwo zdarzenia 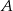 – otrzymana liczba jest mniejsza od 432.
– otrzymana liczba jest mniejsza od 432.
Ze zbioru liczb 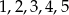 losujemy kolejno trzy razy po jednej liczbie bez zwracania tworząc liczbę trzycyfrową. Oblicz prawdopodobieństwo zdarzenia
losujemy kolejno trzy razy po jednej liczbie bez zwracania tworząc liczbę trzycyfrową. Oblicz prawdopodobieństwo zdarzenia 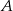 – otrzymana liczba jest większa od 324.
– otrzymana liczba jest większa od 324.
Ze zbioru 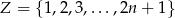 , gdzie
, gdzie 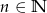 wylosowano równocześnie dwie liczby. Wyznacz
wylosowano równocześnie dwie liczby. Wyznacz  , tak aby prawdopodobieństwo wylosowania liczb, których suma jest liczbą nieparzystą było większe od
, tak aby prawdopodobieństwo wylosowania liczb, których suma jest liczbą nieparzystą było większe od 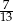 .
.
Ze zbioru 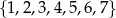 losujemy kolejno, bez zwracania trzy cyfry i tworzymy liczbę trzycyfrową: pierwsza wylosowana cyfra jest cyfrą setek, druga – cyfrą dziesiątek, a trzecia – cyfrą jedności. Oblicz prawdopodobieństwo zdarzenia, że otrzymana liczba ma następującą własność: różnica między największą i najmniejszą cyfrą tej liczby jest nie większa niż 3.
losujemy kolejno, bez zwracania trzy cyfry i tworzymy liczbę trzycyfrową: pierwsza wylosowana cyfra jest cyfrą setek, druga – cyfrą dziesiątek, a trzecia – cyfrą jedności. Oblicz prawdopodobieństwo zdarzenia, że otrzymana liczba ma następującą własność: różnica między największą i najmniejszą cyfrą tej liczby jest nie większa niż 3.
Losujemy jedną liczbę całkowitą z przedziału 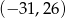 i jedną liczbę całkowitą z przedziału
i jedną liczbę całkowitą z przedziału 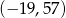 . Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest dodatni. Wynik podaj w postaci ułamka nieskracalnego.
. Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest dodatni. Wynik podaj w postaci ułamka nieskracalnego.
Losujemy jedną liczbę całkowitą z przedziału 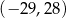 i jedną liczbę całkowitą z przedziału
i jedną liczbę całkowitą z przedziału 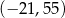 . Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest ujemny. Wynik podaj w postaci ułamka nieskracalnego.
. Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest ujemny. Wynik podaj w postaci ułamka nieskracalnego.
Spośród liczb 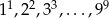 wybieramy losowo trzy. Oblicz prawdopodobieństwo, że iloczyn tych liczb jest parzysty.
wybieramy losowo trzy. Oblicz prawdopodobieństwo, że iloczyn tych liczb jest parzysty.
Ze zbioru 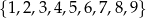 losujemy kolejno ze zwracaniem trzy liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie spośród trzech wylosowanych liczb będą równe. Wynik zapisz w postaci ułamka nieskracalnego.
losujemy kolejno ze zwracaniem trzy liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie spośród trzech wylosowanych liczb będą równe. Wynik zapisz w postaci ułamka nieskracalnego.
Z cyfr 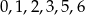 tworzymy liczbę czterocyfrową, przy czym cyfry nie mogą się powtarzać. Jakie jest prawdopodobieństwo otrzymania liczby podzielnej przez 25?
tworzymy liczbę czterocyfrową, przy czym cyfry nie mogą się powtarzać. Jakie jest prawdopodobieństwo otrzymania liczby podzielnej przez 25?

