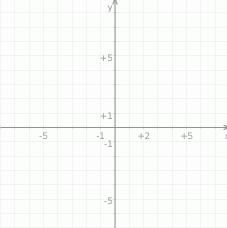
Dla każdej liczby rzeczywistej 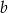 równanie
równanie 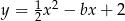 opisuje pewną parabolę. Wyznacz wszystkie wartości parametru
opisuje pewną parabolę. Wyznacz wszystkie wartości parametru 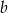 , dla których wierzchołek paraboli leży nad osią
, dla których wierzchołek paraboli leży nad osią 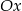 .
.
/Szkoła średnia/Funkcje - wykresy
Napisz równanie stycznej do krzywej 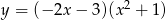 w punkcie
w punkcie 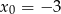 .
.
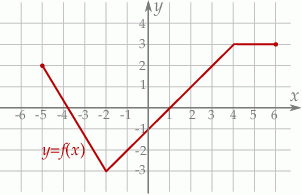
Dany jest wykres funkcji 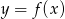 określonej dla
określonej dla 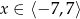 .
.
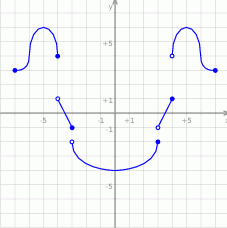
Odczytaj z wykresu:
- rozwiązania równania
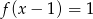 ;
; - miejsca zerowe funkcji
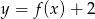 ;
; - maksymalne przedziały monotoniczności funkcji
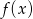 .
.
Dany jest wykres funkcji 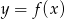 określonej dla
określonej dla 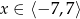 .
.
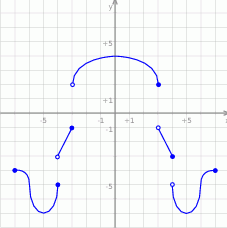
Odczytaj z wykresu:
- rozwiązania równania
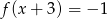 ;
; - miejsca zerowe funkcji
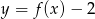 ;
; - maksymalne przedziały monotoniczności funkcji
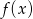 .
.
Napisz równanie stycznej do krzywej 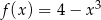 wiedząc, że jest ona równoległa do prostej
wiedząc, że jest ona równoległa do prostej 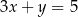 .
.
Funkcja 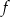 określona jest wzorem
określona jest wzorem 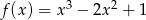 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania tych stycznych do wykresu funkcji
. Wyznacz równania tych stycznych do wykresu funkcji 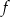 , które są równoległe do prostej o równaniu
, które są równoległe do prostej o równaniu 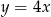 .
.
Funkcja 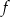 określona jest wzorem
określona jest wzorem 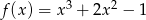 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania tych stycznych do wykresu funkcji
. Wyznacz równania tych stycznych do wykresu funkcji 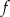 , które są równoległe do prostej o równaniu
, które są równoległe do prostej o równaniu 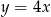 .
.
Wykres funkcji 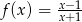 przekształcono w symetrii względem prostej
przekształcono w symetrii względem prostej 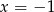 i otrzymano wykres funkcji
i otrzymano wykres funkcji 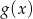 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 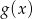 .
.
Na rysunku przedstawiono wykres funkcji 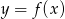 .
.
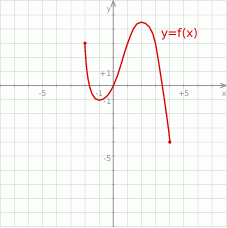
Naszkicuj wykres funkcji: 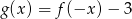 . Określ dziedzinę oraz miejsca zerowe funkcji
. Określ dziedzinę oraz miejsca zerowe funkcji 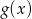 .
.
- Zaznacz w układzie współrzędnych zbiór
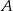 punktów, których współrzędne
punktów, których współrzędne 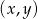 spełniają warunek:
spełniają warunek: 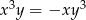 .
. - Wiedząc, że wykres funkcji homograficznej
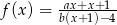 nie ma punktów wspólnych ze zbiorem
nie ma punktów wspólnych ze zbiorem 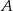 wyznacz
wyznacz  i
i 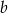 .
.
Funkcja 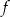 jest określona wzorem
jest określona wzorem 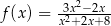 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Punkt
. Punkt 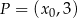 należy do wykresu funkcji
należy do wykresu funkcji 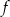 . Oblicz
. Oblicz 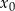 oraz wyznacz równanie stycznej do wykresu funkcji
oraz wyznacz równanie stycznej do wykresu funkcji 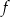 w punkcie
w punkcie 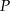 .
.
Wykres funkcji kwadratowej 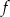 danej wzorem
danej wzorem 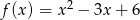 przecięto prostymi o równaniach
przecięto prostymi o równaniach 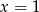 oraz
oraz 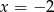 . Oblicz odległość między punktami przecięcia tych prostych z wykresem funkcji
. Oblicz odległość między punktami przecięcia tych prostych z wykresem funkcji 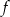 .
.
Wykres funkcji kwadratowej 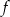 danej wzorem
danej wzorem 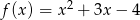 przecięto prostymi o równaniach
przecięto prostymi o równaniach 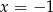 oraz
oraz 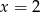 . Oblicz odległość między punktami przecięcia tych prostych z wykresem funkcji
. Oblicz odległość między punktami przecięcia tych prostych z wykresem funkcji 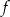 .
.
Na rysunku przedstawiony jest wykres funkcji 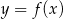 .
.
- Sporządź (na tym samym rysunku) wykres funkcji
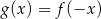 .
. - Podaj maksymalny przedział, w którym funkcja
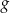 jest rosnąca.
jest rosnąca.
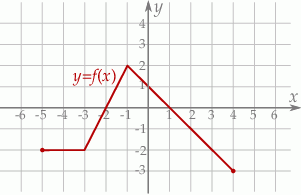
Na rysunku przedstawiony jest wykres funkcji 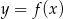 .
.
- Sporządź (na tym samym rysunku) wykres funkcji
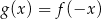 .
. - Podaj maksymalny przedział, w którym funkcja
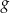 jest rosnąca.
jest rosnąca.
Wykres funkcji  przekształcono w symetrii względem prostej
przekształcono w symetrii względem prostej 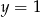 i otrzymano wykres funkcji
i otrzymano wykres funkcji 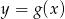 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 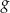 .
.
Dziedziną funkcji 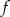 opisanej wzorem
opisanej wzorem 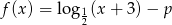 jest przedział
jest przedział 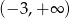 . Wiedząc, że do wykresu funkcji
. Wiedząc, że do wykresu funkcji 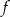 należy punkt
należy punkt 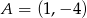 , oblicz wartość parametru
, oblicz wartość parametru 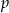 . Następnie:
. Następnie:
- naszkicuj wykres funkcji
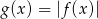 ;
; - wyznacz zbiór wszystkich wartości parametru
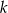 , dla których równanie
, dla których równanie 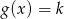 ma dwa rozwiązania różnych znaków.
ma dwa rozwiązania różnych znaków.
Wyznacz wszystkie funkcje kwadratowe, których wykres przechodzi przez punkty 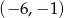 oraz
oraz 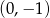 .
.
Punkty 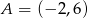 i
i 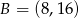 należą do wykresu funkcji
należą do wykresu funkcji 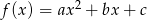 . Funkcja
. Funkcja 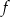 ma dwa miejsca zerowe, a wierzchołek paraboli będącej jej wykresem należy do prostej
ma dwa miejsca zerowe, a wierzchołek paraboli będącej jej wykresem należy do prostej 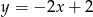 . Znajdź wzór tej funkcji.
. Znajdź wzór tej funkcji.
Na podstawie wykresu funkcji kwadratowej podaj jej wzór.
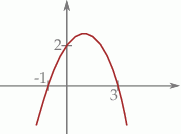
Na podstawie przedstawionego fragmentu wykresu funkcji kwadratowej wyznacz jej wzór.
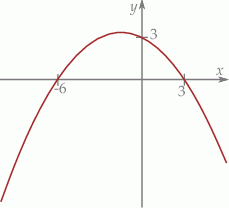
Wyznacz wszystkie wartości parametru  , dla których prosta o równaniu
, dla których prosta o równaniu 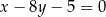 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 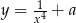 .
.
Pole obszaru ograniczonego wykresem funkcji 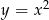 dla
dla 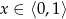 i osią
i osią 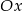 możemy obliczyć z dowolną dokładnością, zwiększając liczbę
możemy obliczyć z dowolną dokładnością, zwiększając liczbę  prostokątów o szerokości
prostokątów o szerokości 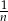 każdy (patrz rysunek) i sumując ich pola.
każdy (patrz rysunek) i sumując ich pola.
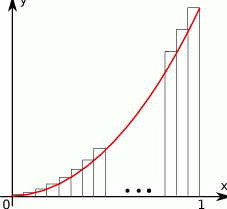
- Przedstaw ilustrację graficzną takiej sytuacji dla
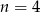 i oblicz sumę pól otrzymanych prostokątów.
i oblicz sumę pól otrzymanych prostokątów. 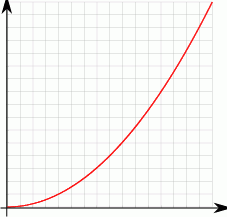
- Oblicz sumę
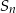 pól
pól  prostokątów, wykorzystując wzór:
prostokątów, wykorzystując wzór: 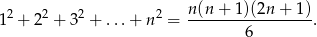
Podaj dla jakich wartości parametru 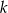 punkt przecięcia się wykresów funkcji
punkt przecięcia się wykresów funkcji 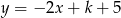 i
i 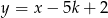 należy do II ćwiartki układu współrzędnych.
należy do II ćwiartki układu współrzędnych.
Podaj dla jakich wartości parametru 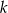 punkt przecięcia się wykresów funkcji
punkt przecięcia się wykresów funkcji 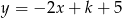 i
i 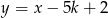 należy do półpłaszczyzny opisanej nierównością
należy do półpłaszczyzny opisanej nierównością 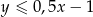 .
.
Na rysunku przedstawiono fragment wykresu funkcji 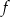 , który powstał w wyniku przesunięcia wykresu funkcji określonej wzorem
, który powstał w wyniku przesunięcia wykresu funkcji określonej wzorem 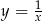 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 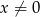 .
.
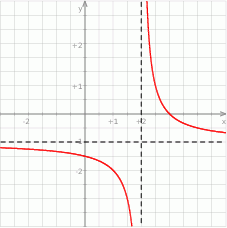
- Odczytaj z wykresu i zapisz zbiór tych wszystkich argumentów, dla których wartości funkcji
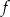 są większe od 0.
są większe od 0. - Podaj miejsce zerowe funkcji
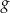 określonej wzorem
określonej wzorem 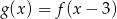 .
.
Naszkicuj wykres funkcji
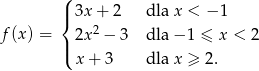
Odczytaj z wykresu maksymalne przedziały monotoniczności funkcji 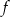 .
.