Z talii 52 kart wylosowano jedną kartę. Jakie jest prawdopodobieństwo, że wylosowano damę jeżeli wiadomo, że wylosowana karta nie jest ani kierem ani królem?
A) 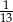 B)
B) 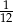 C)
C) 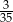 D)
D) 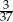
/Szkoła średnia/Zadania testowe/Prawdopodobieństwo
Z urny zawierającej kule w dwóch kolorach wybieramy losowo dwie. Prawdopodobieństwo wylosowania co najmniej jednej kuli białej jest równe 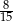 , a prawdopodobieństwo wybrania co najwyżej jednej kuli białej jest równe
, a prawdopodobieństwo wybrania co najwyżej jednej kuli białej jest równe 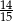 . Wobec tego prawdopodobieństwo wybrania dokładnie jednej kuli białej jest równe
. Wobec tego prawdopodobieństwo wybrania dokładnie jednej kuli białej jest równe
A) 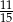 B)
B) 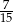 C)
C) 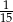 D)
D) 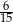
Z szuflady zawierającej piłki w dwóch kolorach wybieramy losowo dwie. Prawdopodobieństwo wylosowania co najmniej jednej piłki czerwonej jest równe 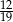 , a prawdopodobieństwo wybrania co najmniej jednej piłki zielonej jest równe
, a prawdopodobieństwo wybrania co najmniej jednej piłki zielonej jest równe 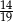 . Wobec tego prawdopodobieństwo wybrania dokładnie jednej piłki czerwonej jest równe
. Wobec tego prawdopodobieństwo wybrania dokładnie jednej piłki czerwonej jest równe
A) 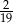 B)
B) 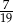 C)
C) 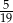 D)
D) 
Ze zbioru kolejnych liczb naturalnych 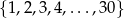 losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest kwadratem liczby całkowitej, jest równe
losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest kwadratem liczby całkowitej, jest równe
A) 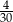 B)
B) 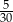 C)
C) 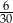 D)
D) 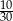
Ze zbioru kolejnych liczb naturalnych 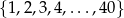 losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest kwadratem liczby całkowitej, jest równe
losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest kwadratem liczby całkowitej, jest równe
A) 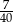 B)
B) 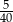 C)
C) 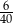 D)
D) 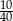
Ze zbioru kolejnych liczb naturalnych 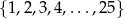 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby, która jest kwadratem liczby całkowitej, jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby, która jest kwadratem liczby całkowitej, jest równe
A) 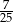 B)
B) 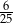 C)
C) 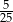 D)
D) 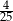
Dane są dwie urny z kulami, w każdej jest 5 kul. W pierwszej urnie jest jedna kula biała i 4 kule czarne. W drugiej urnie są 3 kule białe i 2 kule czarne. Rzucamy jeden raz symetryczną sześcienną kostką do gry. Jeśli wypadnie jedno lub dwa oczka, to losujemy jedną kulę z pierwszej urny, natomiast jeśli wypadną co najmniej trzy oczka, to losujemy jedną kulę z drugiej urny. Prawdopodobieństwo wylosowania kuli białej jest równe
A) 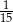 B)
B) 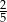 C)
C) 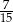 D)
D) 
Dane są dwie urny z kulami. W każdej z urn jest siedem kul. W pierwszej urnie są jedna kula biała i sześć kul czarnych, w drugiej urnie są cztery kule białe i trzy kule czarne. Rzucamy jeden raz symetryczną monetą. Jeżeli wypadnie reszka, to losujemy jedną kulę z pierwszej urny, w przeciwnym przypadku – jedną kulę z drugiej urny. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy kulę białą w tym doświadczeniu, jest równe
A) 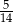 B)
B) 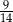 C)
C)  D)
D) 
Dane są dwie urny z kulami, w każdej jest 5 kul. W pierwszej urnie jest jedna kula biała i 4 kule czarne. W drugiej urnie są 3 kule białe i 2 kule czarne. Rzucamy jeden raz symetryczną sześcienną kostką do gry. Jeśli wypadnie jedno lub dwa oczka, to losujemy jedną kulę z pierwszej urny, natomiast jeśli wypadną co najmniej trzy oczka, to losujemy jedną kulę z drugiej urny. Prawdopodobieństwo wylosowania kuli czarnej jest równe
A) 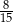 B)
B) 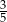 C)
C) 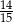 D)
D) 
Dane są dwie urny z kulami, w każdej jest 5 kul. W pierwszej urnie są dwie kule białe i 3 kule czarne. W drugiej urnie są 3 kule białe i 2 kule czarne. Rzucamy jeden raz symetryczną sześcienną kostką do gry. Jeśli wypadnie jedno lub dwa oczka, to losujemy jedną kulę z pierwszej urny, natomiast jeśli wypadną co najmniej trzy oczka, to losujemy jedną kulę z drugiej urny. Prawdopodobieństwo wylosowania kuli białej jest równe
A) 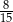 B)
B) 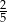 C)
C) 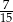 D)
D) 
Dane są dwie urny z kulami, w każdej jest 5 kul. W pierwszej urnie są dwie kule białe i 3 kule czarne. W drugiej urnie są 3 kule białe i 2 kule czarne. Rzucamy jeden raz symetryczną sześcienną kostką do gry. Jeśli wypadnie jedno lub dwa oczka, to losujemy jedną kulę z pierwszej urny, natomiast jeśli wypadną co najmniej trzy oczka, to losujemy jedną kulę z drugiej urny. Prawdopodobieństwo wylosowania kuli czarnej jest równe
A) 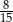 B)
B) 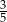 C)
C) 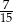 D)
D) 
Na loterii jest 10 losów, z których 4 są wygrywające. Kupujemy jeden los. Prawdopodobieństwo zdarzenia, że nie wygramy nagrody, jest równe
A)  B)
B)  C)
C)  D)
D) 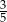
W pudełku jest 50 kuponów, wśród których jest 15 kuponów przegrywających, a pozostałe kupony są wygrywające. Z tego pudełka w sposób losowy wyciągamy jeden kupon. Prawdopodobieństwo zdarzenia polegającego na tym, że wyciągniemy kupon wygrywający, jest równe
A) 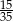 B)
B) 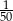 C)
C) 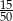 D)
D) 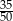
Na loterii jest 12 losów, z których 8 jest przegrywających. Kupujemy jeden los. Prawdopodobieństwo zdarzenia, że wygramy nagrodę jest równe
A) 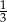 B)
B) 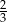 C)
C) 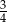 D)
D) 
Na loterii jest 20 losów, z których 8 jest wygrywających. Kupujemy jeden los. Prawdopodobieństwo zdarzenia, że nie wygramy nagrody jest równe
A) 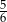 B)
B) 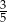 C)
C) 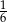 D)
D) 
Na loterii jest 14 losów, z których 6 jest wygrywających. Kupujemy jeden los. Prawdopodobieństwo zdarzenia, że nie wygramy nagrody jest równe
A)  B)
B)  C)
C) 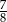 D)
D) 
W pewnej klasie stosunek liczby dziewcząt do liczby chłopców jest równy 4:5. Losujemy jedną osobę z tej klasy. Prawdopodobieństwo tego, że będzie to dziewczyna, jest równe
A) 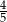 B)
B)  C)
C) 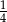 D)
D) 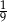
Pewne przedsiębiorstwo postanowiło przyznać każdemu pracownikowi losowy 5-cyfrowy identyfikator, przy czym ustalono, że w identyfikatorze nie może występować cyfra 0. Prawdopodobieństwo 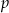 otrzymania identyfikatora, w którym każde dwie cyfry są różne spełnia warunek
otrzymania identyfikatora, w którym każde dwie cyfry są różne spełnia warunek
A) 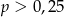 B)
B) 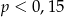 C)
C) 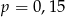 D)
D) 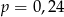
Rzucamy trzy razy symetryczną monetą. Niech 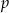 oznacza prawdopodobieństwo otrzymania dokładnie dwóch orłów w tych trzech rzutach. Wtedy
oznacza prawdopodobieństwo otrzymania dokładnie dwóch orłów w tych trzech rzutach. Wtedy
A) 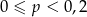 B)
B) 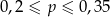 C)
C) 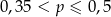 D)
D) 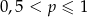
Rzucamy trzy razy symetryczną monetą. Niech 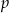 oznacza prawdopodobieństwo otrzymania co najwyżej jednej reszki w tych trzech rzutach. Wtedy
oznacza prawdopodobieństwo otrzymania co najwyżej jednej reszki w tych trzech rzutach. Wtedy
A) 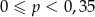 B)
B) 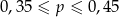 C)
C) 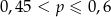 D)
D) 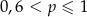
Rzucamy trzy razy symetryczną monetą. Niech 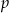 oznacza prawdopodobieństwo otrzymania dokładnie jednego orła w tych trzech rzutach. Wtedy
oznacza prawdopodobieństwo otrzymania dokładnie jednego orła w tych trzech rzutach. Wtedy
A) 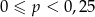 B)
B) 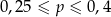 C)
C) 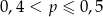 D)
D) 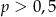
Ze zbioru 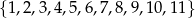 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
A) 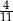 B)
B) 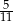 C)
C) 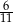 D)
D) 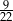
Ze zbioru liczb 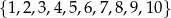 losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczby pierwszej jest równe
losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczby pierwszej jest równe
A) 0,5 B) 0,6 C) 0,4 D) 0,8
Ze zbioru 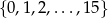 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
A) 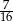 B)
B)  C)
C) 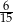 D)
D) 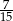
Ze zbioru 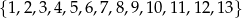 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
A) 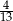 B)
B) 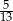 C)
C) 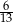 D)
D) 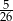
Prawdopodobieństwo zdarzenia 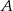 jest równe
jest równe 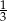 , a prawdopodobieństwo sumy zdarzeń
, a prawdopodobieństwo sumy zdarzeń 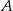 i
i 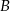 jest równe
jest równe 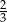 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 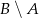 jest równe
jest równe
A) 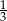 B)
B)  C)
C) 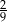 D)
D) 
Prawdopodobieństwo zdarzenia 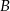 jest równe
jest równe 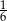 , a prawdopodobieństwo sumy zdarzeń
, a prawdopodobieństwo sumy zdarzeń 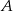 i
i 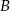 jest równe
jest równe 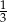 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 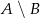 jest równe
jest równe
A) 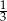 B)
B)  C)
C)  D)
D) 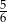
Jeżeli 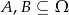 oraz
oraz 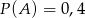 i
i 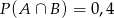 to prawdopodobieństwo
to prawdopodobieństwo 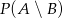 jest równe
jest równe
A) 0,6 B) 0,4 C) 1 D) 0
W każdym z czterech pojemników znajduje się para kul, z których jedna jest czerwona, a druga – niebieska. Z każdego pojemnika losujemy jedną kulę. Niech 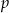 oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie z czterech wylosowanych kul będą niebieskie. Wtedy
oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie z czterech wylosowanych kul będą niebieskie. Wtedy
A) 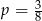 B)
B) 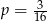 C)
C) 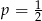 D)
D) 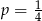
W pudełku znajdują się dwie kule: czarna i biała. Czterokrotnie losujemy ze zwracaniem jedną kulę z tego pudełka. Prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwa razy w czterech losowaniach wyciągniemy kulę koloru czarnego, jest równe
A) 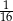 B)
B)  C)
C) 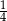 D)
D) 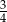
W każdym z pięciu pojemników znajduje się para kul, z których jedna jest czerwona, a druga – niebieska. Z każdego pojemnika losujemy jedną kulę. Niech 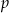 oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie z pięciu wylosowanych kul będą niebieskie. Wtedy
oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie z pięciu wylosowanych kul będą niebieskie. Wtedy
A) 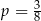 B)
B) 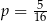 C)
C) 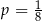 D)
D) 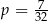
W pudełku znajdują się dwie kule: czarna i biała. Czterokrotnie losujemy ze zwracaniem jedną kulę z tego pudełka. Prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie trzy razy w czterech losowaniach wyciągniemy kulę koloru białego, jest równe
A) 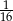 B)
B)  C)
C) 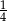 D)
D) 
Dane są dwie urny z kulami. W pierwszej urnie jest 10 kul: 8 białych i 2 czarne, w drugiej jest 8 kul: 5 białych i 3 czarne. Wylosowanie każdej z urn jest jednakowo prawdopodobne. Wylosowano jedną z tych urn i wyciągnięto z niej losowo jedną kulę. Wyciągnięta kula była czarna. Prawdopodobieństwo zdarzenia, że wylosowana kula pochodziła z pierwszej z tych urn, jest równe
A) 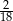 B)
B) 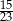 C)
C) 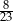 D)
D) 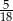
Dane są dwie urny z kulami. W pierwszej urnie jest 10 kul: 8 białych i 2 czarne, w drugiej jest 8 kul: 5 białych i 3 czarne. Wylosowanie każdej z urn jest jednakowo prawdopodobne. Wylosowano jedną z tych urn i wyciągnięto z niej losowo jedną kulę. Wyciągnięta kula była biała. Prawdopodobieństwo zdarzenia, że wylosowana kula pochodziła z drugiej z tych urn, jest równe
A) 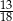 B)
B) 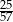 C)
C) 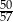 D)
D) 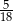
Mamy dwie urny. W pierwszej są 3 kule białe i 7 kul czarnych, w drugiej jest jedna kula biała i 9 kul czarnych. Rzucamy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek, od jednego oczka do sześciu oczek. Jeśli w wyniku rzutu otrzymamy ściankę z jednym oczkiem, to losujemy jedną kulę z pierwszej urny, w przeciwnym przypadku – losujemy jedną kulę z drugiej urny. Wtedy prawdopodobieństwo wylosowania kuli białej jest równe
A) 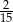 B)
B) 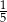 C)
C) 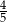 D)
D) 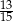
Mamy dwie urny. W pierwszej jest 5 kul białych i 5 kul czarnych, w drugiej są 3 kule białe i 7 kul czarnych. Rzucamy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek, od jednego oczka do sześciu oczek. Jeśli w wyniku rzutu otrzymamy ściankę z liczbą oczek podzielną przez 3, to losujemy jedną kulę z pierwszej urny, w przeciwnym przypadku – losujemy jedną kulę z drugiej urny. Wtedy prawdopodobieństwo wylosowania kuli białej jest równe
A) 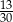 B)
B) 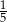 C)
C) 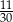 D)
D) 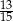
Niepuste zdarzenia losowe 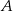 i
i 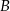 zawarte w
zawarte w 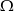 są takie, że
są takie, że 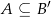 , gdzie
, gdzie 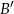 oznacza zdarzenie przeciwne do zdarzenia
oznacza zdarzenie przeciwne do zdarzenia 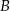 . Wynika stąd, że
. Wynika stąd, że
A) 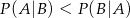 B)
B) 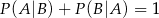
C) 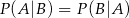 D)
D) 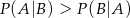
W pudełku znajdują się płytki z literami i cyframi. Na każdej płytce jest wydrukowana albo jedna wielka litera, albo jedna mała litera, albo jedna cyfra. Płytek z wielkimi literami jest o 25% mniej niż płytek z cyframi, a płytek z małymi literami jest o 40% więcej niż płytek z wielkimi literami. Losujemy jedną płytkę. Prawdopodobieństwo wylosowania płytki z cyfrą jest równe
A) 0,85 B) 0,1 C) 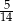 D)
D) 
Ze zbioru dwucyfrowych liczb naturalnych wybieramy losowo jedną liczbę. Prawdopodobieństwo otrzymania liczby podzielnej przez 30 jest równe
A) 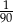 B)
B) 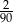 C)
C) 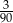 D)
D) 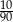
Ze zbioru dwucyfrowych liczb naturalnych wybieramy losowo jedną liczbę. Prawdopodobieństwo otrzymania liczby podzielnej przez 15 jest równe
A) 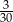 B)
B) 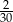 C)
C) 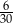 D)
D) 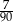
Ze zbioru liczb naturalnych dwucyfrowych nie mniejszych od 50 losujemy jedną liczbę. Jakie jest prawdopodobieństwo, że wylosowana liczba będzie podzielna przez 5?
A) 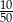 B)
B) 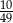 C)
C) 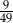 D)
D) 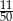
Ze zbioru liczb naturalnych dwucyfrowych nie mniejszych od 40 losujemy jedną liczbę. Jakie jest prawdopodobieństwo, że wylosowana liczba będzie podzielna przez 5?
A) 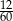 B)
B) 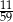 C)
C) 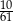 D)
D) 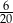
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo dwukrotnego otrzymania liczby oczek różnej od 5 jest równe
A)  B)
B) 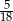 C)
C) 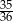 D)
D) 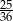
Ściany sześciennej kostki ponumerowano liczbami od 1 do 6. Następnie w sposób losowy wybrano jedną z krawędzi tego sześcianu. Prawdopodobieństwo zdarzenia polegające na tym, że wylosowana krawędź jest krawędzią ściany z numerem 6 jest równe
A) 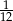 B)
B) 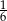 C)
C) 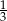 D)
D) 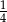
Ze zbioru dzielników naturalnych liczby 8 losujemy dwa razy po jednej liczbie (otrzymane liczby mogą się powtarzać). Prawdopodobieństwo, że iloczyn wybranych liczb jest dzielnikiem liczby 4 jest równe
A) 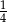 B)
B) 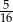 C)
C) 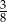 D)
D) 
Ze zbioru dzielników naturalnych liczby 12 losujemy dwa razy po jednej liczbie (otrzymane liczby mogą się powtarzać). Prawdopodobieństwo, że iloczyn wybranych liczb jest dzielnikiem liczby 6 jest równe
A) 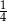 B)
B) 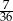 C)
C) 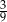 D)
D) 
Zdarzenia losowe 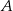 i
i 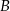 zawarte w
zawarte w 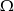 są takie, że prawdopodobieństwo
są takie, że prawdopodobieństwo 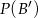 zdarzenia
zdarzenia 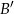 , przeciwnego do zdarzenia
, przeciwnego do zdarzenia 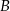 , jest równe
, jest równe 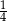 . Ponadto prawdopodobieństwo warunkowe
. Ponadto prawdopodobieństwo warunkowe 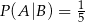 . Wynika stąd, że
. Wynika stąd, że
A) 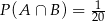 B)
B) 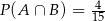 C)
C) 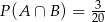 D)
D) 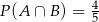
Zdarzenia losowe 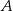 i
i 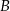 zawarte w
zawarte w 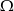 są takie, że prawdopodobieństwo
są takie, że prawdopodobieństwo 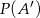 zdarzenia
zdarzenia 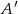 , przeciwnego do zdarzenia
, przeciwnego do zdarzenia 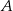 , jest równe
, jest równe  . Ponadto, prawdopodobieństwo warunkowe
. Ponadto, prawdopodobieństwo warunkowe 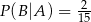 . Wynika stąd, że
. Wynika stąd, że
A) 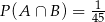 B)
B) 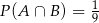 C)
C) 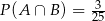 D)
D)