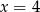Wiedząc, że dla sum częściowych pewnego ciągu geometrycznego o wyrazach dodatnich prawdziwa jest równość 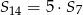 , oblicz iloraz tego ciągu.
, oblicz iloraz tego ciągu.
/Szkoła średnia
Niech 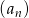 oznacza ciąg geometryczny o wyrazach dodatnich, natomiast
oznacza ciąg geometryczny o wyrazach dodatnich, natomiast 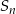 niech oznacza sumę
niech oznacza sumę  początkowych wyrazów tego ciągu. Wiedząc, że
początkowych wyrazów tego ciągu. Wiedząc, że 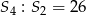 , oblicz
, oblicz 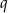 .
.
Udowodnij, że średnica okręgu wpisanego w trapez równoramienny, ma długość równą średniej geometrycznej długości podstaw trapezu.
Trapez równoramienny 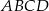 o podstawach
o podstawach 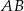 i
i 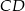 jest opisany na okręgu o promieniu
jest opisany na okręgu o promieniu  . Wykaż, że
. Wykaż, że 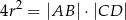 .
.
Punkty 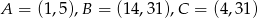 są wierzchołkami trójkąta. Prosta zawierająca wysokość tego trójkąta poprowadzona z wierzchołka
są wierzchołkami trójkąta. Prosta zawierająca wysokość tego trójkąta poprowadzona z wierzchołka 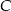 przecina prostą
przecina prostą 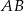 w punkcie
w punkcie 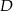 . Oblicz długość odcinka
. Oblicz długość odcinka 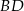 .
.
Punkty 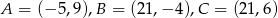 są wierzchołkami trójkąta. Prosta zawierająca wysokość tego trójkąta poprowadzona z wierzchołka
są wierzchołkami trójkąta. Prosta zawierająca wysokość tego trójkąta poprowadzona z wierzchołka 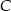 przecina prostą
przecina prostą 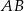 w punkcie
w punkcie 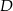 . Oblicz długość odcinka
. Oblicz długość odcinka 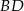 .
.
Połączono ramiona trapezu odcinkiem równoległym do podstaw i dzielącym te ramiona w stosunku 2:3 licząc od krótszej podstawy. Oblicz długość tego odcinka, jeśli wiesz, że podstawy trapezu mają długości  i
i 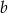 , gdzie
, gdzie 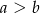 .
.
Ile jest wszystkich czterocyfrowych liczb naturalnych mniejszych niż 2017?
A) 2016 B) 2017 C) 1016 D) 1017
Ile jest wszystkich czterocyfrowych liczb naturalnych większych niż 2018?
A) 7979 B) 7980 C) 7981 D) 7982
W konkursie matematycznym, w którym przewidziano tylko jedną nagrodę I stopnia, bierze udział 15 uczniów. Prawdopodobieństwo, że zwycięży Agnieszka jest równe 0,20. Prawdopodobieństwo, że zwycięży Piotrek jest równe 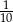 . Prawdopodobieństwo, że zwycięży Agnieszka lub Piotrek jest równe
. Prawdopodobieństwo, że zwycięży Agnieszka lub Piotrek jest równe
A) 0,02 B) 0,3 C) 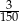 D)
D) 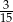
W zawodach pływackich, w których przewidziano tylko jedną nagrodę I stopnia, bierze udział 35 uczniów. Prawdopodobieństwo, że zwycięży Jola jest równe 0,10. Prawdopodobieństwo, że zwycięży Antek jest równe 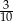 . Prawdopodobieństwo, że zwycięży Jola lub Antek jest równe
. Prawdopodobieństwo, że zwycięży Jola lub Antek jest równe
A) 0,4 B) 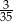 C) 0,02 D)
C) 0,02 D) 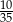
W konkursie biologicznym, w którym przewidziano tylko jedną nagrodę I stopnia, bierze udział 20 uczniów. Prawdopodobieństwo, że zwycięży Wojtek jest równe 0,30. Prawdopodobieństwo, że zwycięży Gosia jest równe 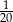 . Prawdopodobieństwo, że zwycięży Wojtek lub Gosia jest równe
. Prawdopodobieństwo, że zwycięży Wojtek lub Gosia jest równe
A) 0,25 B) 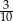 C) 0,35 D)
C) 0,35 D) 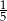
Punkty 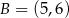 i
i 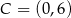 są wierzchołkami trapezu równoramiennego
są wierzchołkami trapezu równoramiennego 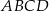 , którego podstawy
, którego podstawy 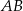 i
i 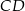 są prostopadłe do prostej
są prostopadłe do prostej 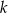 o równaniu
o równaniu 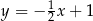 . Oblicz współrzędne pozostałych wierzchołków trapezu, wiedząc, że punkt
. Oblicz współrzędne pozostałych wierzchołków trapezu, wiedząc, że punkt 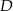 należy do prostej
należy do prostej 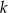 .
.
Suma pierwszego i szóstego wyrazu pewnego ciągu arytmetycznego jest równa 13 . Wynika stąd, że suma trzeciego i czwartego wyrazu tego ciągu jest równa
A) 13 B) 12 C) 7 D) 6
Suma pierwszego i siódmego wyrazu pewnego ciągu arytmetycznego jest równa 17 . Wynika stąd, że suma trzeciego i piątego wyrazu tego ciągu jest równa
A) 7 B) 16 C) 17 D) 6
Dany jest wielomian 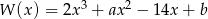 .
.
- Dla
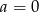 i
i 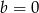 otrzymamy wielomian
otrzymamy wielomian 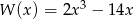 . Rozwiąż równanie
. Rozwiąż równanie 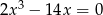 .
. - Dobierz wartości
 i
i 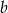 tak, aby wielomian
tak, aby wielomian 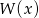 był podzielny jednocześnie przez
był podzielny jednocześnie przez 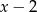 oraz
oraz 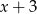 .
.
Dany jest równoległobok, którego boki zawierają się w prostych o równaniach: 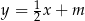 ,
, 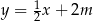 ,
, 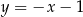 ,
, 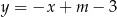 , gdzie
, gdzie 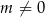 i
i 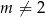 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 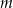 , dla których iloczyn długości dwóch wysokości tego równoległoboku, które nie są równoległe, jest równy
, dla których iloczyn długości dwóch wysokości tego równoległoboku, które nie są równoległe, jest równy 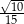 .
.
Funkcję kwadratową 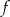 można opisać wzorem mającym postać
można opisać wzorem mającym postać 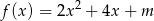 .
.
- Wyznacz warunek, dla którego funkcja
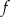 ma dwa różne pierwiastki
ma dwa różne pierwiastki 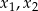 , a następnie oblicz
, a następnie oblicz 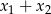 .
. - Wiedząc dodatkowo, że
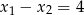 , oblicz
, oblicz 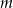 . Dla wyznaczonej liczby
. Dla wyznaczonej liczby 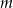 naszkicuj wykres funkcji
naszkicuj wykres funkcji 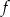 w układzie współrzędnych, a następnie rozwiąż równanie
w układzie współrzędnych, a następnie rozwiąż równanie 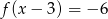 .
. 
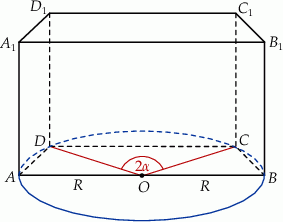
Podstawą graniastosłupa prostego 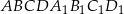 jest trapez równoramienny
jest trapez równoramienny 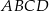 wpisany w okrąg o środku
wpisany w okrąg o środku 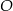 i promieniu
i promieniu 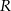 . Dłuższa podstawa
. Dłuższa podstawa 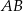 trapezu jest średnicą tego okręgu, a krótsza – cięciwą odpowiadającą kątowi środkowemu o mierze
trapezu jest średnicą tego okręgu, a krótsza – cięciwą odpowiadającą kątowi środkowemu o mierze 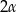 (zobacz rysunek). Przekątna ściany bocznej zawierającej ramię trapezu jest nachylona do płaszczyzny podstawy pod kątem o mierze
(zobacz rysunek). Przekątna ściany bocznej zawierającej ramię trapezu jest nachylona do płaszczyzny podstawy pod kątem o mierze  . Wyznacz objętość tego graniastosłupa jako funkcję promienia
. Wyznacz objętość tego graniastosłupa jako funkcję promienia 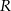 i miary kąta
i miary kąta  .
.
Punkt 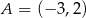 jest wierzchołkiem trójkąta równoramiennego
jest wierzchołkiem trójkąta równoramiennego 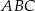 , w którym
, w którym 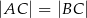 . Pole tego trójkąta jest równe 15. Bok
. Pole tego trójkąta jest równe 15. Bok 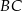 zawarty jest w prostej o równaniu
zawarty jest w prostej o równaniu 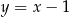 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 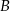 i
i 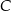 tego trójkąta.
tego trójkąta.
Punkt 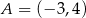 jest wierzchołkiem rozwartokątnego trójkąta równoramiennego
jest wierzchołkiem rozwartokątnego trójkąta równoramiennego 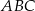 , w którym
, w którym 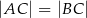 . Pole tego trójkąta jest równe 17,5 i wszystkie jego wierzchołki mają współrzędne całkowite. Bok
. Pole tego trójkąta jest równe 17,5 i wszystkie jego wierzchołki mają współrzędne całkowite. Bok 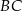 zawarty jest w prostej o równaniu
zawarty jest w prostej o równaniu 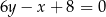 . Oblicz obwód trójkąta
. Oblicz obwód trójkąta 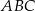 .
.
W trójkącie ostrokątnym 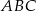 dane są
dane są 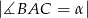 i
i 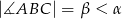 . Wykaż, że tangens kąta utworzonego przez środkową i wysokość opuszczone z wierzchołka
. Wykaż, że tangens kąta utworzonego przez środkową i wysokość opuszczone z wierzchołka 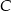 jest równy
jest równy
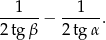
Funkcja kwadratowa 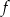 ma następujące własności:
ma następujące własności:
– zbiorem wartości funkcji 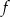 jest przedział
jest przedział 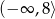 ;
;
– funkcja 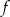 jest rosnąca w przedziale
jest rosnąca w przedziale 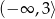 i malejąca w przedziale
i malejąca w przedziale 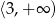 ;
;
– wykres funkcji 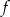 przecina oś
przecina oś 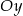 w punkcie, którego rzędna jest równa
w punkcie, którego rzędna jest równa 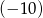 .
.
Wyznacz wzór funkcji 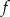 w postaci iloczynowej.
w postaci iloczynowej.
Egzamin składa się z 15 zadań zamkniętych. Do każdego zadania podano cztery odpowiedzi, z których tylko jedna okazuje się poprawna. Zdający zalicza egzamin, jeśli udzieli poprawnych odpowiedzi w co najmniej 11 zadaniach. Pewien student przystąpił nieprzygotowany do egzaminu i w każdym zadaniu wybierał losowo odpowiedź. Przyjmij, że w każdym zadaniu wybór każdej z odpowiedzi przez studenta jest równo prawdopodobny. Oblicz prawdopodobieństwo zdarzenia, że ten student zaliczył egzamin.
Doświadczenie losowe polega na trzykrotnym rzucie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia 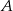 polegającego na tym, że w pierwszym rzucie otrzymamy parzystą liczbę oczek i iloczyn liczb oczek otrzymanych w trzech rzutach będzie podzielny przez 48.
polegającego na tym, że w pierwszym rzucie otrzymamy parzystą liczbę oczek i iloczyn liczb oczek otrzymanych w trzech rzutach będzie podzielny przez 48.
Siedmiokrotnie rzucamy kostką do gry. Wśród otrzymanych wyników jest 5 czwórek. Jakie jest prawdopodobieństwo, że w pierwszym rzucie otrzymaliśmy czwórkę?
Sześciokrotnie rzucamy kostką do gry. Wśród otrzymanych wyników są dokładnie trzy dwójki. Jakie jest prawdopodobieństwo, że w pierwszym rzucie otrzymaliśmy piątkę?
Dla jakich wartości parametru 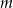 funkcja
funkcja
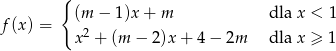
przyjmuje tylko dodatnie wartości?
Dany jest ciąg geometryczny
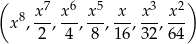
o wyrazach dodatnich. Wtedy
A) 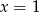 B)
B) 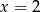 C)
C) 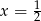 D)
D)