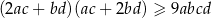Rozwiąż nierówność 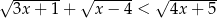 .
.
/Szkoła średnia/Nierówności
Wykaż, że istnieje liczba dodatnia  , dla której
, dla której 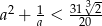 .
.
Udowodnij, że jeżeli 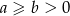 to
to 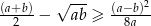 .
.
Wykaż, że dla dowolnych dodatnich liczb 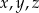 spełniona jest nierówność
spełniona jest nierówność
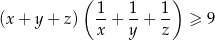
Uzasadnij, że jeżeli 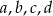 są liczbami dodatnimi to
są liczbami dodatnimi to
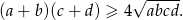
Rozwiąż nierówność 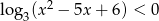 .
.
Rozwiąż nierówność 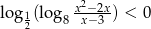 .
.
Wyznacz największą liczbę całkowitą spełniającą nierówność: 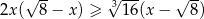 .
.
Wyznacz iloczyn (część wspólną) zbiorów rozwiązań nierówności: 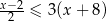 oraz
oraz 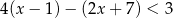 .
.
Wyznacz iloczyn (część wspólną) zbiorów rozwiązań nierówności: 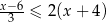 oraz
oraz 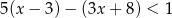 .
.
Wiedząc, że przedział 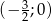 jest zbiorem wszystkich rozwiązań nierówności
jest zbiorem wszystkich rozwiązań nierówności 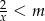 z niewiadomą
z niewiadomą  , oblicz
, oblicz 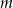 .
.
Rozwiąż nierówność 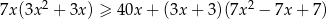 .
.
Udowodnij, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 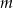 prawdziwa jest nierówność
prawdziwa jest nierówność 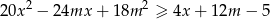 .
.
Udowodnij, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 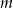 prawdziwa jest nierówność
prawdziwa jest nierówność 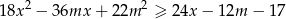 .
.
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 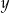 prawdziwa jest nierówność
prawdziwa jest nierówność 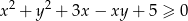 .
.
Udowodnij, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 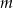 prawdziwa jest nierówność
prawdziwa jest nierówność 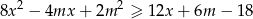 .
.
Wykaż, że dla dowolnych liczb rzeczywistych  i
i 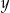 takich, że
takich, że 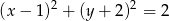 , prawdziwa jest nierówność
, prawdziwa jest nierówność 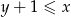 .
.
Rozwiąż nierówności i zaznacz na osi liczbowej liczby, które spełniają obie nierówności jednocześnie.
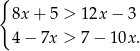
Rozwiąż nierówności i zaznacz na osi liczbowej liczby, które spełniają obie nierówności jednocześnie.
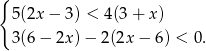
Rozwiąż nierówności i zaznacz na osi liczbowej liczby, które spełniają obie nierówności jednocześnie.
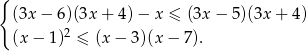
Rozwiąż nierówność 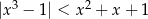 .
.
Wykaż, że dla dowolnej liczby rzeczywistej 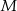 nierówność
nierówność
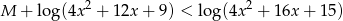
ma przynajmniej jedno rozwiązanie w przedziale 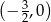 .
.
Zbiorem rozwiązań nierówności 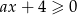 z niewiadomą
z niewiadomą  jest przedział
jest przedział 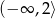 . Wyznacz
. Wyznacz  .
.
Zbiorem rozwiązań nierówności 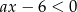 z niewiadomą
z niewiadomą  jest przedział
jest przedział 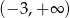 . Wyznacz
. Wyznacz  .
.
W układzie współrzędnych zaznacz rozwiązanie układu nierówności 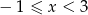 i
i 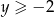 .
.
Wykaż, że dla dowolnych liczb rzeczywistych 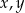 prawdziwa jest nierówność
prawdziwa jest nierówność
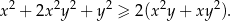
Wykaż, że dla dowolnych liczb rzeczywistych 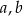 prawdziwa jest nierówność
prawdziwa jest nierówność