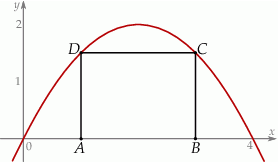
Rozpatrujemy wszystkie prostokąty 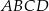 , których wierzchołki
, których wierzchołki 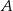 i
i 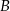 leżą na wykresie funkcji
leżą na wykresie funkcji 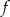 określonej wzorem
określonej wzorem 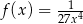 dla
dla 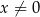 . Punkty
. Punkty 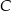 i
i 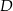 leżą na wykresie funkcji
leżą na wykresie funkcji 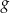 określonej wzorem
określonej wzorem 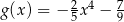 i są położone symetrycznie względem osi
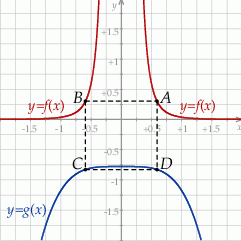
i są położone symetrycznie względem osi 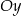 (zobacz rysunek). Oblicz współrzędne wierzchołka
(zobacz rysunek). Oblicz współrzędne wierzchołka 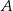 , dla którego pole prostokąta
, dla którego pole prostokąta 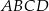 jest najmniejsze. Oblicz to najmniejsze pole.
jest najmniejsze. Oblicz to najmniejsze pole.

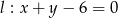 wyznacz taki punkt
wyznacz taki punkt 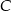 , aby długość łamanej
, aby długość łamanej 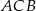 , gdzie
, gdzie 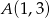 ,
, 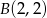 , była najmniejsza. Uzasadnij swoje rozumowanie.
, była najmniejsza. Uzasadnij swoje rozumowanie. 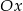 i paraboli o równaniu
i paraboli o równaniu 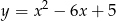 , a dwa należą do tej paraboli. Wyznacz współrzędne wierzchołków tego prostokąta, który ma największy obwód.
, a dwa należą do tej paraboli. Wyznacz współrzędne wierzchołków tego prostokąta, który ma największy obwód. 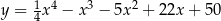 znajdź współrzędne punktu
znajdź współrzędne punktu 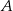 , którego odległość od prostej o równaniu
, którego odległość od prostej o równaniu 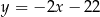 jest najmniejsza.
jest najmniejsza. 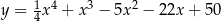 znajdź współrzędne punktu
znajdź współrzędne punktu 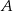 , którego odległość od prostej o równaniu
, którego odległość od prostej o równaniu 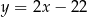 jest najmniejsza.
jest najmniejsza. 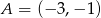 i
i 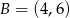 . Na wykresie funkcji
. Na wykresie funkcji 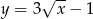 znajdź taki punkt
znajdź taki punkt 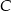 , dla którego pole trójkąta
, dla którego pole trójkąta 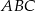 jest najmniejsze.
jest najmniejsze. 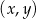 za pomocą fragmentów wykresów funkcji
za pomocą fragmentów wykresów funkcji 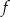 oraz
oraz 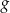 (zobacz rysunek).
(zobacz rysunek). 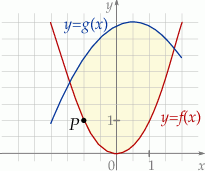
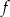 oraz
oraz 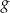 są określone wzorami
są określone wzorami 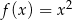 oraz
oraz 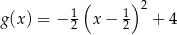 . Początek toru postanowiono zlokalizować na brzegu jeziora w miejscu, któremu odpowiada w układzie współrzędnych punkt
. Początek toru postanowiono zlokalizować na brzegu jeziora w miejscu, któremu odpowiada w układzie współrzędnych punkt 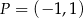 . Koniec toru regatowego należy umieścić na linii brzegowej. Oblicz współrzędne punktu
. Koniec toru regatowego należy umieścić na linii brzegowej. Oblicz współrzędne punktu 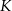 , w którym należy zlokalizować koniec toru, aby długość toru (tj. odległość końca
, w którym należy zlokalizować koniec toru, aby długość toru (tj. odległość końca 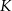 toru od początku
toru od początku 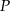 ) była możliwie największa. Oblicz długość najdłuższego toru.
) była możliwie największa. Oblicz długość najdłuższego toru. 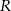 leżącego na wykresie funkcji
leżącego na wykresie funkcji 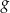 od punktu
od punktu 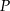 wyraża się wzorem
wyraża się wzorem 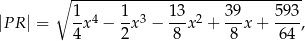
 jest pierwszą współrzędną punktu
jest pierwszą współrzędną punktu 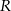 .
. 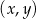 za pomocą fragmentów wykresów funkcji
za pomocą fragmentów wykresów funkcji 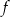 oraz
oraz 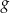 (zobacz rysunek).
(zobacz rysunek). 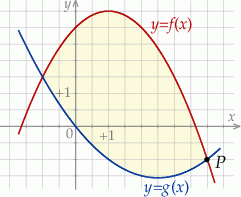
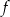 oraz
oraz 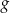 są określone wzorami
są określone wzorami 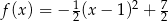 oraz
oraz 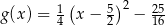 . Początek toru postanowiono zlokalizować na brzegu w miejscu, któremu odpowiada w układzie współrzędnych punkt
. Początek toru postanowiono zlokalizować na brzegu w miejscu, któremu odpowiada w układzie współrzędnych punkt 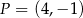 . Koniec toru regatowego należy umieścić na linii brzegowej. Oblicz współrzędne punktu
. Koniec toru regatowego należy umieścić na linii brzegowej. Oblicz współrzędne punktu 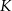 , w którym należy zlokalizować koniec toru, aby długość toru (tj. odległość końca
, w którym należy zlokalizować koniec toru, aby długość toru (tj. odległość końca 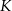 toru od początku
toru od początku 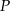 ) była możliwie największa. Oblicz długość najdłuższego toru.
) była możliwie największa. Oblicz długość najdłuższego toru. 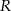 leżącego na wykresie funkcji
leżącego na wykresie funkcji 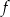 od punktu
od punktu 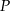 wyraża się wzorem
wyraża się wzorem 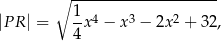
 jest pierwszą współrzędną punktu
jest pierwszą współrzędną punktu 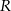 .
. 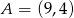 . Na okręgu o równaniu
. Na okręgu o równaniu 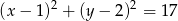 wyznacz współrzędne punktu
wyznacz współrzędne punktu 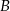 , dla którego odległość
, dla którego odległość 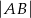 jest największa.
jest największa. 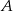 na prostej
na prostej 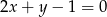 , by suma kwadratów jego odległości od osi układu była najmniejsza.
, by suma kwadratów jego odległości od osi układu była najmniejsza. 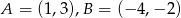 . Wyznacz taki punkt
. Wyznacz taki punkt 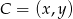 , gdzie
, gdzie 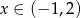 leżący na paraboli o równaniu
leżący na paraboli o równaniu 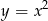 , aby pole trójkąta
, aby pole trójkąta 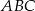 było największe.
było największe. 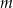 , dla której pole koła stycznego do prostych zawierających boki
, dla której pole koła stycznego do prostych zawierających boki 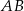 i
i 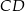 równoległoboku
równoległoboku 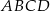 o wierzchołkach
o wierzchołkach 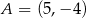 ,
, 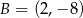 ,
, 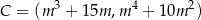 jest najmniejsze możliwe. Oblicz to pole.
jest najmniejsze możliwe. Oblicz to pole. 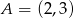 i
i 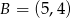 . Na prostej o równaniu
. Na prostej o równaniu 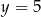 wyznacz punkt
wyznacz punkt 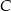 tak, aby łamana
tak, aby łamana 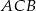 miała jak najmniejszą długość. Odpowiedź uzasadnij.
miała jak najmniejszą długość. Odpowiedź uzasadnij. 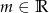 , dla których równanie
, dla których równanie 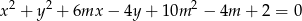
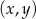 za pomocą fragmentów wykresów funkcji
za pomocą fragmentów wykresów funkcji 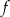 oraz
oraz 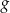 , które odpowiadają przeciwległym brzegom zbiornika (zobacz rysunek).
, które odpowiadają przeciwległym brzegom zbiornika (zobacz rysunek). 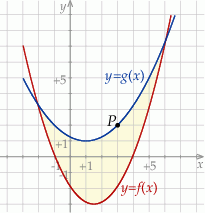
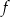 oraz
oraz 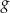 są określone wzorami
są określone wzorami 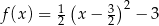 oraz
oraz 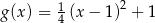 . Jeden z końców pomostu postanowiono zlokalizować na brzegu opisanym funkcją
. Jeden z końców pomostu postanowiono zlokalizować na brzegu opisanym funkcją 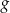 w punkcie o współrzędnych
w punkcie o współrzędnych 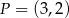 . Koniec pomostu należy umieścić na brzegu opisanym funkcją
. Koniec pomostu należy umieścić na brzegu opisanym funkcją 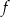 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 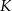 , w którym należy zlokalizować koniec pomostu, aby jego długość (tj. odległość końca
, w którym należy zlokalizować koniec pomostu, aby jego długość (tj. odległość końca 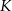 pomostu od początku
pomostu od początku 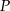 ) była możliwie najmniejsza. Oblicz długość najkrótszego pomostu.
) była możliwie najmniejsza. Oblicz długość najkrótszego pomostu. 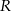 leżącego na wykresie funkcji
leżącego na wykresie funkcji 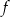 od punktu
od punktu 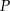 wyraża się wzorem
wyraża się wzorem 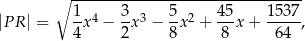
 jest pierwszą współrzędną punktu
jest pierwszą współrzędną punktu 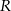 .
. 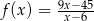 określonej dla
określonej dla 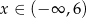 . Wykres ten przecina osie
. Wykres ten przecina osie 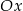 i
i 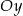 odpowiednio w punktach
odpowiednio w punktach 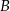 i
i 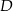 , a punkt
, a punkt 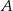 jest początkiem układu współrzędnych. Rozpatrujemy wszystkie czworokąty
jest początkiem układu współrzędnych. Rozpatrujemy wszystkie czworokąty 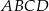 , w których punkt
, w których punkt 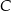 leży na wykresie funkcji
leży na wykresie funkcji 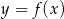 pomiędzy punktami
pomiędzy punktami 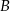 i
i 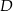 .
. 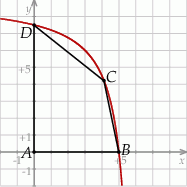
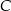 tego z rozpatrywanych czworokątów, którego pole jest największe.
tego z rozpatrywanych czworokątów, którego pole jest największe. 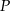 postaci:
postaci: 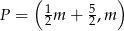 , gdzie
, gdzie 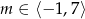 . Oblicz najmniejszą i największą wartość
. Oblicz najmniejszą i największą wartość 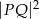 , gdzie
, gdzie 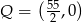 .
. 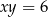 obrano punkty
obrano punkty 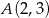 i
i 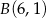 . Znajdź na tej krzywej taki punkt
. Znajdź na tej krzywej taki punkt 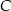 o ujemnej odciętej, aby pole trójkąta
o ujemnej odciętej, aby pole trójkąta 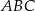 było najmniejsze.
było najmniejsze. 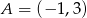 i
i 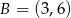 . Funkcja
. Funkcja 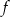 przyporządkowuje dowolnemu punktowi należącemu do odcinka
przyporządkowuje dowolnemu punktowi należącemu do odcinka 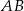 jego odległość od punktu
jego odległość od punktu 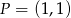 . Wyznacz zbiór wartości tej funkcji i jej wartość najmniejszą.
. Wyznacz zbiór wartości tej funkcji i jej wartość najmniejszą. 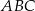 , których wierzchołki
, których wierzchołki 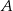 i
i 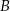 leżą na wykresie funkcji
leżą na wykresie funkcji 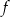 określonej wzorem
określonej wzorem 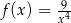 dla
dla 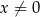 . Punkt
. Punkt 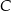 ma współrzędne
ma współrzędne 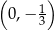 , a punkty
, a punkty 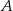 i
i 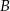 , są położone symetrycznie względem osi
, są położone symetrycznie względem osi 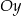 (zobacz rysunek). Oblicz współrzędne wierzchołków
(zobacz rysunek). Oblicz współrzędne wierzchołków 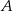 i
i 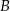 , dla których pole trójkąta
, dla których pole trójkąta 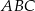 jest najmniejsze. Oblicz to najmniejsze pole.
jest najmniejsze. Oblicz to najmniejsze pole. 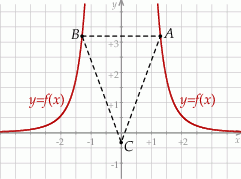
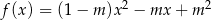 przecina oś
przecina oś 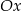 w punktach
w punktach 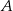 i
i 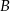 , które leżą po dwóch różnych stronach osi
, które leżą po dwóch różnych stronach osi 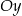 . Wyznacz tę wartość parametru
. Wyznacz tę wartość parametru 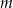 , dla której iloczyn odległości punktów
, dla której iloczyn odległości punktów 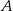 i
i 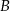 od początku układu współrzędnych jest najmniejszy możliwy. Dla wyznaczonej wartości
od początku układu współrzędnych jest najmniejszy możliwy. Dla wyznaczonej wartości 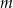 oblicz sumę odległości punktów
oblicz sumę odległości punktów 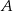 i
i 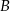 od początku układu współrzędnych.
od początku układu współrzędnych. 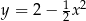 przecina oś
przecina oś 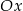 układu współrzędnych w punktach
układu współrzędnych w punktach 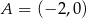 i
i 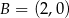 . Rozpatrujemy wszystkie trapezy równoramienne
. Rozpatrujemy wszystkie trapezy równoramienne 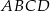 , których dłuższą podstawą jest odcinek
, których dłuższą podstawą jest odcinek 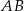 , a końce
, a końce 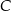 i
i 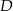 krótszej podstawy leżą na paraboli (zobacz rysunek).
krótszej podstawy leżą na paraboli (zobacz rysunek). 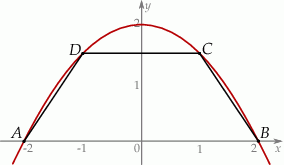
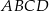 w zależności od pierwszej współrzędnej wierzchołka
w zależności od pierwszej współrzędnej wierzchołka 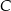 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 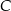 tego z rozpatrywanych trapezów, którego pole jest największe.
tego z rozpatrywanych trapezów, którego pole jest największe. 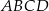 , których dwa wierzchołki
, których dwa wierzchołki 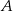 i
i 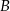 leżą na odcinku o końcach
leżą na odcinku o końcach 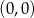 i
i 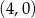 , a dwa pozostałe wierzchołki
, a dwa pozostałe wierzchołki 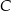 i
i 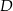 leżą na paraboli o równaniu
leżą na paraboli o równaniu 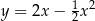 (zobacz rysunek).
(zobacz rysunek).