Zbadaj monotoniczność ciągu określonego wzorem 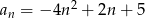 .
.
/Studia/Analiza/Ciągi/Monotoniczność
Zbadaj monotoniczność ciągu danego wzorem 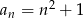 .
.
Zbadaj monotoniczność ciągu danego wzorem 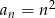 .
.
Zbadaj monotoniczność ciągu określonego wzorem 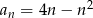 .
.
Zbadaj monotoniczność ciągu określonego wzorem 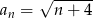 .
.
Ciąg 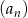 jest rosnący. Co można powiedzieć o monotoniczności ciągu
jest rosnący. Co można powiedzieć o monotoniczności ciągu 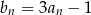 ?
?
Ciąg 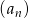 jest malejący. Co można powiedzieć o monotoniczność ciągu
jest malejący. Co można powiedzieć o monotoniczność ciągu 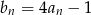 ?
?
Ciąg 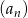 jest rosnący. Co można powiedzieć o monotoniczności ciągu
jest rosnący. Co można powiedzieć o monotoniczności ciągu 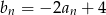 ?
?
Zbadaj monotoniczność ciągu 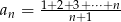 .
.
Ciąg 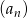 jest malejący i wszystkie jego wyrazy są dodatnie. Co można powiedzieć o monotoniczność ciągu
jest malejący i wszystkie jego wyrazy są dodatnie. Co można powiedzieć o monotoniczność ciągu 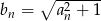 ?
?
Wyznacz te wartości parametru 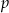 , dla których ciąg o wyrazie ogólnym
, dla których ciąg o wyrazie ogólnym 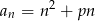 jest rosnący.
jest rosnący.
Dany jest ciąg o wyrazie ogólnym 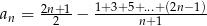 . Zbadaj monotoniczność tego ciągu i oblicz jego granicę.
. Zbadaj monotoniczność tego ciągu i oblicz jego granicę.
Zbadaj monotoniczność ciągu 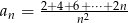 .
.
Zbadaj monotoniczność ciągu danego wzorem 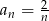 .
.
Zbadaj monotoniczność ciągu danego wzorem 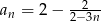 .
.
Zbadaj monotoniczność ciągu danego wzorem 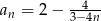 .
.
Ciąg 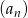 jest rosnący i wszystkie jego wyrazy są dodatnie. Co można powiedzieć o monotoniczności ciągu
jest rosnący i wszystkie jego wyrazy są dodatnie. Co można powiedzieć o monotoniczności ciągu 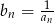 ?
?
Zbadaj monotoniczność ciągu określonego wzorem 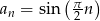 .
.
Zbadać, czy ciąg 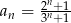 jest monotoniczny od pewnego miejsca.
jest monotoniczny od pewnego miejsca.
Zbadaj monotoniczność ciągu danego wzorem 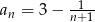 .
.
Zbadaj monotoniczność ciągu danego wzorem 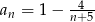 .
.
Zbadaj monotoniczność ciągu danego wzorem 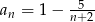 .
.
Zbadaj monotoniczność ciągu 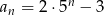 .
.
Ciąg 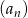 jest malejący i wszystkie jego wyrazy są dodatnie. Co można powiedzieć o monotoniczność ciągu
jest malejący i wszystkie jego wyrazy są dodatnie. Co można powiedzieć o monotoniczność ciągu 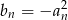 ?
?
Zbadaj monotoniczność ciągu danego wzorem 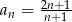 .
.
Zbadaj monotoniczność ciągu danego wzorem 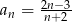 .
.
Zbadaj monotoniczność ciągu danego wzorem 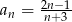 .
.
Zbadaj monotoniczność ciągu 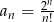 .
.

