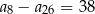Dany jest nieskończony ciąg geometryczny, w którym iloraz jest trzy razy większy od pierwszego wyrazu, a suma wszystkich wyrazów tego ciągu jest równa  . Pierwszy wyraz tego ciągu jest równy
. Pierwszy wyraz tego ciągu jest równy
A)  B)
B)  C)
C)  D) 7
D) 7
/Szkoła średnia/Zadania testowe/Ciągi
Dany jest nieskończony ciąg geometryczny, w którym iloraz jest trzy razy mniejszy od pierwszego wyrazu, a suma wszystkich wyrazów tego ciągu jest równa 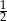 . Pierwszy wyraz tego ciągu jest równy
. Pierwszy wyraz tego ciągu jest równy
A) 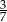 B)
B) 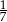 C)
C)  D) 7
D) 7
Miary kątów trójkąta tworzą ciąg arytmetyczny o pierwszym wyrazie 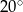 . Różnica tego ciągu jest równa
. Różnica tego ciągu jest równa
A) 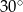 B)
B) 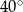 C)
C) 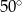 D)
D) 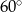
Miary kątów trójkąta tworzą ciąg arytmetyczny o pierwszym wyrazie 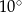 . Różnica tego ciągu jest równa
. Różnica tego ciągu jest równa
A) 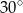 B)
B) 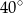 C)
C) 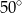 D)
D) 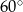
Miary kątów trójkąta tworzą ciąg arytmetyczny o pierwszym wyrazie 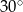 . Różnica tego ciągu jest równa
. Różnica tego ciągu jest równa
A) 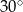 B)
B) 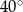 C)
C) 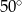 D)
D) 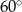
Granica 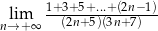 jest równa
jest równa
A) 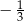 B)
B) 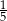 C)
C) 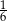 D) 0
D) 0
Dany jest ciąg 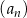 określony wzorem
określony wzorem 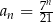 dla każdej liczby naturalnej
dla każdej liczby naturalnej 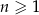 . Pięćdziesiątym wyrazem ciągu
. Pięćdziesiątym wyrazem ciągu 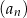 jest
jest
A) 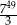 B)
B) 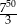 C)
C) 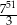 D)
D) 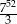
Ciąg 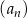 jest określony wzorem
jest określony wzorem 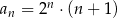 dla każdej liczby naturalnej
dla każdej liczby naturalnej 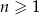 . Wyraz
. Wyraz 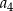 jest równy
jest równy
A) 64 B) 40 C) 48 D) 80
Miary kątów czworokąta tworzą ciąg geometryczny o ilorazie 2. Największy kąt tego czworokąta ma miarę
A) 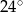 B)
B) 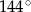 C)
C) 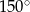 D)
D) 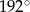
Miary kątów trójkąta tworzą ciąg geometryczny o ilorazie 4. Miara największego z nich jest równa
A) 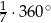 B)
B) 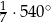 C)
C) 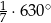 D)
D) 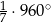
Ciąg 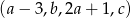 jest arytmetyczny i suma trzech jego początkowych wyrazów jest równa 78. Liczba
jest arytmetyczny i suma trzech jego początkowych wyrazów jest równa 78. Liczba  jest równa
jest równa
A) 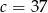 B)
B)  C)
C) 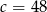 D)
D) 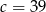
Suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 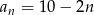 , gdzie
, gdzie 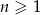 jest równa 14. Zatem
jest równa 14. Zatem
A) 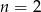 B) liczba
B) liczba 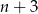 dzieli się przez 5 C)
dzieli się przez 5 C) 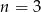 D)
D) 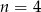
Suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 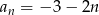 , gdzie
, gdzie 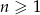 jest równa
jest równa 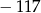 . Zatem
. Zatem
A) 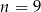 B)
B) 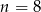 C)
C) 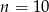 D)
D) 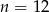
Liczby 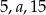 w tej kolejności tworzą ciąg arytmetyczny. Liczby
w tej kolejności tworzą ciąg arytmetyczny. Liczby 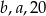 w tej kolejności tworzą ciąg geometryczny. Suma
w tej kolejności tworzą ciąg geometryczny. Suma 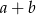 jest równa
jest równa
A) 20 B) 25 C) 15 D) 10
Liczby 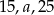 w tej kolejności tworzą ciąg arytmetyczny. Liczby
w tej kolejności tworzą ciąg arytmetyczny. Liczby 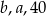 w tej kolejności tworzą ciąg geometryczny. Suma
w tej kolejności tworzą ciąg geometryczny. Suma 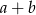 jest równa
jest równa
A) 40 B) 50 C) 20 D) 30
Liczby 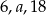 w tej kolejności tworzą ciąg arytmetyczny. Liczby
w tej kolejności tworzą ciąg arytmetyczny. Liczby 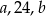 w tej kolejności tworzą ciąg geometryczny. Suma
w tej kolejności tworzą ciąg geometryczny. Suma 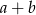 jest równa
jest równa
A) 60 B) 48 C) 12 D) 36
Dany jest ciąg geometryczny 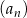 o wszystkich wyrazach niezerowych i pierwszym wyrazie
o wszystkich wyrazach niezerowych i pierwszym wyrazie 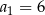 . Jeżeli
. Jeżeli 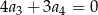 , to wzorem ogólnym ciągu
, to wzorem ogólnym ciągu 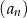 jest
jest
A) 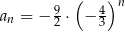 B)
B) 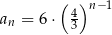 C)
C) 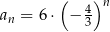 D)
D) 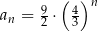
Dany jest ciąg geometryczny 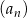 o wszystkich wyrazach niezerowych i pierwszym wyrazie
o wszystkich wyrazach niezerowych i pierwszym wyrazie 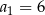 . Jeżeli
. Jeżeli 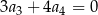 , to wzorem ogólnym ciągu
, to wzorem ogólnym ciągu 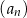 jest
jest
A) 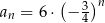 B)
B) 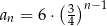 C)
C) 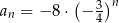 D)
D) 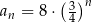
Dany jest ciąg geometryczny 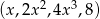 o wyrazach nieujemnych. Wtedy
o wyrazach nieujemnych. Wtedy
A) 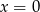 B)
B) 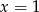 C)
C) 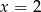 D)
D) 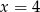
Dany jest ciąg geometryczny 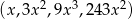 o wyrazach dodatnich. Wtedy
o wyrazach dodatnich. Wtedy
A) 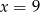 B)
B) 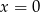 C)
C) 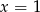 D)
D) 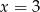
Dany jest ciąg geometryczny 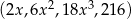 o wyrazach dodatnich. Wtedy
o wyrazach dodatnich. Wtedy
A) 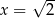 B)
B) 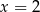 C)
C) 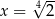 D)
D) 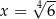
Suma dwóch początkowych wyrazów ciągu arytmetycznego 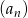 wynosi 5, a trzeci wyraz jest równy 7. Wówczas
wynosi 5, a trzeci wyraz jest równy 7. Wówczas
A) 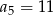 B)
B) 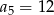 C)
C) 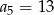 D)
D) 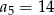
Suma dwóch początkowych wyrazów ciągu arytmetycznego 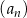 wynosi 7, a trzeci wyraz jest równy 5. Wówczas
wynosi 7, a trzeci wyraz jest równy 5. Wówczas
A) 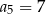 B)
B) 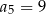 C)
C) 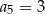 D)
D) 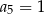
Ciąg 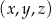 jest geometryczny. Iloczyn wszystkich wyrazów tego ciągu jest równy 64. Stąd wynika, że
jest geometryczny. Iloczyn wszystkich wyrazów tego ciągu jest równy 64. Stąd wynika, że 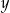 jest równe
jest równe
A) 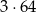 B)
B) 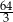 C) 4 D) 3
C) 4 D) 3
Ciąg 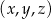 jest geometryczny. Iloczyn wszystkich wyrazów tego ciągu jest równy 27. Stąd wynika, że
jest geometryczny. Iloczyn wszystkich wyrazów tego ciągu jest równy 27. Stąd wynika, że 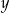 jest równe
jest równe
A) 81 B) 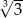 C) 9 D) 3
C) 9 D) 3
Dany jest ciąg o wyrazie ogólnym 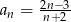 . Wynika stąd, że
. Wynika stąd, że
A) 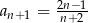 B)
B) 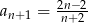 C)
C) 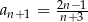 D)
D) 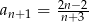
Dany jest ciąg o wyrazie ogólnym 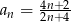 . Wynika stąd, że
. Wynika stąd, że
A) 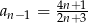 B)
B) 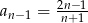 C)
C) 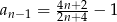 D)
D) 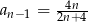
Ciąg 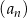 jest określony wzorem
jest określony wzorem 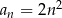 dla
dla 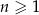 . Różnica
. Różnica 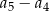 jest równa
jest równa
A) 4 B) 20 C) 36 D) 18
Ciąg 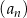 jest określony wzorem
jest określony wzorem 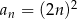 dla
dla 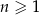 . Różnica
. Różnica 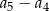 jest równa
jest równa
A) 4 B) 20 C) 36 D) 18
Iloczyn pierwszych 5 wyrazów ciągu geometrycznego danego wzorem 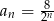 , gdzie
, gdzie 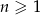 jest równy
jest równy
A) 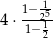 B)
B) 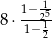 C)
C) 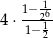 D)
D) 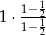
Iloczyn pierwszych 5 wyrazów ciągu geometrycznego danego wzorem 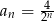 , gdzie
, gdzie 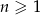 jest równy
jest równy
A) 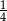 B)
B) 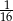 C)
C) 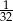 D)
D) 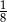
Suma ciągu arytmetycznego jest określona wzorem 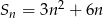 . Drugi wyraz tego ciągu jest równy
. Drugi wyraz tego ciągu jest równy
A) 24 B) 15 C) 6 D) 2
Suma ciągu arytmetycznego jest określona wzorem 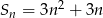 . Drugi wyraz tego ciągu jest równy
. Drugi wyraz tego ciągu jest równy
A) 18 B) 3 C) 12 D) 15
Suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 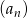 wyraża się wzorem
wyraża się wzorem 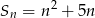 (
(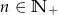 ). Drugi wyraz ciągu
). Drugi wyraz ciągu 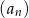 jest równy
jest równy
A) 2 B) 8 C) 12 D) 14
Dla każdej liczby całkowitej dodatniej  suma
suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 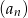 jest określona wzorem
jest określona wzorem 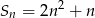 . Wtedy wyraz
. Wtedy wyraz 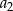 jest równy
jest równy
A) 3 B) 6 C) 7 D) 10
Jeśli suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 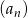 określona jest wzorem
określona jest wzorem 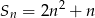 , to wartość trzeciego wyrazu tego ciągu jest równa
, to wartość trzeciego wyrazu tego ciągu jest równa
A) 8 B) 10 C) 11 D) 21
Suma częściowa ciągu arytmetycznego jest wyrażona wzorem 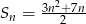 . Wobec tego:
. Wobec tego:
A) 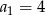 B)
B) 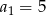 C)
C) 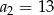 D)
D) 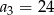
Suma ciągu arytmetycznego jest określona wzorem 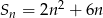 . Drugi wyraz tego ciągu jest równy
. Drugi wyraz tego ciągu jest równy
A) 20 B) 16 C) 12 D) 8
Jeżeli suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 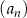 określona jest wzorem
określona jest wzorem 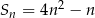 , to wartość piątego wyrazu tego ciągu jest równa
, to wartość piątego wyrazu tego ciągu jest równa
A) 33 B) 35 C) 60 D) 95
Dla każdej liczby całkowitej dodatniej  suma
suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 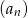 jest określona wzorem
jest określona wzorem 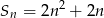 . Wtedy wyraz
. Wtedy wyraz 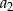 jest równy
jest równy
A) 4 B) 8 C) 12 D) 24
Nieskończony ciąg geometryczny 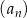 jest określony w następujący sposób:
jest określony w następujący sposób: 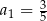 oraz
oraz 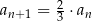 dla
dla 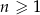 . Suma wszystkich wyrazów tego ciągu jest równa
. Suma wszystkich wyrazów tego ciągu jest równa
A)  B)
B) 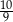 C)
C) 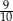 D)
D) 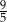
Nieskończony ciąg geometryczny 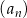 jest określony w następujący sposób:
jest określony w następujący sposób: 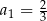 oraz
oraz 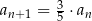 dla
dla 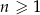 . Suma wszystkich wyrazów tego ciągu jest równa
. Suma wszystkich wyrazów tego ciągu jest równa
A)  B)
B) 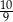 C)
C) 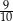 D)
D) 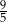
Jeżeli ciąg 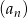 dany jest wzorem
dany jest wzorem 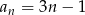 dla
dla 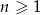 , to suma 10 początkowych wyrazów ciągu
, to suma 10 początkowych wyrazów ciągu 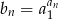 wyraża się wzorem
wyraża się wzorem
A) 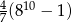 B)
B) 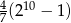 C)
C) 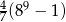 D)
D) 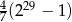
Ciąg 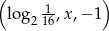 jest geometryczny. Wynika z tego, że
jest geometryczny. Wynika z tego, że
A) 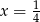 B)
B) 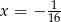 C)
C) 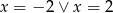 D)
D) 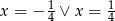
Ciąg 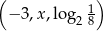 jest geometryczny. Wynika z tego, że
jest geometryczny. Wynika z tego, że
A) 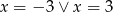 B)
B) 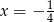 C)
C) 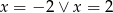 D)
D) 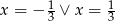
Ciąg 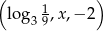 jest geometryczny. Wynika z tego, że
jest geometryczny. Wynika z tego, że
A) 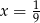 B)
B) 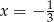 C)
C) 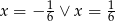 D)
D) 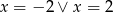
Ciąg arytmetyczny 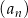 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 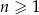 . Różnica tego ciągu jest równa 2. Wtedy
. Różnica tego ciągu jest równa 2. Wtedy
A) 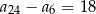 B)
B) 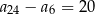 C)
C) 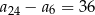 D)
D) 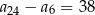
Ciąg arytmetyczny 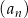 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 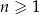 . Różnica tego ciągu jest równa
. Różnica tego ciągu jest równa 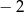 . Wtedy
. Wtedy
A) 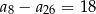 B)
B) 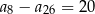 C)
C) 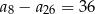 D)
D)